Auteur: Marc Fouchard
La loi de Planck montre que pour un corps noir, l'énergie émise par rayonnement suivant une longueur d'onde, ne dépend que de la température de surface du corps noir. Cette loi est donnée par la relation suivante :
: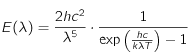
où 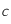 correspond à la vitesse de la lumière dans le vide,
correspond à la vitesse de la lumière dans le vide, 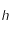 est la constante de Planck,
est la constante de Planck, 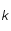 la constante de Boltzmann,
la constante de Boltzmann, 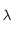 la longueur d'onde à laquelle le rayonnement est émis et
la longueur d'onde à laquelle le rayonnement est émis et 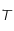 la température de surface du corps noir.
la température de surface du corps noir.
La figure ci dessous montre le comportement de 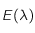 pour différente température de surface du corps noir. On peut remarquer que le maximum de la courbe se déplace sur la gauche lorsque la température augmente. Autrement dit, la longueur d'onde
pour différente température de surface du corps noir. On peut remarquer que le maximum de la courbe se déplace sur la gauche lorsque la température augmente. Autrement dit, la longueur d'onde 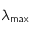 pour laquelle le rayonnement émis est maximal diminue lorsque la température de surface augmente.
pour laquelle le rayonnement émis est maximal diminue lorsque la température de surface augmente.
Loi de Planck 
Le but de cet exercice est de trouver la relation exacte entre 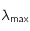 et
et 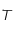 .
.
 Remarque
Remarque
Cette exercice repose sur la détermation du maximum d'une fonction sur un intervalle donné.
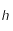 ,
, 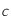 et
et 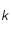 sont des constantes strictement positives et que la température
sont des constantes strictement positives et que la température 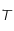 étant mesurée en degré Kelvin est aussi strictement positive, montrer que
étant mesurée en degré Kelvin est aussi strictement positive, montrer que 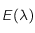 est de classe
est de classe 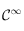 sur
sur ![]0,+\infty[](../pages_pt-fixe/equations_pt-fixe/equation17.png) et est toujours strictement positive sur cet intervalle.
et est toujours strictement positive sur cet intervalle.
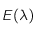 quand
quand 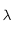 tend vers 0 et vers
tend vers 0 et vers 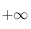 sont toutes les deux égales à zéro.
sont toutes les deux égales à zéro.
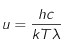 . Pour la limite en
. Pour la limite en 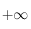 on pourra faire un dévelopement limité en 0 à l'ordre 1 de la fonction exponentielle.
on pourra faire un dévelopement limité en 0 à l'ordre 1 de la fonction exponentielle.
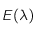 sur
sur 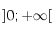 .
.
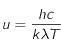 , montrer qu'étudier le signe de
, montrer qu'étudier le signe de 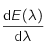 revient à étudier celui de
revient à étudier celui de 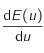 .
.
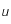 , de la forme
, de la forme 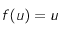 , pour que
, pour que 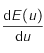 s'annule. On note
s'annule. On note 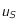 la solution de cette équation lorsqu'elle existe.
la solution de cette équation lorsqu'elle existe.
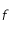 est une application contractante sur l'intervalle fermé
est une application contractante sur l'intervalle fermé 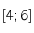 .
.
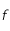 dans cet intervalle. Constuire une suite récurente convergent vers ce point fixe. En déduire une valeur
dans cet intervalle. Constuire une suite récurente convergent vers ce point fixe. En déduire une valeur 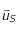 qui soit une valeur approchée de
qui soit une valeur approchée de 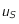 à
à 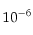 prêt.
prêt.
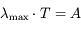 où
où 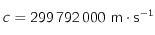 ,
, 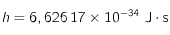 et
et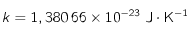 . Cette relation correspond à la loi de Wien pour les corps noirs.
Justifier l'utilisation de
. Cette relation correspond à la loi de Wien pour les corps noirs.
Justifier l'utilisation de 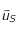 dans le calcul de la constante
dans le calcul de la constante 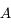 .
.
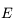 s'écrit comme un produit de fonctions ou composition de fonctions de classe
s'écrit comme un produit de fonctions ou composition de fonctions de classe 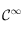 sur
sur ![]0,+\infty[](../pages_pt-fixe/equations_pt-fixe/equation20.png) , donc
, donc 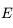 est aussi
est aussi 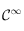 sur
sur ![]0,+\infty[](../pages_pt-fixe/equations_pt-fixe/equation23.png) . Et
. Et 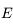 est strictement positive puisque chaque facteur apparaissant dans
est strictement positive puisque chaque facteur apparaissant dans 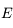 est strictement positif sur cet intervalle.
est strictement positif sur cet intervalle.
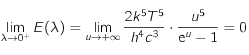 car l'exponentielle l'emporte sur tout polynôme en
car l'exponentielle l'emporte sur tout polynôme en 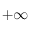 .
.
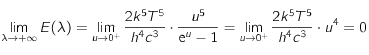 où on a utilisé le dévelopement limité en 0 à l'ordre 1 de la fonction exponentielle :
où on a utilisé le dévelopement limité en 0 à l'ordre 1 de la fonction exponentielle : 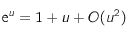 .
.
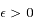 ,
, 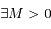 et
et 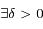 tels que
tels que 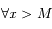 on a
on a 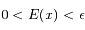 et
et 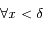 et
et 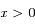 on a
on a 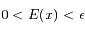 . Ainsi,
. Ainsi, 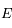 est une fonction continue sur l'intevalle
est une fonction continue sur l'intevalle ![[\delta,M]](../pages_pt-fixe/equations_pt-fixe/equation46.png) .
.
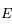 sur
sur ![[\delta,M]](../pages_pt-fixe/equations_pt-fixe/equation48.png) . Soit
. Soit 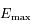 ce maximum. On peut toujours choisir
ce maximum. On peut toujours choisir 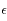 pour que
pour que 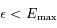 , ainsi
, ainsi 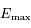 sera aussi le maximum de
sera aussi le maximum de 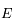 sur
sur ![]0,+\infty[](../pages_pt-fixe/equations_pt-fixe/equation54.png) .
.
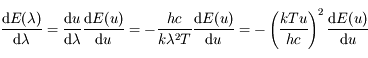 ce qui montre bien qu'étudier le signe de
ce qui montre bien qu'étudier le signe de 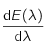 revient à étudier celui de
revient à étudier celui de 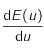 .
.
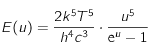 donc
donc 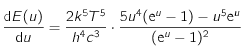 .
.
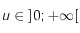 , et que
, et que 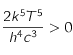 on a
on a 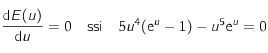 . Ainsi la condition sur
. Ainsi la condition sur 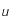 . peut se mettre sous la forme
. peut se mettre sous la forme 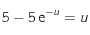 .
.
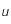 et
et 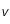 dans l'intervalle
dans l'intervalle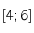 , on a
, on a 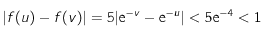 .
.
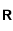 . La suite est simplement définie par
. La suite est simplement définie par 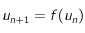 avec
avec ![u_0\in [ 4 ; 6]](../pages_pt-fixe/equations_pt-fixe/equation84.png) . Comme
. Comme 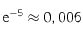 , on a
, on a 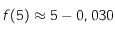 . On remarque que
. On remarque que 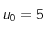 est un bon choix pour
est un bon choix pour 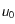 .
.