Détermination de la fraction continue (par la méthode d'approximation d'un réel décrite précédemment), des réduites (par la relation de récurrence) et de la stabilité (au bout de combien de temps, y a-t-il décalage d'un jour?):

\frac{p_0}{q_0} = [365]= 365 donne un décalage d'un jour en 4 ans.

\frac{p_1}{q_1} = [365;4]= 365+\frac{1}{4} donne un décalage d'un jour en 128 ans.

\frac{p_2}{q_2} = [365;4;7]= 365+\frac{7}{29} donne un décalage d'un jour en 1232 ans.

\frac{p_3}{q_3} = [365;4;7;1]= 365+\frac{8}{33} donne un décalage d'un jour en 4278 ans.

\frac{p_4}{q_4} = [365;4;7;1;3]= 365+\frac{31}{128} donne un décalage d'un jour en 331455 ans.

Ainsi, la réduite 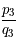\frac{p_3}{q_3} permet une meilleure approximation de l'année que l'année grégorienne mais la mise en place ne serait pas aisée pour un gain de stabilité d'un millénaire.

Par contre 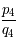\frac{p_4}{q_4} serait énormément plus interessant! Pour l'adopter, nous pouvons par exemple proposer de faire des années bissextiles les années multiples de quatre sauf les années multiples de 128 (pas évident à réaliser mais finalement peu contraignant au regard des 331455 ans de stabilité!).