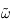 réel,
réel, 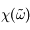 est défini comme la transformée de Fourier de G, elle est donc analytique.
est défini comme la transformée de Fourier de G, elle est donc analytique.
Pour 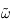 réel,
réel, 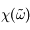 est défini comme la transformée de Fourier de G, elle est donc analytique.
est défini comme la transformée de Fourier de G, elle est donc analytique.
Pour tout t ≥ 0, 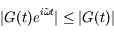 dans la partie supérieure du plan complexe (où
dans la partie supérieure du plan complexe (où 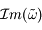 >0).
>0).
La définition assure que 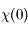 est fini, ce qui implique que
est fini, ce qui implique que 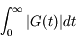 converge.
converge.
Ces deux dernières conditions assurent que 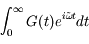 converge dans la partie supérieure du plan complexe.
converge dans la partie supérieure du plan complexe.