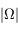 vers l'infini sur
vers l'infini sur 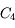 , et vers 0 sur
, et vers 0 sur 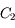 .
Le théorème de Cauchy assure que l'intégrale le long de ce contour est nulle :
.
Le théorème de Cauchy assure que l'intégrale le long de ce contour est nulle :
On utilise le contour suivant, en faisant tendre 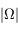 vers l'infini sur
vers l'infini sur 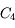 , et vers 0 sur
, et vers 0 sur 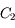 .
Le théorème de Cauchy assure que l'intégrale le long de ce contour est nulle :
.
Le théorème de Cauchy assure que l'intégrale le long de ce contour est nulle :
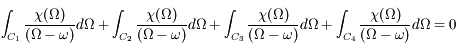
En appelant 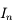 l'intégrale sur le contour
l'intégrale sur le contour 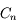 ,
, 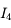 tend vers 0, la somme
tend vers 0, la somme 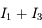 tend vers l'intégrale cherchée, et
tend vers l'intégrale cherchée, et 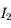 est donnée par le théorème de résidus. On a au total :
est donnée par le théorème de résidus. On a au total :
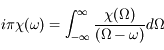
soit une relation entre 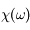 et son intégrale avec un coefficient imaginaire, ce qui implique une relation entre les parties réelle et imaginaire de
et son intégrale avec un coefficient imaginaire, ce qui implique une relation entre les parties réelle et imaginaire de 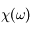 .
.