Auteur: Jérôme Thiébaut
L'un des outils les plus utilisés pour étudier le champ de densité de l'univers est le spectre de puissance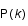 
. Ce spectre est relié à la transformée de Fourier de la fonction d'autocorrélation du champ et est une fonction des fréquences spatiales 
.
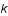En d'autres termes, la transformée de Fourier revient à effectuer un changement de base et à remplacer le champ 
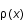définie de manière locale par une somme de sinusoides, 
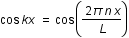contenues dans une boîte de taille L, définissant le champ de manière globale.
Ainsi, le spectre de puissance donne pour chaque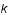 
, le poids de cette fréquence.
Dans la jeunesse de l'univers, celui ci était invariant d'échelle, ce qui signifie qu'il n'existait aucune longueur caractéristiques ou privilégiée. Ainsi le spectre était une loi de puissance de la forme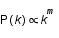 
. On voit que la connaissance d'une seule quantité, l'indice 
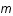, procure beaucoup d'information. Le spectre de puissance est donc un outil très puissant et est extrêmement utilisé en cosmologie, notamment dans les simulations numériques.
Le but de cet exercice est de relier de manière précise le spectre de puissance à la transformée de Fourier de la fonction d'autocorrélation du champ de densité.
spectre de puissance
Introduction
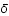par 
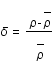, où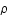 
est la densité et 
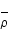la densité moyenne.
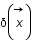comme une série de Fourier:
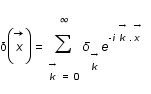, où le vecteur 
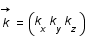est tel que 
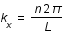avec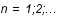 
.De même pour 
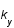et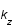 
.
,
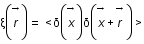où la valeur moyenne s'effectue sur le volume de la boîte.
.
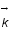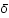étant réel, les coefficients 
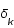obéissent à la relation de conjugaison 
.
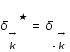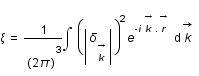, où le facteur 
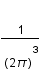a été introduit par commodité. On définit le spectre de puissance comme : 
.
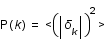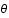et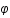 
) et exprimer le résultat en fonction du spectre de puissance. Si on inverse cette relation, on trouve que 
.
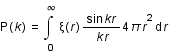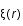étant une fonction réelle, 
.
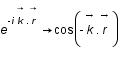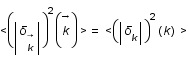où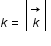 
.
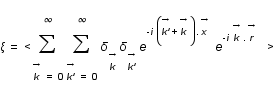
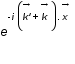s'annule en moyenne sauf pour 
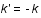. Il reste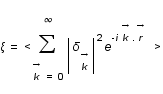 
.
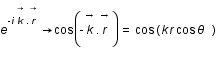
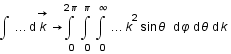
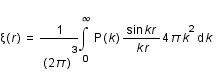