 Relation de dispersion
Relation de dispersion
Difficulté : ☆☆ Temps : 1h
Un plasma est constitué d'ions et d'électrons. Les ions étant largement plus lourds, nous allons les supposer immobiles dans le développement qui suit. Considérons qu'ils sont répartis uniformément dans l'espace avec une densité 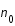 .
.
L'onde de Langmuir étant la propagation d'une perturbation électrostatique (écart à la neutralité mais sans création de courant électrique à grande échelle), nous pouvons, pour simplifier le problème, supposer l'absence de champ magnétique.
A l'équilibre, les électrons sont eux aussi immobiles et uniformément répartis avec une densité 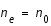 . Mais, que se passe t-il si on perturbe cet équilibre en posant que
. Mais, que se passe t-il si on perturbe cet équilibre en posant que 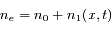 , où
, où 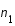 est un petit terme perturbatif qui dépend de la position
est un petit terme perturbatif qui dépend de la position 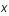 et du temps
et du temps 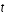 ?
?
Dans ce cas, un champ électrique 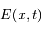 se crée et met les électrons en mouvement à une vitesse
se crée et met les électrons en mouvement à une vitesse 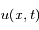 .
.
Les équations qui gouvernent ensuite l'évolution de ces trois grandeurs (perturbation de densité, champ électrique et vitesse des électrons) sont l'équation de continuité, l'équation de conservation du moment dynamique et l'équation de Poisson:
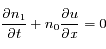
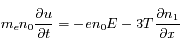
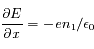
où 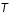 est la température moyenne des électrons,
est la température moyenne des électrons, 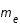 leur masse,
leur masse, 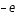 leur charge, et
leur charge, et 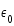 la permittivité du vide.
la permittivité du vide.
Les équations ont été ici écrites à une dimension, dans la direction x. On suppose que les perturbations vont se propager dans cette direction sous la forme d'onde plane et donc que l'on peut écrire:
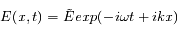
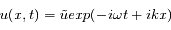
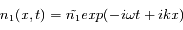
où 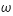 est la pulsation de l'onde et
est la pulsation de l'onde et 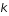 l'amplitude de son vecteur d'onde selon
l'amplitude de son vecteur d'onde selon 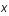 .
.
Écrire le système linéaire vérifié par les inconnues 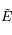 ,
, 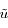 et
et 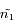 et ayant
et ayant 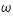 et
et 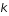 comme paramètres.
comme paramètres.
Trouver la relation de dispersion de l'onde, c'est à dire une expression de 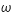 en fonction de
en fonction de 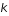 .
.
Si on prend le mouvement des ions en compte, le système d'équation change et on trouve une nouvelle relation de dispersion qui correspond cette fois à une onde acoustique ionique.
En utilisant la même méthode que précédemment, retrouver la fonction de dispersion d'une onde acoustique ionique à partir du système d'équations ci dessous. Les indices 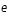 et
et  indiquent l'espèce (électron ou ion).
indiquent l'espèce (électron ou ion).
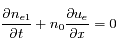
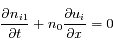
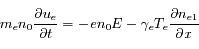
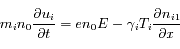
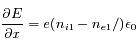
où les 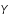 sont des constantes (rapports des chaleurs spécifiques de chaque espèce).
sont des constantes (rapports des chaleurs spécifiques de chaque espèce).
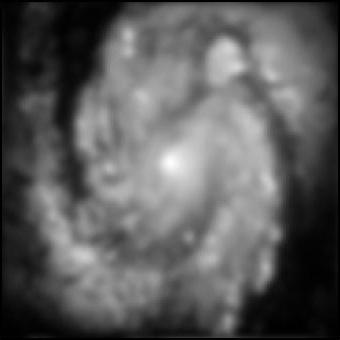
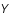 . Ce vecteur resulte de l'image initiale,
. Ce vecteur resulte de l'image initiale, 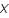 , qui a été convoluée par le télescope auquel s'ajoute un vecteur bruit noté
, qui a été convoluée par le télescope auquel s'ajoute un vecteur bruit noté 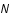 .
La convolution se modélise par l'application d'une matrice
.
La convolution se modélise par l'application d'une matrice 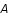 sur le vecteur
sur le vecteur 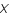 . Ainsi on a:
. Ainsi on a:
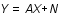 .
Dans l'espace de Fourier, cette relation s'ecrit:
.
Dans l'espace de Fourier, cette relation s'ecrit: 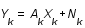 où
où 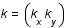 représente la fréquence spatiale en deux dimensions. Dans cet espace, la matrice
représente la fréquence spatiale en deux dimensions. Dans cet espace, la matrice 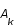 est diagonale de valeur propre
est diagonale de valeur propre 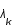 .
Le spectre de puissance de l'image suit souvent une loi de puissance, c'est à dire
.
Le spectre de puissance de l'image suit souvent une loi de puissance, c'est à dire 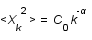 et le bruit est souvent un bruit blanc c'est à dire qu'il à la même intensité quelquesoit la fréquence spatiale,
et le bruit est souvent un bruit blanc c'est à dire qu'il à la même intensité quelquesoit la fréquence spatiale, 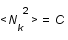 , où
, où 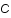 et
et 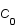 sont des constantes.
Montrer que l'inversion simple de cette relation (qui consiste à appliquer la matrice
sont des constantes.
Montrer que l'inversion simple de cette relation (qui consiste à appliquer la matrice 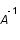 sur les données
sur les données 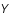 afin de retrouver
afin de retrouver 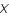 ) conduit, au delà d'une certaine fréquence, à une amplification du bruit.
) conduit, au delà d'une certaine fréquence, à une amplification du bruit.

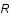 à appliquer sur les données
à appliquer sur les données 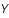 qui va minimiser l'écart quadratique moyen entre la vraie image
qui va minimiser l'écart quadratique moyen entre la vraie image 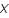 et l'image filtrée
et l'image filtrée 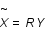 . On cherche donc à minimiser la quantité
. On cherche donc à minimiser la quantité 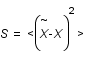 par rapport à
par rapport à 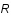 . En postulant que le bruit et le signal sont décorrélés et que le bruit est non biaisé (pas d'erreur systématique), montrer que
. En postulant que le bruit et le signal sont décorrélés et que le bruit est non biaisé (pas d'erreur systématique), montrer que 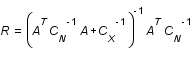 ,où
,où 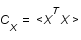 et
et 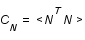 sont les matrices de variance-covariance du signal et du bruit.
sont les matrices de variance-covariance du signal et du bruit.
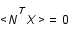 ou tout autre produit de ce genre. Si les données sont non biaisées,
ou tout autre produit de ce genre. Si les données sont non biaisées, 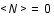 .
.
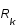 inverse les basses fréquences et coupe les plus grandes où le bruit domine.
inverse les basses fréquences et coupe les plus grandes où le bruit domine.
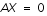 avec:
avec:
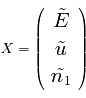 et
et 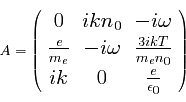
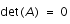 donne la relation de dispersion suivante:
donne la relation de dispersion suivante:
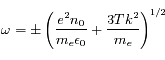
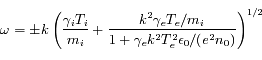
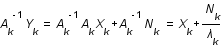 . Comme le spectre de puissance de l'image decroit quand
. Comme le spectre de puissance de l'image decroit quand 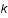 augmente et que celui du bruit reste constant, il existe une fréquence limite
augmente et que celui du bruit reste constant, il existe une fréquence limite 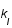 à partir delaquelle
à partir delaquelle 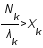 et donc le bruit est amplifié et domine la reconstruction de l'image.
et donc le bruit est amplifié et domine la reconstruction de l'image.

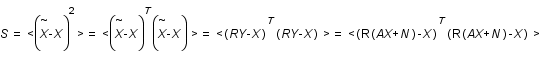 .
Minimiser
.
Minimiser 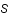 par rapport à
par rapport à 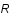 revient à resoudre
revient à resoudre 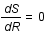 . Ceci conduit à
. Ceci conduit à 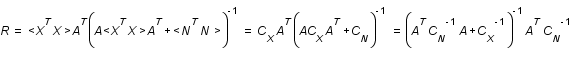
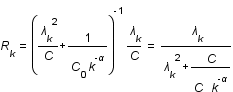 donc à petit
donc à petit 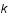 ,
, 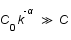 et
et 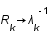 et à grand
et à grand 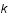 ,
, 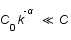 et
et 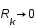 .
Les très hautes fréquences dominées par le bruit sont coupées, l'image est donc filtrée.
.
Les très hautes fréquences dominées par le bruit sont coupées, l'image est donc filtrée.