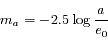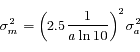Mesurer une quantité physique, c'est faire une estimation de la valeur de cette quantité. Cette estimation peut être entachée de deux types d'erreurs : erreur systématique, et erreur aléatoire. La première est liée à l'instrument de mesure ou au type d'observation (si on mesure plusieurs phénomènes simultanément sans s'en rendre compte), elle peut être additive (niveau de base ou offset, par exemple le courant d'obscurité d'une caméra) ou multiplicative (réglage de gain défectueux). Les erreurs aléatoires sont liées au processus de mesure lui-même (bruit de lecture) ou à la nature du phénomène mesuré (bruit de photon d'une source lumineuse faible, lié au processus d'émission). Une bonne mesure est telle que les erreurs aléatoires sont minimisées, et que les erreurs systématiques sont beaucoup plus petites que celles-ci.
L'exercice consiste à dériver la meilleure estimation de l'éclairement d'un corps céleste, dans l'hypothèse où l'erreur systématique est faible.
Auteur: Stéphane Erard
 Estimation d'une moyenne
Estimation d'une moyenne
Difficulté : ☆
Temps : 30 min
On mesure l'éclairement d'une étoile. La valeur "réelle" est notée  (celle que mesurerait un instrument parfait).
(celle que mesurerait un instrument parfait).
Pour obtenir une bonne estimation de cette quantité, une méthode usuelle est de pratiquer N mesures successives  . On s'attend à ce que celles-ci se répartissent de façon gaussienne autour de la valeur
. On s'attend à ce que celles-ci se répartissent de façon gaussienne autour de la valeur 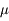 (théorème de la limite centrale).
(théorème de la limite centrale).
Question 1)
A partir de ces N estimations indépendantes de l'éclairement, dériver le résultat de la mesure : valeur estimée de la moyenne 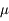 , et incertitude sur cette estimation.
, et incertitude sur cette estimation.
Question 2)
Plusieurs équipes ayant publié leurs résultats (maintenant notés 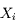 ), on veut en tirer la meilleure évaluation possible. Ce problème est équivalent à celui de mesures successives entachées d'incertitudes indépendantes
), on veut en tirer la meilleure évaluation possible. Ce problème est équivalent à celui de mesures successives entachées d'incertitudes indépendantes 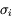 .
.
Application numérique : on a deux mesures indépendantes 100±5 et 94±20. Quelle est l'estimation résultante ?
On s'intéresse souvent à une fonction des quantités mesurées. Le problème est alors de dériver l'incertitude associée à cette estimation.
C'est par exemple le cas en spectroscopie, où on mesure une intensité 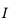 à diverses longueurs d'onde
à diverses longueurs d'onde 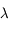 (variable indépendante). Les quantités physiquement importantes sont liées aux variations spectrales ; elles s'expriment comme des différences ou des rapports d'intensités à différentes longueurs d'onde, ou comme des fonctions plus complexes de ces intensités. Une incertitude individuelle est associée à chaque mesure spectrale
(variable indépendante). Les quantités physiquement importantes sont liées aux variations spectrales ; elles s'expriment comme des différences ou des rapports d'intensités à différentes longueurs d'onde, ou comme des fonctions plus complexes de ces intensités. Une incertitude individuelle est associée à chaque mesure spectrale 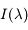 . En principe, les incertitudes sur les mesures individuelles sont indépendantes les unes des autres. Si ce n'est pas le cas, il y a un problème avec l'étalonnage de l'instrument et il faut ajouter un terme de covariance dans les formules ci-dessous (on parle improprement de « bruit corrélé », parce qu'un signal inconnu se superpose à celui qu'on mesure).
. En principe, les incertitudes sur les mesures individuelles sont indépendantes les unes des autres. Si ce n'est pas le cas, il y a un problème avec l'étalonnage de l'instrument et il faut ajouter un terme de covariance dans les formules ci-dessous (on parle improprement de « bruit corrélé », parce qu'un signal inconnu se superpose à celui qu'on mesure).
 Erreurs sur une fonction
Erreurs sur une fonction
Difficulté : ☆☆
Temps : 30 min
 Introduction
Introduction
L'exercice consiste à dériver la précision des estimations de différentes fonctions spectrales.
Question 1)
La fonction est une combinaison additive de variables :
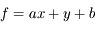
où a et b sont des constantes, et x et y sont affectées des incertitudes 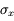 et
et 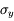 .
.
Quelle est l'incertitude associée 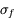 ?
?
Question 2)
On utilise maintenant une fonction multiplicative :
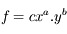 où a, b et c sont des constantes.
où a, b et c sont des constantes.
Quelle est l'incertitude associée 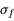 ?
?
Question 3)
Pour les cas plus compliqués où l'on connaît la forme analytique de la fonction, écrire la formulation générale.
Question 4)
On applique ces résultats à la situation suivante :
On mesure les intensités a, b et c aux longueurs d'onde 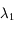 ,
, 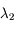 et
et 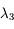 situées autour d'une bande d'absorption, avec les incertitudes
situées autour d'une bande d'absorption, avec les incertitudes 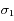 ,
, 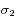 et
et 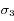 .
.
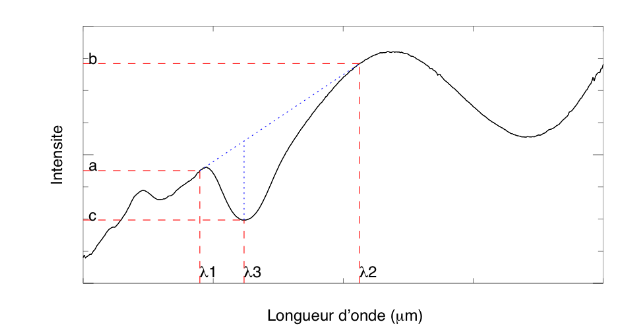
Exemple de spectre infrarouge et définition des paramètres mesurés
On estime le continuum (pente spectrale) autour de la bande d'absorption comme 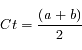
et la profondeur de cette bande comme 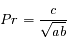
Écrire les incertitudes sur ces quantités en fonction de celles des mesures.
Question 5)
On utilise maintenant la mesure d'éclairement 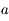 pour estimer la magnitude à la longueur d'onde
pour estimer la magnitude à la longueur d'onde 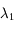 .
.
Ecrire cette magnitude en fonction de 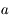 et d'une constante d'échelle.
et d'une constante d'échelle.
Question 6)
Ecrire l'incertitude sur cette magnitude en fonction de celle sur l'éclairement.
-
Question 1
Solution :
Le meilleur estimateur de l'éclairement de la source est la moyenne des mesures :
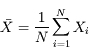
L'écart-type σ donne la dispersion des mesures :
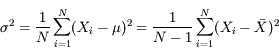
Le facteur N / (N-1) provient du fait qu'on doit utiliser dans le calcul un estimateur de la moyenne plutôt que la moyenne elle-même, et corrige du biais ainsi introduit.
La précision sur l'estimateur de la moyenne est l'erreur-type :
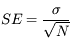
Le résultat est donc 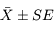 . En pratique, on peut utiliser
. En pratique, on peut utiliser 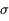 comme barre d'erreur "réaliste" sur le résultat pour éviter toute sur-interprétation.
comme barre d'erreur "réaliste" sur le résultat pour éviter toute sur-interprétation.
-
Question 2
Solution :
Le meilleur estimateur de l'éclairement est la moyenne des mesures pondérées par leurs incertitudes :
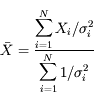
L'incertitude globale est :
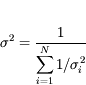
Elle est normalement égale à l'erreur-type. Si ce n'est pas le cas, cela indique qu'on a probablement négligé une erreur systématique.
Application numérique : la meilleure estimation est 100±5 (en conservant la précision des données d'origine). La moyenne arithmétique naïve (sans pondération par l'incertitude) 97±10 est particulièrement trompeuse dans ce cas : l'incertitude sur la deuxième mesure est ici si grande qu'elle ne contribue pas au résultat, mais ne le dégrade pas non plus.
 Estimation d'une moyenne
Estimation d'une moyenne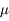 (celle que mesurerait un instrument parfait).
(celle que mesurerait un instrument parfait).
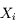 . On s'attend à ce que celles-ci se répartissent de façon gaussienne autour de la valeur
. On s'attend à ce que celles-ci se répartissent de façon gaussienne autour de la valeur 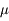 (théorème de la limite centrale).
(théorème de la limite centrale).
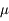 , et incertitude sur cette estimation.
, et incertitude sur cette estimation.
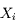 ), on veut en tirer la meilleure évaluation possible. Ce problème est équivalent à celui de mesures successives entachées d'incertitudes indépendantes
), on veut en tirer la meilleure évaluation possible. Ce problème est équivalent à celui de mesures successives entachées d'incertitudes indépendantes 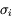 .
.
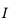 à diverses longueurs d'onde
à diverses longueurs d'onde 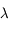 (variable indépendante). Les quantités physiquement importantes sont liées aux variations spectrales ; elles s'expriment comme des différences ou des rapports d'intensités à différentes longueurs d'onde, ou comme des fonctions plus complexes de ces intensités. Une incertitude individuelle est associée à chaque mesure spectrale
(variable indépendante). Les quantités physiquement importantes sont liées aux variations spectrales ; elles s'expriment comme des différences ou des rapports d'intensités à différentes longueurs d'onde, ou comme des fonctions plus complexes de ces intensités. Une incertitude individuelle est associée à chaque mesure spectrale 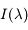 . En principe, les incertitudes sur les mesures individuelles sont indépendantes les unes des autres. Si ce n'est pas le cas, il y a un problème avec l'étalonnage de l'instrument et il faut ajouter un terme de covariance dans les formules ci-dessous (on parle improprement de « bruit corrélé », parce qu'un signal inconnu se superpose à celui qu'on mesure).
. En principe, les incertitudes sur les mesures individuelles sont indépendantes les unes des autres. Si ce n'est pas le cas, il y a un problème avec l'étalonnage de l'instrument et il faut ajouter un terme de covariance dans les formules ci-dessous (on parle improprement de « bruit corrélé », parce qu'un signal inconnu se superpose à celui qu'on mesure).
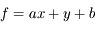
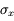 et
et 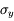 .
.
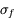 ?
?
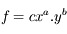 où a, b et c sont des constantes.
où a, b et c sont des constantes.
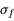 ?
?
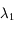 ,
, 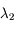 et
et 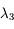 situées autour d'une bande d'absorption, avec les incertitudes
situées autour d'une bande d'absorption, avec les incertitudes 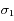 ,
, 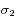 et
et 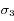 .
.

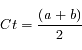
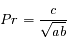
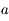 pour estimer la
pour estimer la 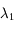 .
.
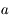 et d'une constante d'échelle.
et d'une constante d'échelle.
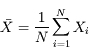
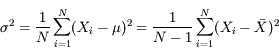
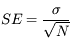
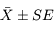 . En pratique, on peut utiliser
. En pratique, on peut utiliser 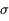 comme barre d'erreur "réaliste" sur le résultat pour éviter toute sur-interprétation.
comme barre d'erreur "réaliste" sur le résultat pour éviter toute sur-interprétation.
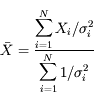
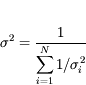
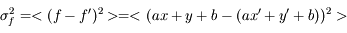
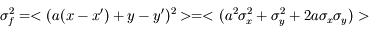
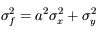 si les erreurs sont indépendantes.
si les erreurs sont indépendantes.
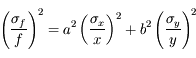
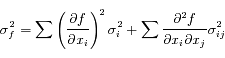
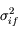 est la covariance de
est la covariance de 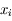 et
et 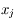 , qu'on néglige habituellement (en faisant l'hypothèse que les mesures sont décorrélées).
, qu'on néglige habituellement (en faisant l'hypothèse que les mesures sont décorrélées).
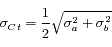
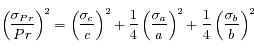
 étant un éclairement (ou irradiance), en notant
étant un éclairement (ou irradiance), en notant 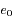 l'éclairement qui correspond à la magnitude 0, on a :
l'éclairement qui correspond à la magnitude 0, on a :