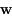 , si on note
, si on note 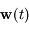 et
et 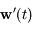 les évolutions respectives de
les évolutions respectives de 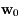 et
et 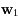 on a:
on a:
Toujours du fait de la linéarité de l'équation différentielle décrivant l'évolution de 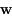 , si on note
, si on note 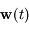 et
et 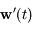 les évolutions respectives de
les évolutions respectives de 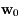 et
et 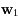 on a:
on a:
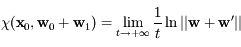 .
.
D'après l'inégalité de Cauchy-Schwarz on a: 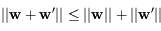 . Ainsi, la fonction logarithme étant croissante, on a:
. Ainsi, la fonction logarithme étant croissante, on a:
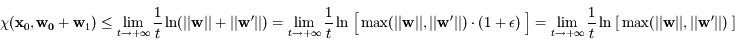
où 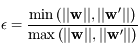 , ainsi
, ainsi 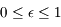 ce qui permet d'éliminer le facteur
ce qui permet d'éliminer le facteur 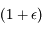 lors du passage à la limite (division par
lors du passage à la limite (division par  ).
).
Lorsque les limites existent on a:
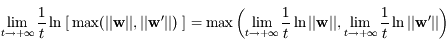 ,
,
Ce qui montre le résultat.