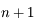 . soit
. soit 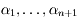 les
les 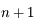 exposants de Lyapunov, tels que
exposants de Lyapunov, tels que 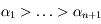 . Par définition on a
. Par définition on a 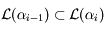 avec
avec 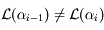 .
Ainsi
.
Ainsi 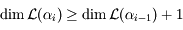 . Soit
. Soit 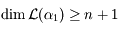 . Or
. Or 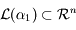 qui est de dimension
qui est de dimension 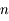 , donc il ne peut y avoir
, donc il ne peut y avoir 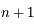 exposants de Lyapunov distincts.
exposants de Lyapunov distincts.
Supposons qu'il en existe 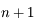 . soit
. soit 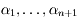 les
les 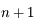 exposants de Lyapunov, tels que
exposants de Lyapunov, tels que 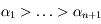 . Par définition on a
. Par définition on a 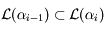 avec
avec 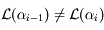 .
Ainsi
.
Ainsi 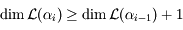 . Soit
. Soit 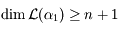 . Or
. Or 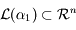 qui est de dimension
qui est de dimension 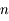 , donc il ne peut y avoir
, donc il ne peut y avoir 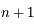 exposants de Lyapunov distincts.
exposants de Lyapunov distincts.