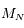 est antisymétrique, son rang est pair. C'est un résultat classique d'algèbre linéaire, non redémontré ici.
est antisymétrique, son rang est pair. C'est un résultat classique d'algèbre linéaire, non redémontré ici.
Puisque 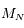 est antisymétrique, son rang est pair. C'est un résultat classique d'algèbre linéaire, non redémontré ici.
est antisymétrique, son rang est pair. C'est un résultat classique d'algèbre linéaire, non redémontré ici.
Par conséquent, pour des angles 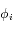 donnés, l'existence de solutions non-triviales (positives ou négatives) du système linéaire va dépendre de la parité du nombre
donnés, l'existence de solutions non-triviales (positives ou négatives) du système linéaire va dépendre de la parité du nombre 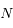 de satellites.
de satellites.
Si N est impair, 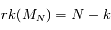 avec
avec 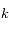 impair. Ainsi, étant données des séparations angulaires arbitraires et non-nulles entre les satellites, il existe une famille à k paramètres de vecteurs
impair. Ainsi, étant données des séparations angulaires arbitraires et non-nulles entre les satellites, il existe une famille à k paramètres de vecteurs 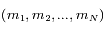 pour laquelle la configuration est stationnaire: étant données par exemple
pour laquelle la configuration est stationnaire: étant données par exemple 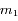 ,
, 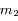 , ...,
, ..., 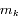 , le système linéaire admet une et une seule solution
, le système linéaire admet une et une seule solution 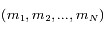 .
.
Notons cependant que les masses doivent être positives pour que la solution correspondante ait un sens physique. Cela réduit les configurations angulaires possibles 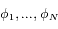 à un sous-ensemble de
à un sous-ensemble de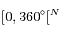 .
.
En fait 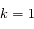 "presque partout". Dans l'espace des
"presque partout". Dans l'espace des 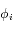 , l'ensemble pour lequel le rang de
, l'ensemble pour lequel le rang de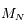 est
est 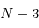 ,
, 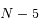 ,..., est de mesure nulle.
Ainsi étant donnée par exemple
,..., est de mesure nulle.
Ainsi étant donnée par exemple 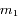 , il y aura une et une seule solution
, il y aura une et une seule solution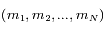 pour laquelle
pour laquelle 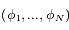 est une configuration d'équilibre.
est une configuration d'équilibre.