SOLUTION

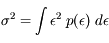
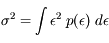
L'erreur quadratique moyenne se calcule de façon classique : $\sigma^2 = \int{\epsilon^2\;p(\epsilon)\;d\epsilon}$

Après correction du biais, la densité de probabilité de l'erreur est uniforme dans l'intervalle [-q/2, q/2] :

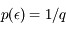$p(\epsilon) = 1/q$ dans l'intervalle [-q/2, q/2]

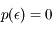$p(\epsilon) = 0$ ailleurs

Erreur de numérisation

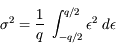
$\sigma^2 = \frac{1}{q}\;\int_{-q/2}^{q/2}{\epsilon^2\;d\epsilon}$

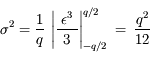
$\sigma^2 = \frac{1}{q}\; \left|\frac{\;\epsilon^3\;}{3} \right|_{-q/2}^{q/2} \: = \:\frac{q^2}{12}$

Soit un écart-type 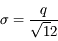$\sigma = \frac{q}{\sqrt 12}$ ou encore 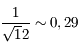$\frac{1}{\sqrt 12} \sim 0,29$ bits.

(on remarque que le coefficient 1/12 provient de l'intégration, et n'a rien à voir avec le nombre de bits utilisés)