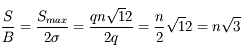Auteur: Jérôme Thiébaut
Les supernovae de type 1A correspondent à l'explosion d'une étoile de type naine blanche suite à l'accrétion de matière arrachée à une étoile géante proche. Ces phénomènes extrêmement lumineux sont visibles de très loin ce qui permet leurs détections. La courbe de luminosité d'une SN1A est caractéristique et permet de déterminer sa magnitude absolue. Le but de cet exercice est de montrer comment grâce à des mesures de luminosité, on peut déterminer le redshift de l'étoile, et donc de la galaxie hôte. Le redshift étant une mesure de la distance, les SN1A servent de balises pour mesurer les distances dans l'univers.
Courbe de lumière d'une supernova.
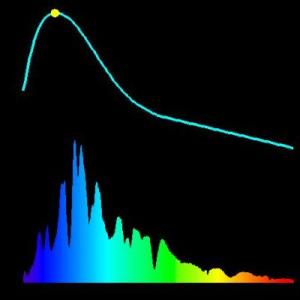
Courbe de lumière et spectre au maximum d'intensité d'une supernova.
Crédit :
Supernova Cosmology Project, Berkeley University
Auteur: Jérôme Thiébaut
 Supernova 1A
Supernova 1A
Difficulté : ☆
Temps : 30 min
On observe une supernova de type 1A dans une galaxie et on mesure sa magnitude apparente 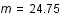 . Grâce à sa courbe de lumière, on détermine sa magnitude absolue
. Grâce à sa courbe de lumière, on détermine sa magnitude absolue 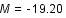 .
.
Question 1)
On exprime la distance luminosité, 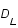 , comme suit:
, comme suit:
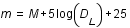 , où
, où 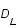 est exprimée en mégaparsec (Mpc) (Le parsec étant une unité de distance correspondant à
est exprimée en mégaparsec (Mpc) (Le parsec étant une unité de distance correspondant à 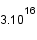 m).
m).
Calculer sa valeur.
Question 3)
Calculer r, puis sachant que la distance luminosité et la distance r sont reliées par la relation 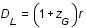 (dans le modèle cosmologique standart
(dans le modèle cosmologique standart 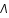 CDM), déterminer l'équation du second degré à laquelle obéit
CDM), déterminer l'équation du second degré à laquelle obéit 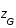 .
.
Question 4)
Résoudre cette équation et déterminer la valeur du redshift 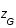 (positive par définition).
On donne
(positive par définition).
On donne  et
et 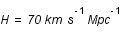 .
.
Auteur: Stéphane Erard
Les instruments modernes utilisent des détecteurs numériques tels que des CCD, c'est-à-dire qu'ils fournissent en sortie un signal numérisé sur un nombre fini de valeurs. Cette étape produit une erreur d'arrondi appelée "bruit de quantification" ou "bruit de numérisation" qui peut dans certains cas limiter la précision de la mesure. On étudie ici la statistique de ce bruit.
Auteur: Stéphane Erard
 Bruit de numérisation
Bruit de numérisation
Difficulté : ☆
Temps : 30 min
L'exercice consiste à estimer l'erreur due à la numérisation (ou quantification) d'un signal continu.
Question 1)
On mesure un signal lumineux avec une caméra CCD. Tracer l'allure de la fonction de réponse du convertisseur analogique/numérique (CAN). Si le convertisseur fonctionne sur 12 bits, combien de valeurs sont disponibles en sortie ?
Le convertisseur est réglé pour couvrir la dynamique de la caméra jusqu'à un niveau analogique 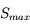 . Quel est le pas de numérisation du signal ?
. Quel est le pas de numérisation du signal ?
Question 2)
Estimer l'erreur quadratique moyenne due à la numérisation.
L'erreur est la différence entre le signal d'entrée et le signal de sortie, similaire à une erreur d'arrondi :
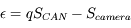
On commence par corriger de l'erreur systématique (biais, ou offset) en centrant la différence — ce biais est de 1/2 pas-codeur :
Offset
Question 3)
Calculer le rapport signal sur bruit correspondant. Comment peut-on améliorer celui-ci, et jusqu'à quel point ?
Question 4)
Comparer aux autres sources de bruit.
-
Question 1
Solution :
Le signal d'entrée, continu, est mesuré par le CCD puis numérisé par le CAN. La sortie est donc discrète, codée sur 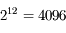 niveaux. Ces niveaux sont appelés ADU (Analog-to-Digital Units), DN (Digital Numbers) ou pas-codeurs en français.
niveaux. Ces niveaux sont appelés ADU (Analog-to-Digital Units), DN (Digital Numbers) ou pas-codeurs en français.
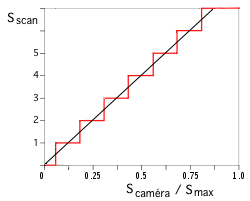
La courbe de réponse donne la sortie du système de mesure en fonction de son entrée :
Numérisation
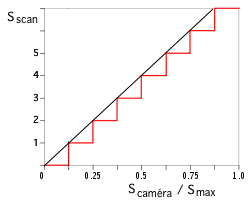
Sur n bits, le pas de numérisation du signal de sortie est q = 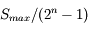
-
Question 2
Aide :
L'erreur est la différence entre le signal d'entrée et le signal de sortie, similaire à une erreur d'arrondi :
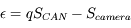
On commence par corriger de l'erreur systématique (biais, ou offset) en centrant la différence — ce biais est de 1/2 pas-codeur :
Offset

Solution :
L'erreur quadratique moyenne se calcule de façon classique :
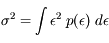
Après correction du biais, la densité de probabilité de l'erreur est uniforme dans l'intervalle [-q/2, q/2] :
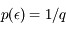 dans l'intervalle [-q/2, q/2]
dans l'intervalle [-q/2, q/2]
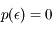 ailleurs
ailleurs
Erreur de numérisation
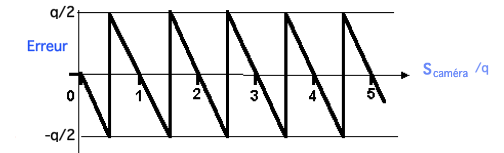
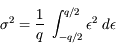
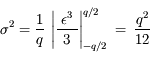
Soit un écart-type 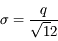 ou encore
ou encore 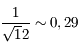 bits.
bits.
(on remarque que le coefficient 1/12 provient de l'intégration, et n'a rien à voir avec le nombre de bits utilisés)
-
Question 3
Solution :
Le signal maximum est 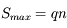 . En rapportant au signal moyen, on trouve :
. En rapportant au signal moyen, on trouve :
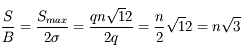
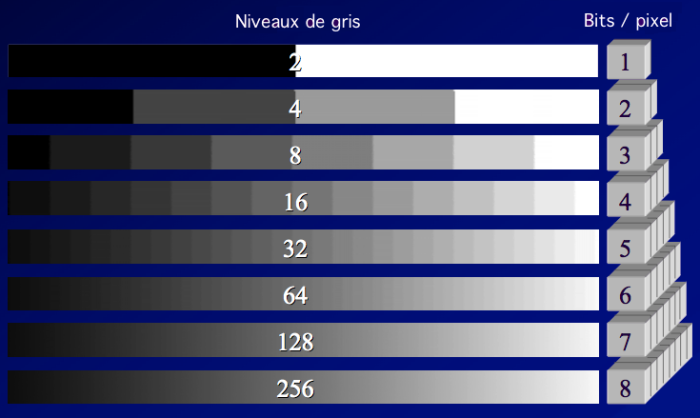
La seule façon de réduire le bruit de numérisation est de coder le signal sur un plus grand nombre de bits n. La différence de "grain" est très perceptible à l'œil nu avec une échelle de gris codée sur un nombre variable de bits. A partir de 256 niveaux, la variation apparaît quasiment continue, ce qui veut dire que le pas de quantification devient petit devant l'incertitude de lecture de l'œil. De la même façon, les CD audio sont codés sur 16 bits pour éliminer le bruit de numérisation ; celui-ci est encore très audible avec un codage sur 8 bits.
Résolution numérique
-
Question 4
Solution :
On ajuste habituellement le pas de numérisation pour coder le bruit physique sur 1 pas-codeur : un pas plus petit n'apporterait pas d'information supplémentaire sur le signal. En général, c'est le bruit de lecture qui domine le bruit intrinsèque de la source (bruit de photon). Le bruit de numérisation est alors bien plus petit. Si la chaîne de détection est bien réglée, celui-ci ne limite donc jamais la mesure.

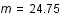 . Grâce à sa courbe de lumière, on détermine sa magnitude absolue
. Grâce à sa courbe de lumière, on détermine sa magnitude absolue 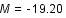 .
.
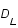 , comme suit:
, comme suit:
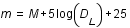 , où
, où 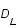 est exprimée en mégaparsec (Mpc) (Le parsec étant une unité de distance correspondant à
est exprimée en mégaparsec (Mpc) (Le parsec étant une unité de distance correspondant à 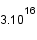 m).
m).
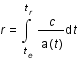 , où c est la vitesse de la lumière, t le temps,
, où c est la vitesse de la lumière, t le temps, 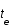 le temps d'émission de la lumière par la galaxie,
le temps d'émission de la lumière par la galaxie, 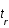 celui de réception par l'observateur et a(t) le facteur d'échelle décrivant l'expansion de l'univers.
celui de réception par l'observateur et a(t) le facteur d'échelle décrivant l'expansion de l'univers.
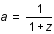 et que par définition
et que par définition 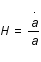 ; exprimer la distance r sous forme d'une intégrale selon z (on posera qu'à
; exprimer la distance r sous forme d'une intégrale selon z (on posera qu'à 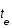 ,
, 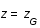 et par définition à
et par définition à 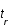 , z=0).
, z=0).
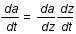 exprimer
exprimer 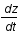 en fonction de z et H.
en fonction de z et H.
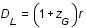 (dans le modèle cosmologique standart
(dans le modèle cosmologique standart 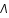 CDM), déterminer l'équation du second degré à laquelle obéit
CDM), déterminer l'équation du second degré à laquelle obéit 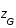 .
.
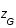 (positive par définition).
On donne
(positive par définition).
On donne  et
et 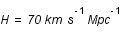 .
.
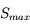 . Quel est le pas de numérisation du signal ?
. Quel est le pas de numérisation du signal ?
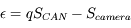

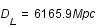
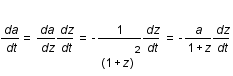
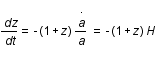
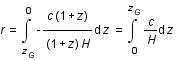
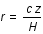 donc
donc 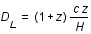 .
.
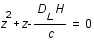 .
.
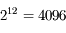 niveaux. Ces niveaux sont appelés ADU (Analog-to-Digital Units), DN (Digital Numbers) ou
niveaux. Ces niveaux sont appelés ADU (Analog-to-Digital Units), DN (Digital Numbers) ou 
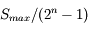
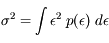
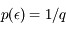 dans l'intervalle [-q/2, q/2]
dans l'intervalle [-q/2, q/2]
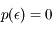 ailleurs
ailleurs

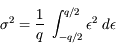
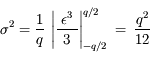
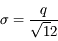 ou encore
ou encore 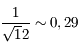 bits.
bits.
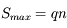 . En rapportant au signal moyen, on trouve :
. En rapportant au signal moyen, on trouve :