Un méridien étant un demi-grand cercle passant par les pôles du cercle de référence, comme les deux méridiens en question sont opposés l'un à l'autre par rapport à l'axe des pôles (ici l'axe zénith-nadir), ils forment à eux deux un grand cercle de 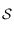 . Comme c'est un grand cercle son rayon est
. Comme c'est un grand cercle son rayon est 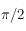 (en tant que cercle de
(en tant que cercle de 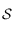 ). Son centre, sur la sphère, se trouve donc sur l'axe des pôles du grand cercle. Cette axe est perpendiculaire au plan contenant le grand cercle et il passe par le centre de la sphère, il est donc compris dans le plan de l'horizon céleste et est perpendiculaire à la droite d'intersection entre le grand cercle défini par les méridiens et l'horizon céleste. On en déduit que son azimut est égal à
). Son centre, sur la sphère, se trouve donc sur l'axe des pôles du grand cercle. Cette axe est perpendiculaire au plan contenant le grand cercle et il passe par le centre de la sphère, il est donc compris dans le plan de l'horizon céleste et est perpendiculaire à la droite d'intersection entre le grand cercle défini par les méridiens et l'horizon céleste. On en déduit que son azimut est égal à 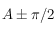 (deux solutions possibles).
(deux solutions possibles).
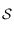 . Comme c'est un grand cercle son rayon est
. Comme c'est un grand cercle son rayon est 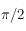 (en tant que cercle de
(en tant que cercle de 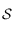 ). Son centre, sur la sphère, se trouve donc sur l'axe des pôles du grand cercle. Cette axe est perpendiculaire au plan contenant le grand cercle et il passe par le centre de la sphère, il est donc compris dans le plan de l'horizon céleste et est perpendiculaire à la droite d'intersection entre le grand cercle défini par les méridiens et l'horizon céleste. On en déduit que son azimut est égal à
). Son centre, sur la sphère, se trouve donc sur l'axe des pôles du grand cercle. Cette axe est perpendiculaire au plan contenant le grand cercle et il passe par le centre de la sphère, il est donc compris dans le plan de l'horizon céleste et est perpendiculaire à la droite d'intersection entre le grand cercle défini par les méridiens et l'horizon céleste. On en déduit que son azimut est égal à 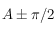 (deux solutions possibles).
(deux solutions possibles).