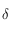 n'est pas définie si
n'est pas définie si 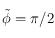 . On rappelle que
. On rappelle que 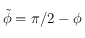 , comme
, comme ![\phi\in[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation359.png) ,
c'est bien la seule valeur interdite pour
,
c'est bien la seule valeur interdite pour 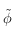 . Cette valeur correspond donc à
. Cette valeur correspond donc à 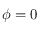 , c'est-à-dire à un point de l'équateur terrestre.
, c'est-à-dire à un point de l'équateur terrestre.
Avant tout, on remarque que la fonction 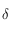 n'est pas définie si
n'est pas définie si 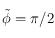 . On rappelle que
. On rappelle que 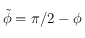 , comme
, comme ![\phi\in[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation359.png) ,
c'est bien la seule valeur interdite pour
,
c'est bien la seule valeur interdite pour 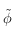 . Cette valeur correspond donc à
. Cette valeur correspond donc à 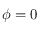 , c'est-à-dire à un point de l'équateur terrestre.
, c'est-à-dire à un point de l'équateur terrestre.
Pour tout autre latitude, 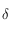 est définie, continue et dérivable sur
est définie, continue et dérivable sur 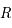 . On remarque que
. On remarque que 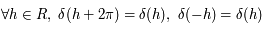 donc la fonction
donc la fonction 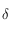 est
est 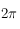 périodique et paire. En outre on a aussi
périodique et paire. En outre on a aussi 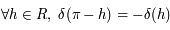 , ainsi le point de coordonnée
, ainsi le point de coordonnée 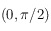 est un centre de symétrie pour la courbe représentative de
est un centre de symétrie pour la courbe représentative de 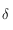 .
.
Il suffit donc d'étudier 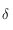 pour
pour ![h\in[0,\pi/2]](../pages_trigo/equations_trigo/equation371.png) .
.
On a : 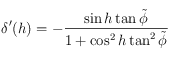 , ainsi le tableau de variation de
, ainsi le tableau de variation de 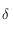 sur
sur ![[0,\pi/2]](../pages_trigo/equations_trigo/equation374.png) est:
est:
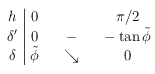
Ceci permet de tracer la courbe représentative de 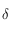 entre
entre ![[0,\pi/2]](../pages_trigo/equations_trigo/equation377.png) , puis on complète par symétrie centrale par rapport au point de coordonnées
, puis on complète par symétrie centrale par rapport au point de coordonnées 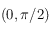 , puis par symétrie axiale par rapport à l'axe des ordonnées, ce qui permet de tracer la courbe entre
, puis par symétrie axiale par rapport à l'axe des ordonnées, ce qui permet de tracer la courbe entre ![[-\pi,0]](../pages_trigo/equations_trigo/equation379.png) . On obtient alors la courbe entre
. On obtient alors la courbe entre ![[0,2\pi]](../pages_trigo/equations_trigo/equation380.png) en utilisant la périodicité de
en utilisant la périodicité de 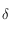 .
.