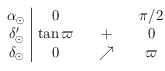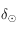 est définie continue dérivable sur
est définie continue dérivable sur 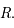 On a
On a 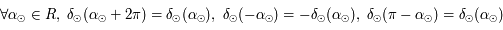 . Ainsi
. Ainsi 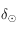 est
est 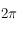 périodique, elle est impaire, et sa courbe représentative est symétrique par rapport à l'axe
périodique, elle est impaire, et sa courbe représentative est symétrique par rapport à l'axe 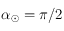 .
.
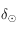 est définie continue dérivable sur
est définie continue dérivable sur 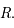 On a
On a 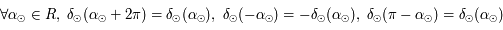 . Ainsi
. Ainsi 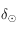 est
est 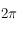 périodique, elle est impaire, et sa courbe représentative est symétrique par rapport à l'axe
périodique, elle est impaire, et sa courbe représentative est symétrique par rapport à l'axe 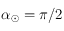 .
.
Ainsi, il suffit d'étudier 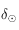 sur
sur ![[0,\pi/2]](../pages_trigo/equations_trigo/equation404.png) . On a
. On a 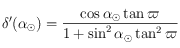 , ainsi le tableau de variation de
, ainsi le tableau de variation de 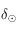 est :
est :