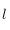SOLUTION

La date du jour permet de déterminer le nombre de jour écoulés depuis l'équinoxe de printemps (22 Mars environ). Ceci permet de connaître l'angle entre la direction du point vernal et le Soleil, mesuré sur l'écliptique. On note 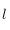cet angle.

On utilise le triangle sphérique défini par le point vernal, noté 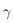$\gamma$ , le Soleil et le point d'intersection entre le méridien équatorial passant par le Soleil et l'équateur céleste. On a ainsi le triangle sphérique suivant :

triangle sphérique pour le Soleil

Crédit : Astrophysique sur Mesure / Marc Fouchard

En appliquant les formules à ce triangle on obtient:

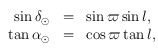
$\begin{array}{rcl}\sin \delta_\odot &=& \sin \varpi \sin l, \\ \tan \alpha_\odot &=& \cos \varpi \tan l, \end{array}$

où 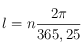$l=n\frac{2\pi}{365,25}$ avec 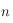égal au nombre de jours écoulés depuis le 22 mars (le nombre de jours dans une année étant égal à 365,25) et le symbole $\odot$ se réfère au Soleil.

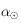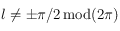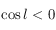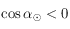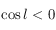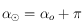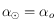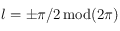Pour $\alpha_\odot$ , si $l\ne \pm \pi/2 \,\rm{mod}(2\pi)$ alors $\alpha_o=\arctan(\cos \varpi \tan l) \in ]-\pi/2,\pi/2[$ est solution de la deuxième équation, ainsi que $\alpha_o+\pi$ . Mais en remarquant que si $\cos l < 0$ alors $\cos \alpha_\odot < 0$ , on en déduit que si $\cos l < 0$ alors $\alpha_\odot = \alpha_o+\pi$ , sinon $\alpha_\odot=\alpha_o$ . 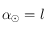Si $l=\pm \pi/2\,\rm{mod}(2\pi)$ alors $\alpha_\odot = l$ . On prendra bien soin ensuite de transformer 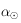$\alpha_\odot$ en un angle compris dans l'intervalle $[0,2\pi]$ .