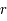 et
et 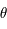 les coordonnées polaires de
les coordonnées polaires de 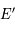 .
Le point
.
Le point 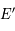 est dans demi-plan méridien passant par
est dans demi-plan méridien passant par 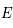 . Comme ce demi-plan permet de définir l'angle horaire
. Comme ce demi-plan permet de définir l'angle horaire 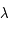 et que l'origine des angles horaires et des angles polaires dans
et que l'origine des angles horaires et des angles polaires dans 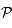 est la même, on a bien
est la même, on a bien 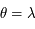 .
On se place alors dans le plan
.
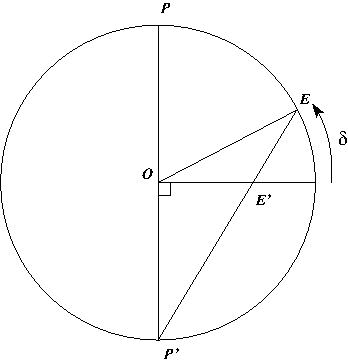
On se place alors dans le plan 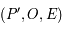 . Le triangle
. Le triangle 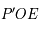 est isocèle en
est isocèle en 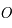 (voir la figure ci-dessous). Ainsi On en déduit que
(voir la figure ci-dessous). Ainsi On en déduit que 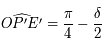 . Le triangle
. Le triangle 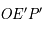 étant rectangle en
étant rectangle en 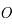 , on a donc:
, on a donc: 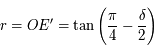 . On peut remarquer que cette formule est valable quelque soit
. On peut remarquer que cette formule est valable quelque soit ![\delta\in[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation59.png) .
.
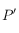 d'un point.
d'un point.