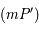et ét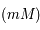ant deux tangentes à 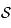, on a bien 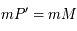(facilement démontré en utilisant le théorème de Pythagore aux triangles 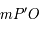et 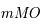). Les triangles 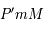et 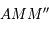sont en configuration de Thales. Comme 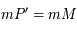on a bien 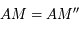. De même, les triangles 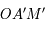et 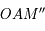forment une autre configuration de Thales, donc : 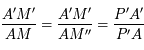. Ainsi 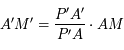. Ainsi la distance 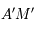est indépendante de la position du point 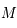sur 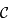, tout comme l'est la distance 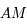. Donc le point 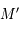se trouve sur un cercle de centre 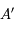. On voit que tout le cercle est obtenu lorsque 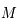décrit .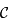