Le point 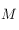 se trouvant sur l'horizon céleste, on a
se trouvant sur l'horizon céleste, on a 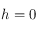 . La déclinaison étant dans l'intervalle
. La déclinaison étant dans l'intervalle ![[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation233.png) , elle est complètement déterminée par son sinus. Ainsi en utilisant la 4ème relation des équations données dans le préambule, on obtient:
, elle est complètement déterminée par son sinus. Ainsi en utilisant la 4ème relation des équations données dans le préambule, on obtient: 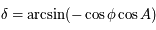 , où la fonction
, où la fonction 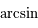 est la réciproque de la fonction sinus. Comme cette fonction est à valeur dans
est la réciproque de la fonction sinus. Comme cette fonction est à valeur dans ![[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation236.png) ,
, 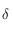 est complètement déterminé par cette relation.
est complètement déterminé par cette relation.

Connaissant 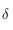 , la 5ème relation des équations données dans le préambule, nous permet d'avoir
, la 5ème relation des équations données dans le préambule, nous permet d'avoir 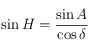 . Cette relation n'est pas définie pour les pôles (
. Cette relation n'est pas définie pour les pôles (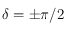 ), mais dans ce cas l'angle horaire
), mais dans ce cas l'angle horaire 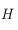 n'est pas définie non plus. D'autre part, on sait que la projection du pôle céleste nord est le centre de la sphère
n'est pas définie non plus. D'autre part, on sait que la projection du pôle céleste nord est le centre de la sphère 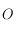 , alors que le pôle céleste sud est le seul point de la sphère céleste pour lequel la projection n'est pas définie.
, alors que le pôle céleste sud est le seul point de la sphère céleste pour lequel la projection n'est pas définie.
Soit 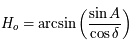 . On sait que
. On sait que ![H_o\in[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation246.png) , alors que
, alors que 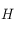 est dans l'intervalle
est dans l'intervalle ![[0, 2\pi]](../pages_trigo/equations_trigo/equation248.png) . Mais on sait que
. Mais on sait que 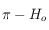 est aussi solution de l'équation pour
est aussi solution de l'équation pour 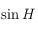 . Pour choisir quelle est la bonne solution, on doit utiliser la 6ème relation des équations données dans le préambule, qui nous permet d'avoir
. Pour choisir quelle est la bonne solution, on doit utiliser la 6ème relation des équations données dans le préambule, qui nous permet d'avoir 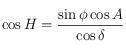 . Mais seul le signe de cette quantité nous intéresse puisque
. Mais seul le signe de cette quantité nous intéresse puisque 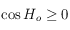 , alors que
, alors que 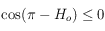 . Or comme
. Or comme ![\delta\in]-\pi/2,\pi/2[](../pages_trigo/equations_trigo/equation254.png) (les pôles sont exclus),
(les pôles sont exclus), 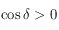 . Ainsi si
. Ainsi si 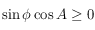 , on prend
, on prend 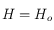 si
si 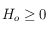 et
et 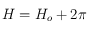 (qui est toujours solution, par périodicité, des deux équations que
(qui est toujours solution, par périodicité, des deux équations que 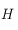 doit vérifier) si
doit vérifier) si 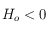 . Et si
. Et si 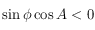 , on prend
, on prend 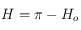 si
si 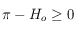 et
et 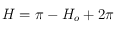 si
si 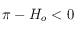 .
.
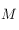 se trouvant sur l'horizon céleste, on a
se trouvant sur l'horizon céleste, on a 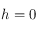 . La déclinaison étant dans l'intervalle
. La déclinaison étant dans l'intervalle ![[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation233.png) , elle est complètement déterminée par son sinus. Ainsi en utilisant la 4ème relation des équations données dans le préambule, on obtient:
, elle est complètement déterminée par son sinus. Ainsi en utilisant la 4ème relation des équations données dans le préambule, on obtient: 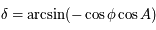 , où la fonction
, où la fonction 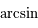 est la réciproque de la fonction sinus. Comme cette fonction est à valeur dans
est la réciproque de la fonction sinus. Comme cette fonction est à valeur dans ![[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation236.png) ,
, 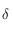 est complètement déterminé par cette relation.
est complètement déterminé par cette relation.

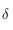 , la 5ème relation des équations données dans le
, la 5ème relation des équations données dans le 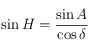 . Cette relation n'est pas définie pour les pôles (
. Cette relation n'est pas définie pour les pôles (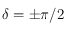 ), mais dans ce cas l'angle horaire
), mais dans ce cas l'angle horaire 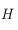 n'est pas définie non plus. D'autre part, on sait que la projection du pôle céleste nord est le centre de la sphère
n'est pas définie non plus. D'autre part, on sait que la projection du pôle céleste nord est le centre de la sphère 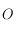 , alors que le pôle céleste sud est le seul point de la sphère céleste pour lequel la projection n'est pas définie.
, alors que le pôle céleste sud est le seul point de la sphère céleste pour lequel la projection n'est pas définie.
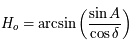 . On sait que
. On sait que ![H_o\in[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation246.png) , alors que
, alors que 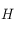 est dans l'intervalle
est dans l'intervalle ![[0, 2\pi]](../pages_trigo/equations_trigo/equation248.png) . Mais on sait que
. Mais on sait que 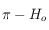 est aussi solution de l'équation pour
est aussi solution de l'équation pour 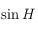 . Pour choisir quelle est la bonne solution, on doit utiliser la 6ème relation des équations données dans le
. Pour choisir quelle est la bonne solution, on doit utiliser la 6ème relation des équations données dans le 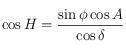 . Mais seul le signe de cette quantité nous intéresse puisque
. Mais seul le signe de cette quantité nous intéresse puisque 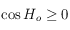 , alors que
, alors que 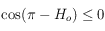 . Or comme
. Or comme ![\delta\in]-\pi/2,\pi/2[](../pages_trigo/equations_trigo/equation254.png) (les pôles sont exclus),
(les pôles sont exclus), 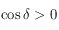 . Ainsi si
. Ainsi si 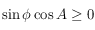 , on prend
, on prend 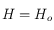 si
si 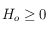 et
et 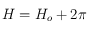 (qui est toujours solution, par périodicité, des deux équations que
(qui est toujours solution, par périodicité, des deux équations que 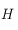 doit vérifier) si
doit vérifier) si 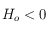 . Et si
. Et si 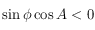 , on prend
, on prend 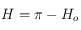 si
si 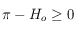 et
et 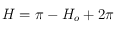 si
si 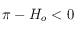 .
.