Auteur: Marc Fouchard
astrolabe

Astrolabe du XVI siècle.
Crédit :
David Monniaux, licence : CC BY-SA 3.0
L'astrolabe est un outil astronomique permettant de représenter la partie du ciel observée en fonction de la date et de l'heure pour un lieu donné. Il permet ensuite de faire différentes mesures comme la détermination des heures de lever et de coucher d'un astre. Les applications de l'astrolabe sont pourtant très nombreuses. Pour avoir plus de détails, on pourra aller voir l'astrolabe.
La construction d'un astrolabe repose sur la projection stéréographique. Le but de cet exercice est d'étudier les propriétés principales de cette projection et d'en déduire l'image de points et de cercles caractéristiques de la sphère céleste.
Ce sont ces constructions qui ont permis de construire l'animation suivante.
astrolabe 
 sphère céleste
sphère céleste
Sur une sphère céleste un point est repéré par une longitude et une latitude. La latitude correspond à un angle entre ![[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation1.png) donnant la hauteur au dessus d'un grand cercle de référence et en choisissant un côté positif (comme sur Terre, la latitude d'un lieu correspond à une hauteur au-dessus de l'équateur, comptée positivement dans l'hémisphère nord). Ce cercle de référence permet de définir l'axe des pôles et les pôles. La longitude correspond à l'angle, compris dans l'intervalle
donnant la hauteur au dessus d'un grand cercle de référence et en choisissant un côté positif (comme sur Terre, la latitude d'un lieu correspond à une hauteur au-dessus de l'équateur, comptée positivement dans l'hémisphère nord). Ce cercle de référence permet de définir l'axe des pôles et les pôles. La longitude correspond à l'angle, compris dans l'intervalle ![[0,2\pi]](../pages_trigo/equations_trigo/equation2.png) , entre un méridien de référence et le méridien passant par le point considéré. Cet angle est mesuré sur le cercle de référence en choisissant un sens positif.
Sur la Terre les longitudes sont mesurées à partir du méridien passant par Greenwich en prenant comme sens positif la direction de l'Ouest (ce qui correspond au sens des aiguilles d'une montre lorsqu'on regarde du pôle nord).
, entre un méridien de référence et le méridien passant par le point considéré. Cet angle est mesuré sur le cercle de référence en choisissant un sens positif.
Sur la Terre les longitudes sont mesurées à partir du méridien passant par Greenwich en prenant comme sens positif la direction de l'Ouest (ce qui correspond au sens des aiguilles d'une montre lorsqu'on regarde du pôle nord).
Dans notre cas, la sphère céleste 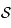 est une sphère de rayon unité (arbitraire), centrée sur l'observateur. Sur cette sphère on projette l'équateur terrestre, ce qui nous donne un grand cercle , appelé équateur céleste, le pôle nord se projette au point
est une sphère de rayon unité (arbitraire), centrée sur l'observateur. Sur cette sphère on projette l'équateur terrestre, ce qui nous donne un grand cercle , appelé équateur céleste, le pôle nord se projette au point 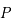 et le pôle sud au point
et le pôle sud au point 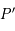 , appelés respectivement pôle céleste nord et pôle céleste sud.
, appelés respectivement pôle céleste nord et pôle céleste sud.
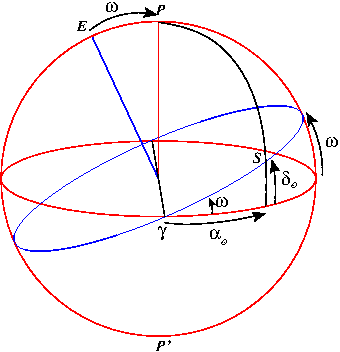
En astronomie différents ensembles de longitude et de latitude sont utilisés :
- les coordonnées locales : le grand cercle de référence correspond à la projection de l'horizon sur la sphère céleste. Les pôles sont donc la direction de la verticale du lieu appelé zénith et la direction opposée appelée Nadir. Ainsi, la latitude correspond à une hauteur sur l'horizon céleste, notée
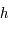 et positive au dessus de l'horizon, et une longitude mesurée sur l'horizon céleste, appelée azimut et notée
et positive au dessus de l'horizon, et une longitude mesurée sur l'horizon céleste, appelée azimut et notée 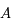 , en prenant comme méridien d'origine celui passant par le pôle céleste sud et comme sens positif vers l'ouest.
, en prenant comme méridien d'origine celui passant par le pôle céleste sud et comme sens positif vers l'ouest.
- Les coordonnées horaires : définies par rapport à l'équateur céleste, avec une latitude, appelée déclinaison et notée
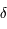 , positive vers le pôle céleste nord, et une longitude appelée angle horaire et noté
, positive vers le pôle céleste nord, et une longitude appelée angle horaire et noté 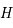 , avec comme méridien d'origine le méridien passant par le zénith et comme sens positif vers l'ouest.
, avec comme méridien d'origine le méridien passant par le zénith et comme sens positif vers l'ouest.
- Les coordonnées équatoriales :même latitude que le précédent mais la longitude, appelée ascension droite et notée
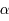 , est mesurée par rapport au méridien d'origine qui contient la position du Soleil au moment de l'équinoxe de printemps et le sens positif est le sens trigonométrique (vue du pôle nord). Cette position est appelé le point vernal et ce sens positif correspond au sens du mouvement annuel du Soleil.
, est mesurée par rapport au méridien d'origine qui contient la position du Soleil au moment de l'équinoxe de printemps et le sens positif est le sens trigonométrique (vue du pôle nord). Cette position est appelé le point vernal et ce sens positif correspond au sens du mouvement annuel du Soleil.
La figure ci-dessous montre la correspondance entre ces différents systèmes de coordonnées. On remarquera aussi sur la figure le lien entre la position du zénith et la latitude terrestre du lieu.
sphère céleste
Les coordonnées utilisées en astronomie. Le
grand cercle vert correspond à l'horizon céleste et le rouge à l'équateur céleste. La hauteur du pôle céleste nord sur l'horizon correspond à la latitude du lieu. Le point
correspond à la direction du
point vernal.
En un lieu de latitude 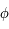 on a alors les équations suivantes permettant de passer d'un ensemble de coordonnées à l'autre:
on a alors les équations suivantes permettant de passer d'un ensemble de coordonnées à l'autre:
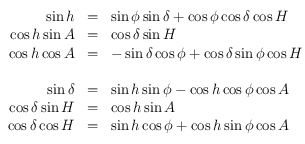
Le lien entre l'ascension droite et l'angle horaire se fait en utilisant l'angle horaire du point vernal appelé temps sidéral, que l'on notera 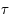 . On a la relation :
. On a la relation : 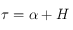 .
.
Auteur: Marc Fouchard
 Astrolabe
Astrolabe
Difficulté : ☆☆
Temps : 2h
Question 3)
Montrer que la projection d'un cercle 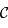 passant par le pôle céleste Sud
passant par le pôle céleste Sud  est une droite.
est une droite.
Question 10)
La trajectoire apparente du Soleil vue depuis la Terre est dans un plan appelé écliptique. L'inclinaison entre le plan de l'écliptique et le plan de l'équateur est constante et est appelée obliquité, notée 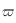 . Les variations de l'obliquité sont tellement faibles qu'on peut la supposer constante ici. La droite d'intersection entre ces deux plans passe par le point vernal et le centre de la sphère céleste
. Les variations de l'obliquité sont tellement faibles qu'on peut la supposer constante ici. La droite d'intersection entre ces deux plans passe par le point vernal et le centre de la sphère céleste 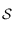 .
En s'aidant d'un dessin, déterminer les coordonnées équatoriales, puis les coordonnées horaires du pôle de l'écliptique
.
En s'aidant d'un dessin, déterminer les coordonnées équatoriales, puis les coordonnées horaires du pôle de l'écliptique 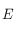 ayant une déclinaison positive.
ayant une déclinaison positive.
Question 11)
En déduire la méthode pour construire la projection de l'écliptique.
Auteur: Marc Fouchard
Le but de cet exercice est de construire une carte illustrant la partie visible du ciel en un lieu donné en fonction de la date et de l'heure.
On peut voir dans l'animation ci-dessous le résultat final de cet exercice. L'horizon est fixe tandis que le fond d'étoiles fixes et le Soleil défilent à cause de la rotation de la Terre sur elle-même.
carte du ciel 
Pour bien comprendre le but de l'exercice, il faut bien assimiler les deux sphères célestes qui interviennent ici.
On pourra aller voir cette page où ces deux sphères sont présentées, ainsi que les 3 principaux systèmes de coordonnées utilisés en astronomie.
Auteur: Marc Fouchard
 Carte du ciel
Carte du ciel
Difficulté : ☆
Temps : 2h
Question 1)
L'exercice se fait en deux étapes, la première consiste à construire le profile de l'horizon, et la deuxième à placer sur cet horizon le fond d'étoiles fixes contenant la trajectoire apparente annuelle du Soleil.
On se place en un lieu de latitude 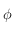 . Dessiner sur une sphère céleste avec l'équateur céleste comme plan de référence, le pôle céleste nord, l'horizon céleste, et les points cardinaux Sud, Ouest, Nord et Est. On notera aussi
. Dessiner sur une sphère céleste avec l'équateur céleste comme plan de référence, le pôle céleste nord, l'horizon céleste, et les points cardinaux Sud, Ouest, Nord et Est. On notera aussi 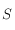 le point d'intersection du méridien passant par les pôles célestes nord et sud et par le zénith avec l'équateur céleste. On notera
le point d'intersection du méridien passant par les pôles célestes nord et sud et par le zénith avec l'équateur céleste. On notera 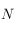 le point opposé à
le point opposé à 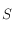 sur l'équateur céleste.
sur l'équateur céleste.

On mettra en évidence les angles suivants sur la figure: la déclinaison 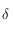 d'un point
d'un point 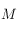 de l'horizon céleste, la latitude, la colatitude
de l'horizon céleste, la latitude, la colatitude 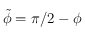 , et l'angle
, et l'angle 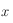 entre la direction ouest et le méridien équatorial passant par
entre la direction ouest et le méridien équatorial passant par  ,et compté positivement vers
,et compté positivement vers 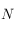 .
.
Question 2)
En utilisant la formule suivante, valable dans un triangle sphérique (voir le dessin ci-dessous),
déterminer la déclinaison 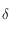 de
de 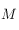 en fonction de
en fonction de 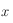 et
et 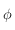 .
.
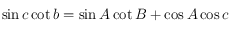 .
.
triangle sphérique
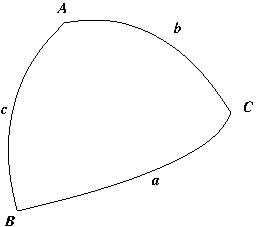
Triangle sphérique: les côtés correspondent à des arcs de
grands cercles. Comme la
sphère céleste est de rayon unité, la longueur d'un de ces arcs correspond à l'angle sous lequel est vu cet arc depuis le centre de la sphère.
Question 5)
On souhaite maintenant déterminer l'équation de la trajectoire apparente annuelle du Soleil (qui est dans un plan appelé éclitpique) dans un repère où on a l'ascension droite en abscisse et la déclinaison en ordonnées.
La normale au plan de l'écliptique dirigée vers l'hémisphère nord a une direction constante par rapport à la direction du pôle céleste nord 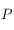 . L'angle entre ces deux directions est appelé obliquité est vaut
. L'angle entre ces deux directions est appelé obliquité est vaut 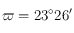 . Vu du pôle céleste nord, le Soleil décrit sa trajectoire dans le sens trigonométrique, c'est-à-dire que son ascension droite augmente au cours du temps.
. Vu du pôle céleste nord, le Soleil décrit sa trajectoire dans le sens trigonométrique, c'est-à-dire que son ascension droite augmente au cours du temps.
Faire un dessin de la sphère des fixes mettant en évidence l'équateur céleste, le grand cercle de l'écliptique et les coordonnées équatoriales du Soleil.
Question 6)
En déduire 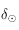 en fonction de
en fonction de 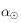 et de l'obliquité
et de l'obliquité 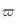 .
.
Question 8)
Déterminer les coordonnées du Soleil, aux équinoxes et aux solstices.
Question 9)
Il s'agit maintenant de positionner les deux graphes l'un par rapport à l'autre. C'est le Soleil qui fait le lien entre les deux.
Il faut d'abord placer le Soleil en fonction de la date du jours.
Une fois celui-ci positionné, il est facile de placer le graphe de l'horizon pour une heure solaire vraie donnée, puisque l'abscisse du Soleil sur cette carte correspond à l'heure solaire vraie. Ainsi lorsque le temps s'écoule le graphe de l'horizon va glisser sur le graphe des étoiles fixes et de l'écliptique (ou l'inverse suivant comment on choisi la transparence).
Il faut faire attention au fait que pour le graphe comportant l'horizon céleste, l'axe des abcisses est orienté de la droite vers la gauche, alors que pour la carte des étoiles fixes avec l'écliptique, l'axe des abscisses est orienté de la gauche vers la droite. Les deux axes vont de 0 à 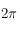 (en astronomie cependant on préfère noter les longitudes entre 0h et 24h).
(en astronomie cependant on préfère noter les longitudes entre 0h et 24h).
Déterminer l'ascension droite du Soleil en fonction de la date du jours (ceci permet finalement de résoudre complètement l'animation présentée dans l'introduction à cet exercice).
On utilisera la relation suivante valable dans un triangle sphérique de sommet 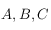 et de côté
et de côté 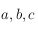 (
(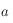 étant le côté opposé au sommet
étant le côté opposé au sommet 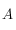 , etc.) où
, etc.) où  (voir la figure ci-dessous) :
(voir la figure ci-dessous) :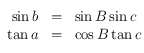 .
.
triangle sphérique

-
Question 1
Solution :
L'image du pôle 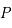 est le centre de la sphère
est le centre de la sphère 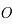 . L'ensemble des points invariants sont les points intersection de la sphère céleste
. L'ensemble des points invariants sont les points intersection de la sphère céleste 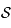 avec le plan
avec le plan 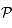 . C'est l'équateur céleste.
. C'est l'équateur céleste.
-
Question 2
Aide :
Faire un dessin dans le plan 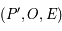 qui contient aussi le point
qui contient aussi le point 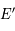 et le pôle céleste nord
et le pôle céleste nord 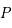 .
.
Solution :
Soit 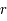 et
et 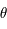 les coordonnées polaires de
les coordonnées polaires de 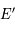 .
Le point
.
Le point 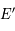 est dans demi-plan méridien passant par
est dans demi-plan méridien passant par 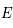 . Comme ce demi-plan permet de définir l'angle horaire
. Comme ce demi-plan permet de définir l'angle horaire 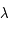 et que l'origine des angles horaires et des angles polaires dans
et que l'origine des angles horaires et des angles polaires dans 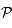 est la même, on a bien
est la même, on a bien 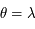 .
On se place alors dans le plan
.
On se place alors dans le plan 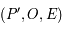 . Le triangle
. Le triangle 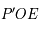 est isocèle en
est isocèle en 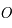 (voir la figure ci-dessous). Ainsi On en déduit que
(voir la figure ci-dessous). Ainsi On en déduit que 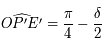 . Le triangle
. Le triangle 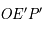 étant rectangle en
étant rectangle en 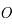 , on a donc:
, on a donc: 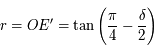 . On peut remarquer que cette formule est valable quelque soit
. On peut remarquer que cette formule est valable quelque soit ![\delta\in[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation59.png) .
.
projection d'un point
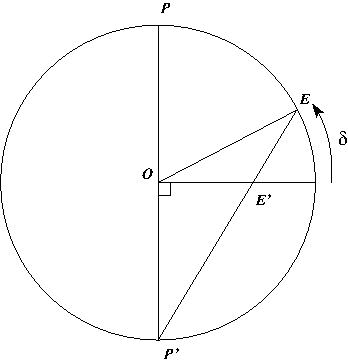
Projection stéréographique de pôle
d'un point.
-
Question 3
Solution :
Soit  le plan contenant le cercle
le plan contenant le cercle  Comme
Comme 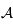 contient aussi
contient aussi 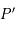 , on en déduit que les images des points de
, on en déduit que les images des points de 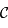 sont dans
sont dans  et par définition ils sont aussi dans
et par définition ils sont aussi dans 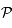 . L'intersection de deux plans étant une droite, on remarque que les images de
. L'intersection de deux plans étant une droite, on remarque que les images de 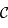 se trouvent bien sur une droite, notée
se trouvent bien sur une droite, notée 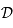 .
.
Soit 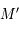 un point de
un point de 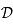 . La droite
. La droite 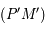 coupe le cercle
coupe le cercle 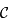 en un point
en un point 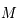 autre que
autre que 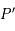 puisqu'elle n'est pas tangente à
puisqu'elle n'est pas tangente à 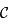 . Ainsi,
. Ainsi, 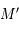 est l'image de
est l'image de 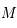 par la projection. Donc l'image de
par la projection. Donc l'image de 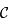 est la droite
est la droite 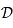 toute entière.
toute entière.
-
Question 4
Solution :
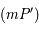 et
et 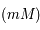 étant deux tangentes à
étant deux tangentes à 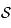 , on a bien
, on a bien 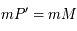 (facilement démontré en utilisant le théorème de Pythagore aux triangles
(facilement démontré en utilisant le théorème de Pythagore aux triangles 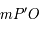 et
et 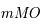 ). Les triangles
). Les triangles 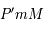 et
et 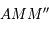 sont en configuration de Thales. Comme
sont en configuration de Thales. Comme 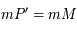 on a bien
on a bien 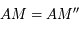 . De même, les triangles
. De même, les triangles 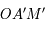 et
et 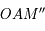 forment une autre configuration de Thales, donc :
forment une autre configuration de Thales, donc : 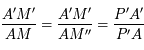 . Ainsi
. Ainsi 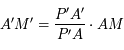 . Ainsi la distance
. Ainsi la distance 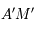 est indépendante de la position du point
est indépendante de la position du point 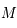 sur
sur 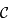 , tout comme l'est la distance
, tout comme l'est la distance 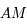 .
Donc le point
.
Donc le point 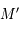 se trouve sur un cercle de centre
se trouve sur un cercle de centre 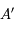 . On voit que tout le cercle est obtenu lorsque
. On voit que tout le cercle est obtenu lorsque 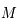 décrit
décrit 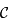 .
.
-
Question 5
Solution :
Les triangles 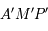 et
et 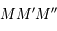 sont en configuration de Thales. On a donc:
sont en configuration de Thales. On a donc:
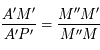 . Puis, avec la configuration de Thales des triangles
. Puis, avec la configuration de Thales des triangles 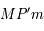 et
et 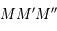 on a
on a 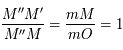 .
De nouveau on a bien l'image de
.
De nouveau on a bien l'image de 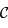 qui est un cercle de centre
qui est un cercle de centre 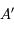 .
.
-
Question 6
Solution :
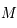 et
et 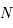 sont sur le même méridien que
sont sur le même méridien que 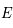 (ou sur le méridien opposé). Ainsi,
la latitude est obtenue à partir de celle de
(ou sur le méridien opposé). Ainsi,
la latitude est obtenue à partir de celle de 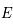 en ajoutant où en retranchant
en ajoutant où en retranchant 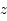 . Mais la latitude finale doit toujours être comprise dans l'intervalle
. Mais la latitude finale doit toujours être comprise dans l'intervalle ![[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation177.png) . Si elle est en dehors de cet intervalle alors, il faut prendre la latitude opposée et lui ajouter
. Si elle est en dehors de cet intervalle alors, il faut prendre la latitude opposée et lui ajouter 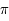 , et aussi prendre l'opposé de la longitude.
, et aussi prendre l'opposé de la longitude.
coordonnées M et N
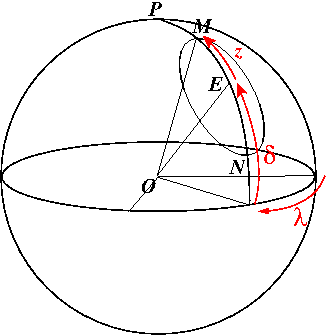
Positions des points
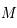
et
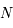
.
Ainsi, si 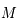 est obtenue en ajoutant
est obtenue en ajoutant 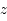 et
et 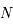 en retranchant
en retranchant 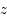 à
à 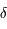 on a :
on a :
pour 
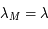 et
et 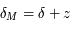 si
si 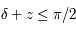 et
et
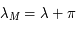 et
et 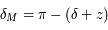 si
si 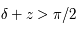 ,
,
et pour 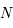 :
: 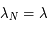 et
et 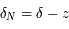 si
si 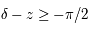 et
et
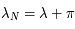 et
et 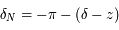 si
si 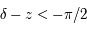 .
.
-
Question 7
Solution :
Le point 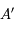 des constructions précédentes , et centre de la projection du cercle, se trouve dans le plan
des constructions précédentes , et centre de la projection du cercle, se trouve dans le plan 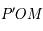 et dans le plan
et dans le plan 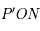 . Or ces deux plans sont confondus. Donc, les points
. Or ces deux plans sont confondus. Donc, les points 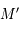 ,
, 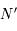 et
et 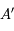 sont sur la droite intersection des plans
sont sur la droite intersection des plans 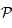 et
et 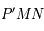 . Ils sont donc alignés.
. Ils sont donc alignés. 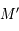 et
et 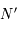 sont donc deux points distincts d'un cercle alignés avec le centre du cercle, ils sont donc diamétralement opposés.
sont donc deux points distincts d'un cercle alignés avec le centre du cercle, ils sont donc diamétralement opposés.
-
Question 8
Solution :
Le point 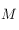 se trouvant sur l'horizon céleste, on a
se trouvant sur l'horizon céleste, on a 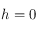 . La déclinaison étant dans l'intervalle
. La déclinaison étant dans l'intervalle ![[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation233.png) , elle est complètement déterminée par son sinus. Ainsi en utilisant la 4ème relation des équations données dans le préambule, on obtient:
, elle est complètement déterminée par son sinus. Ainsi en utilisant la 4ème relation des équations données dans le préambule, on obtient: 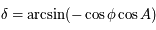 , où la fonction
, où la fonction 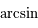 est la réciproque de la fonction sinus. Comme cette fonction est à valeur dans
est la réciproque de la fonction sinus. Comme cette fonction est à valeur dans ![[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation236.png) ,
, 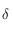 est complètement déterminé par cette relation.
est complètement déterminé par cette relation.

Connaissant 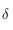 , la 5ème relation des équations données dans le préambule, nous permet d'avoir
, la 5ème relation des équations données dans le préambule, nous permet d'avoir 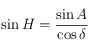 . Cette relation n'est pas définie pour les pôles (
. Cette relation n'est pas définie pour les pôles (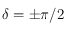 ), mais dans ce cas l'angle horaire
), mais dans ce cas l'angle horaire 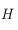 n'est pas définie non plus. D'autre part, on sait que la projection du pôle céleste nord est le centre de la sphère
n'est pas définie non plus. D'autre part, on sait que la projection du pôle céleste nord est le centre de la sphère 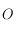 , alors que le pôle céleste sud est le seul point de la sphère céleste pour lequel la projection n'est pas définie.
, alors que le pôle céleste sud est le seul point de la sphère céleste pour lequel la projection n'est pas définie.
Soit 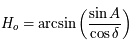 . On sait que
. On sait que ![H_o\in[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation246.png) , alors que
, alors que 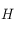 est dans l'intervalle
est dans l'intervalle ![[0, 2\pi]](../pages_trigo/equations_trigo/equation248.png) . Mais on sait que
. Mais on sait que 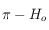 est aussi solution de l'équation pour
est aussi solution de l'équation pour 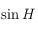 . Pour choisir quelle est la bonne solution, on doit utiliser la 6ème relation des équations données dans le préambule, qui nous permet d'avoir
. Pour choisir quelle est la bonne solution, on doit utiliser la 6ème relation des équations données dans le préambule, qui nous permet d'avoir 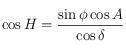 . Mais seul le signe de cette quantité nous intéresse puisque
. Mais seul le signe de cette quantité nous intéresse puisque 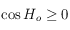 , alors que
, alors que 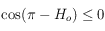 . Or comme
. Or comme ![\delta\in]-\pi/2,\pi/2[](../pages_trigo/equations_trigo/equation254.png) (les pôles sont exclus),
(les pôles sont exclus), 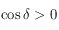 . Ainsi si
. Ainsi si 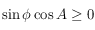 , on prend
, on prend 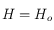 si
si 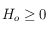 et
et 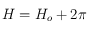 (qui est toujours solution, par périodicité, des deux équations que
(qui est toujours solution, par périodicité, des deux équations que 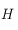 doit vérifier) si
doit vérifier) si 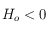 . Et si
. Et si 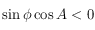 , on prend
, on prend 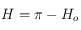 si
si 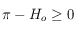 et
et 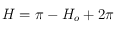 si
si 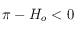 .
.
-
Question 9
Solution :
Un méridien étant un demi-grand cercle passant par les pôles du cercle de référence, comme les deux méridiens en question sont opposés l'un à l'autre par rapport à l'axe des pôles (ici l'axe zénith-nadir), ils forment à eux deux un grand cercle de 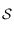 . Comme c'est un grand cercle son rayon est
. Comme c'est un grand cercle son rayon est 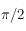 (en tant que cercle de
(en tant que cercle de 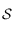 ). Son centre, sur la sphère, se trouve donc sur l'axe des pôles du grand cercle. Cette axe est perpendiculaire au plan contenant le grand cercle et il passe par le centre de la sphère, il est donc compris dans le plan de l'horizon céleste et est perpendiculaire à la droite d'intersection entre le grand cercle défini par les méridiens et l'horizon céleste. On en déduit que son azimut est égal à
). Son centre, sur la sphère, se trouve donc sur l'axe des pôles du grand cercle. Cette axe est perpendiculaire au plan contenant le grand cercle et il passe par le centre de la sphère, il est donc compris dans le plan de l'horizon céleste et est perpendiculaire à la droite d'intersection entre le grand cercle défini par les méridiens et l'horizon céleste. On en déduit que son azimut est égal à 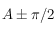 (deux solutions possibles).
(deux solutions possibles).
-
Question 10
Solution :
écliptique
Coordonnées équatorial du pôle de l'écliptique.
La déclinaison de 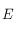 est tout simplement
est tout simplement 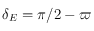 . Son ascension droite est
. Son ascension droite est 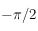 , ainsi d'après la relation donnée dans le préambule reliant l'ascension droite, le temps universel et l'angle horaire ,on voit que l'angle horaire de
, ainsi d'après la relation donnée dans le préambule reliant l'ascension droite, le temps universel et l'angle horaire ,on voit que l'angle horaire de 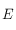 est
est 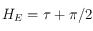 .
.
-
Question 11
Solution :
C'est tout simplement la projection du cercle de 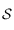 , centré en
, centré en 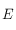 et de rayon
et de rayon 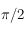 .
.
-
Question 12
Solution :
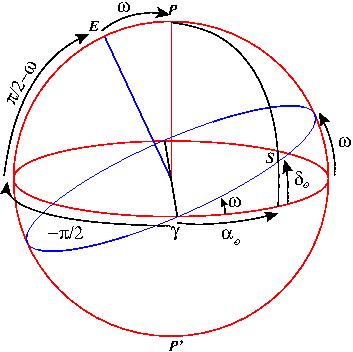
On utilise le triangle sphérique défini par le point vernal, noté 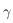 , le Soleil et le point d'intersection entre le méridien équatorial passant par le Soleil et l'équateur céleste. On a ainsi le triangle sphérique suivant:
, le Soleil et le point d'intersection entre le méridien équatorial passant par le Soleil et l'équateur céleste. On a ainsi le triangle sphérique suivant:
triangle sphérique pour le Soleil
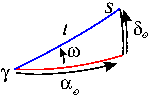
En appliquant les formules à ce triangle on obtient:
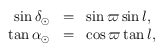
où 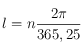 avec
avec 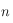 égal au nombre de jours écoulés depuis le 22 mars (le nombre de jours dans une année étant égale à 365,25) et le symbole
égal au nombre de jours écoulés depuis le 22 mars (le nombre de jours dans une année étant égale à 365,25) et le symbole  se réfère au Soleil.
se réfère au Soleil.
Comme ![\delta_\odot\in[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation298.png) , sa valeur est complètement déterminée par l'inversion de la première équation.
, sa valeur est complètement déterminée par l'inversion de la première équation.
Pour 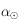 , si
, si 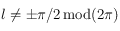 alors
alors ![\alpha_o=\tan^{-1}(\cos \varpi \tan l) \in ]-\pi/2,\pi/2[](../pages_trigo/equations_trigo/equation301.png) est solution de la deuxième équation, ainsi que
est solution de la deuxième équation, ainsi que 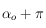 . Mais en remarquant que si
. Mais en remarquant que si 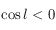 alors
alors 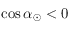 , on en déduit que si
, on en déduit que si 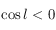 alors
alors 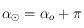 , sinon
, sinon 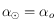 . Si
. Si 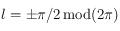 alors
alors 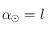 . On prendra bien soin ensuite de transformer
. On prendra bien soin ensuite de transformer 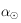 en un angle compris dans l'intervalle
en un angle compris dans l'intervalle ![[0,2\pi]](../pages_trigo/equations_trigo/equation311.png) .
.
L'angle horaire du Soleil est alors donné par l'équation du temps sidéral donnée dans le préambule :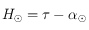 .
.
 Fin de la construction
Fin de la construction
La fin de la construction de l'astrolabe consiste simplement à placer le début de chaque mois sachant que chaque début correspond à une position spécifique du Soleil, ainsi que différentes étoiles dont les coordonnées équatoriales sont connues.
Pour l'animation, le temps universel est un paramètre d'entrée. Dans la pratique c'est plutôt l'angle horaire du Soleil qui est utilisé, l'astrolabe permet alors d'en déduire le temps universel.
-
Question 1
Solution :
horizon céleste
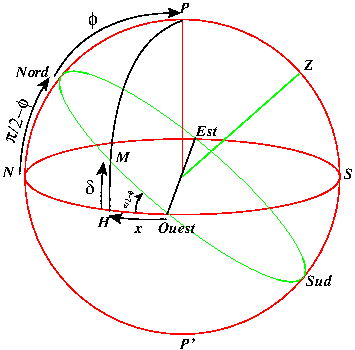
Horizon céleste (en vert) par rapport à l'équateur céleste (grand cercle Est, S, Ouest, N, en rouge).
-
Question 2
Solution :
On note 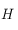 le point d'intersection entre le méridien équatorial passant par
le point d'intersection entre le méridien équatorial passant par 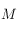 et l'équateur céleste. On considère le triangle sphérique
et l'équateur céleste. On considère le triangle sphérique 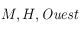 . Dans ce triangle, l'angle en
. Dans ce triangle, l'angle en 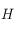 est égal à
est égal à 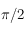 , et l'angle en Ouest est égal à la colatitude
, et l'angle en Ouest est égal à la colatitude 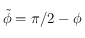 . On applique la formule ci-dessus avec
. On applique la formule ci-dessus avec 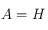 , et
, et 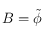 . On obtient :
. On obtient : 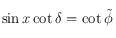 , soit
, soit 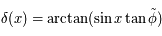 .
.
-
Question 3
Solution :
On a 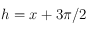 , c'est-à-dire
, c'est-à-dire 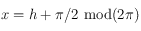 , ainsi :
, ainsi :
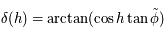
-
Question 4
Solution :
Avant tout, on remarque que la fonction 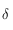 n'est pas définie si
n'est pas définie si 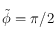 . On rappelle que
. On rappelle que 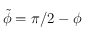 , comme
, comme ![\phi\in[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation359.png) ,
c'est bien la seule valeur interdite pour
,
c'est bien la seule valeur interdite pour 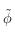 . Cette valeur correspond donc à
. Cette valeur correspond donc à 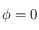 , c'est-à-dire à un point de l'équateur terrestre.
, c'est-à-dire à un point de l'équateur terrestre.
Pour tout autre latitude, 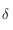 est définie, continue et dérivable sur
est définie, continue et dérivable sur 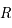 . On remarque que
. On remarque que 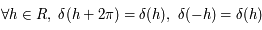 donc la fonction
donc la fonction 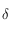 est
est 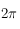 périodique et paire. En outre on a aussi
périodique et paire. En outre on a aussi 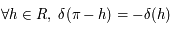 , ainsi le point de coordonnée
, ainsi le point de coordonnée 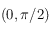 est un centre de symétrie pour la courbe représentative de
est un centre de symétrie pour la courbe représentative de 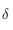 .
.
Il suffit donc d'étudier 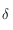 pour
pour ![h\in[0,\pi/2]](../pages_trigo/equations_trigo/equation371.png) .
.
On a : 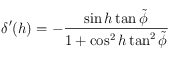 , ainsi le tableau de variation de
, ainsi le tableau de variation de 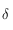 sur
sur ![[0,\pi/2]](../pages_trigo/equations_trigo/equation374.png) est:
est:
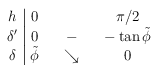
Ceci permet de tracer la courbe représentative de 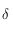 entre
entre ![[0,\pi/2]](../pages_trigo/equations_trigo/equation377.png) , puis on complète par symétrie centrale par rapport au point de coordonnées
, puis on complète par symétrie centrale par rapport au point de coordonnées 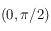 , puis par symétrie axiale par rapport à l'axe des ordonnées, ce qui permet de tracer la courbe entre
, puis par symétrie axiale par rapport à l'axe des ordonnées, ce qui permet de tracer la courbe entre ![[-\pi,0]](../pages_trigo/equations_trigo/equation379.png) . On obtient alors la courbe entre
. On obtient alors la courbe entre ![[0,2\pi]](../pages_trigo/equations_trigo/equation380.png) en utilisant la périodicité de
en utilisant la périodicité de 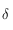 .
.
-
Question 5
Solution :
ecliptique
Equateur céleste en rouge, et grand cercle de l'écliptique en bleu.
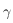
est la direction de l'équinoxe de printemps, c'est aussi l'origine des ascensions droites.
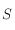
correspond à une position du Soleil sur l'écliptique,
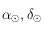
sont l'ascension droite et la déclinaison du Soleil, et
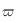
est l'obliquité.
-
Question 6
Solution :
En faisant le parallèle avec la figure de l'horizon céleste par rapport à l'équateur céleste, on a : 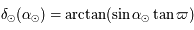 .
.
-
Question 7
Solution :
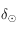 est définie continue dérivable sur
est définie continue dérivable sur  On a
On a 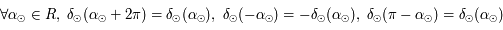 . Ainsi
. Ainsi 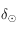 est
est 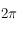 périodique, elle est impaire, et sa courbe représentative est symétrique par rapport à l'axe
périodique, elle est impaire, et sa courbe représentative est symétrique par rapport à l'axe 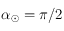 .
.
Ainsi, il suffit d'étudier 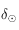 sur
sur ![[0,\pi/2]](../pages_trigo/equations_trigo/equation404.png) . On a
. On a 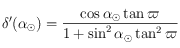 , ainsi le tableau de variation de
, ainsi le tableau de variation de  est :
est :
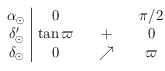
-
Question 8
Solution :
Pour l'équinoxe de printemps, le solstice d'été, l'équinoxe d'automne et le solstice d'hiver, on a respectivement  . Ainsi on a respectivement
. Ainsi on a respectivement 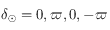 .
.
-
Question 9
Solution :
La date du jour permet de déterminer le nombre de jour écoulés depuis l'équinoxe de printemps (22 Mars environ). Ceci permet de connaître l'angle entre la direction du point vernal et le Soleil, mesuré sur l'écliptique. On note 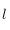 cet angle.
cet angle.
On utilise le triangle sphérique défini par le point vernal, noté 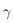 , le Soleil et le point d'intersection entre le méridien équatorial passant par le Soleil et l'équateur céleste. On a ainsi le triangle sphérique suivant :
, le Soleil et le point d'intersection entre le méridien équatorial passant par le Soleil et l'équateur céleste. On a ainsi le triangle sphérique suivant :
triangle sphérique pour le Soleil

En appliquant les formules à ce triangle on obtient:
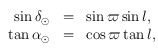
où 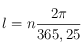 avec
avec 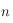 égal au nombre de jours écoulés depuis le 22 mars (le nombre de jours dans une année étant égal à 365,25) et le symbole
égal au nombre de jours écoulés depuis le 22 mars (le nombre de jours dans une année étant égal à 365,25) et le symbole  se réfère au Soleil.
se réfère au Soleil.
Pour 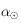 , si
, si 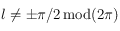 alors
alors ![\alpha_o=\arctan(\cos \varpi \tan l) \in ]-\pi/2,\pi/2[](../pages_trigo/equations_trigo/equation425.png) est solution de la deuxième équation, ainsi que
est solution de la deuxième équation, ainsi que  . Mais en remarquant que si
. Mais en remarquant que si 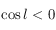 alors
alors 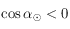 , on en déduit que si
, on en déduit que si 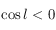 alors
alors 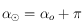 , sinon
, sinon 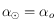 . Si
. Si 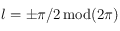 alors
alors 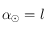 . On prendra bien soin ensuite de transformer
. On prendra bien soin ensuite de transformer 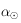 en un angle compris dans l'intervalle
en un angle compris dans l'intervalle ![[0,2\pi]](../pages_trigo/equations_trigo/equation435.png) .
.

 sphère céleste
sphère céleste![[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation1.png) donnant la hauteur au dessus d'un grand cercle de référence et en choisissant un côté positif (comme sur Terre, la latitude d'un lieu correspond à une hauteur au-dessus de l'équateur, comptée positivement dans l'hémisphère nord). Ce cercle de référence permet de définir l'axe des pôles et les pôles. La longitude correspond à l'angle, compris dans l'intervalle
donnant la hauteur au dessus d'un grand cercle de référence et en choisissant un côté positif (comme sur Terre, la latitude d'un lieu correspond à une hauteur au-dessus de l'équateur, comptée positivement dans l'hémisphère nord). Ce cercle de référence permet de définir l'axe des pôles et les pôles. La longitude correspond à l'angle, compris dans l'intervalle ![[0,2\pi]](../pages_trigo/equations_trigo/equation2.png) , entre un méridien de référence et le méridien passant par le point considéré. Cet angle est mesuré sur le cercle de référence en choisissant un sens positif.
Sur la Terre les longitudes sont mesurées à partir du méridien passant par Greenwich en prenant comme sens positif la direction de l'Ouest (ce qui correspond au sens des aiguilles d'une montre lorsqu'on regarde du pôle nord).
, entre un méridien de référence et le méridien passant par le point considéré. Cet angle est mesuré sur le cercle de référence en choisissant un sens positif.
Sur la Terre les longitudes sont mesurées à partir du méridien passant par Greenwich en prenant comme sens positif la direction de l'Ouest (ce qui correspond au sens des aiguilles d'une montre lorsqu'on regarde du pôle nord).
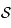 est une sphère de rayon unité (arbitraire), centrée sur l'observateur. Sur cette sphère on projette l'équateur terrestre, ce qui nous donne un grand cercle , appelé équateur céleste, le pôle nord se projette au point
est une sphère de rayon unité (arbitraire), centrée sur l'observateur. Sur cette sphère on projette l'équateur terrestre, ce qui nous donne un grand cercle , appelé équateur céleste, le pôle nord se projette au point 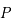 et le pôle sud au point
et le pôle sud au point 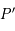 , appelés respectivement pôle céleste nord et pôle céleste sud.
, appelés respectivement pôle céleste nord et pôle céleste sud.
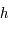 et positive au dessus de l'horizon, et une longitude mesurée sur l'horizon céleste, appelée azimut et notée
et positive au dessus de l'horizon, et une longitude mesurée sur l'horizon céleste, appelée azimut et notée 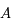 , en prenant comme méridien d'origine celui passant par le pôle céleste sud et comme sens positif vers l'ouest.
, en prenant comme méridien d'origine celui passant par le pôle céleste sud et comme sens positif vers l'ouest. 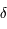 , positive vers le pôle céleste nord, et une longitude appelée angle horaire et noté
, positive vers le pôle céleste nord, et une longitude appelée angle horaire et noté 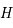 , avec comme méridien d'origine le méridien passant par le zénith et comme sens positif vers l'ouest.
, avec comme méridien d'origine le méridien passant par le zénith et comme sens positif vers l'ouest.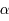 , est mesurée par rapport au méridien d'origine qui contient la position du Soleil au moment de l'équinoxe de printemps et le sens positif est le sens trigonométrique (vue du pôle nord). Cette position est appelé le point vernal et ce sens positif correspond au sens du mouvement annuel du Soleil.
, est mesurée par rapport au méridien d'origine qui contient la position du Soleil au moment de l'équinoxe de printemps et le sens positif est le sens trigonométrique (vue du pôle nord). Cette position est appelé le point vernal et ce sens positif correspond au sens du mouvement annuel du Soleil.
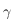 correspond à la direction du point vernal.
correspond à la direction du point vernal.
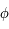 on a alors les équations suivantes permettant de passer d'un ensemble de coordonnées à l'autre:
on a alors les équations suivantes permettant de passer d'un ensemble de coordonnées à l'autre:
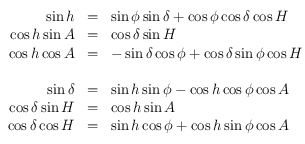
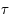 . On a la relation :
. On a la relation : 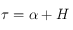 .
.

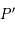 . Un point
. Un point 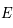 de la sphère aura pour image, le point
de la sphère aura pour image, le point 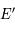 intersection de la droite
intersection de la droite 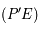 avec le plan
avec le plan 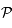 passant par le centre de la sphère
passant par le centre de la sphère 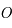 et perpendiculaire à la droite
et perpendiculaire à la droite 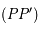 reliant les pôles. La figure suivante illustre cette projection.
reliant les pôles. La figure suivante illustre cette projection.
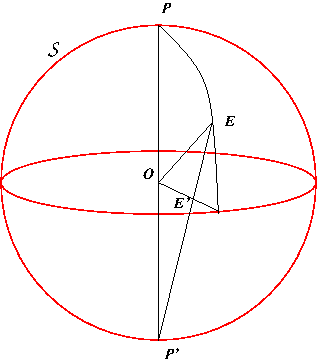
 .
.
 ? Quelles sont les points invariants par cette projection ?
? Quelles sont les points invariants par cette projection ?
 , centré en
, centré en 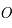 , l'axe des abscisses est dirigé vers l'origine des angles horaires sur l'équateur céleste et l'axe des ordonnées fait un angle de
, l'axe des abscisses est dirigé vers l'origine des angles horaires sur l'équateur céleste et l'axe des ordonnées fait un angle de 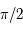 dans le sens trigonométrique vu du pôle céleste Sud. On utilisera alors un système de coordonnées polaires
dans le sens trigonométrique vu du pôle céleste Sud. On utilisera alors un système de coordonnées polaires 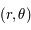 pour placer un point sur
pour placer un point sur 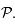
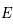 un point de
un point de 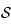 , de coordonnées
, de coordonnées 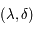 où
où 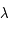 est l'angle horaire et
est l'angle horaire et 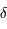 la déclinaison. Montrer que les coordonnées polaires de son image
la déclinaison. Montrer que les coordonnées polaires de son image 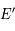 sont
sont 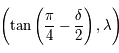 .
.
 qui contient aussi le point
qui contient aussi le point 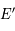 et le pôle céleste nord
et le pôle céleste nord 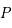 .
.
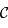 passant par le pôle céleste Sud
passant par le pôle céleste Sud 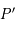 est une droite.
est une droite.
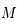 et
et 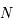 deux points de
deux points de 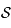 . Soit
. Soit 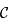 le cercle de
le cercle de 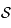 passant par ces points. On suppose que
passant par ces points. On suppose que 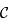 n'est pas un grand cercle. Il existe donc un cône de sommet
n'est pas un grand cercle. Il existe donc un cône de sommet 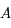 tangent à
tangent à 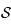 en
en 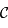 . Soit
. Soit 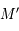 l'image de
l'image de 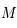 par projection sur
par projection sur 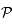 . La droite
. La droite 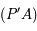 coupe le plan
coupe le plan 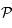 en
en 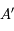 . Enfin, on appelle
. Enfin, on appelle  , le plan tangent à
, le plan tangent à 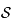 en
en 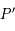 . La droite
. La droite 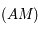 , coupe le plan
, coupe le plan  en
en 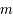 , et la droite
, et la droite 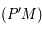 coupe le plan parallèle à
coupe le plan parallèle à  passant par
passant par 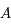 en
en 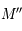 . La figure ci-dessous montre la construction.
. La figure ci-dessous montre la construction.
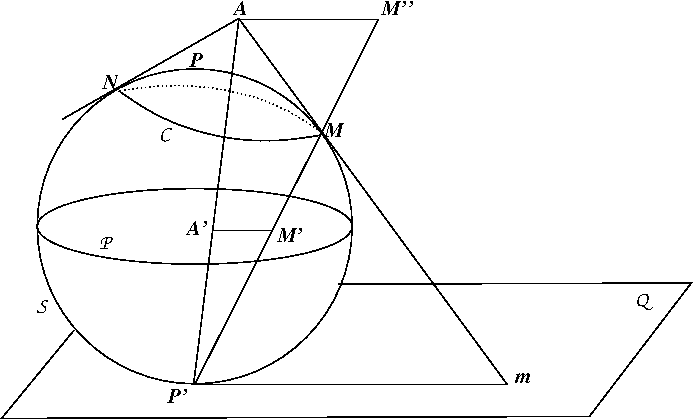
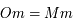 . En déduire que
. En déduire que 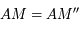 puis que
puis que 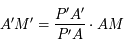 . En déduire que l'image de
. En déduire que l'image de 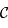 est un cercle.
est un cercle.
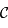 est un
est un 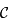 sont maintenant parallèles.
sont maintenant parallèles. 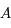 n'est plus défini, mais on peut encore construire le plan
n'est plus défini, mais on peut encore construire le plan  et le point
et le point 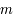 . On appelle
. On appelle 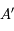 le point où la parallèle à
le point où la parallèle à 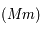 passant par
passant par 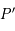 coupe la plan
coupe la plan 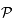 et
et 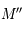 , le point où la droite
, le point où la droite 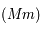 coupe le plan
coupe le plan 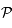 . Voir la figure ci-dessous.
. Voir la figure ci-dessous.
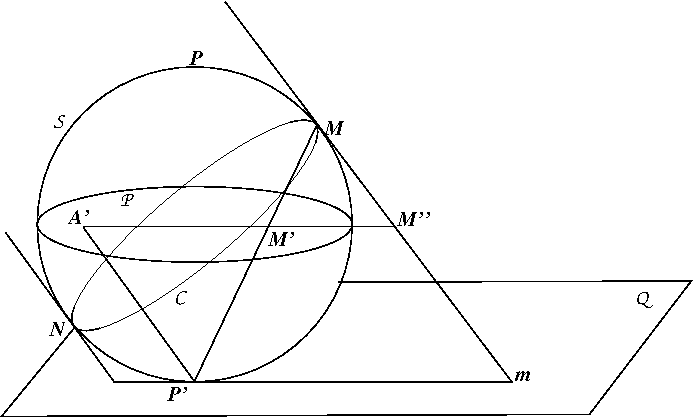
 . En déduire de nouveau que l'image de
. En déduire de nouveau que l'image de 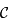 est un cercle.
est un cercle.
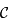 de
de 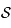 par son centre
par son centre 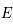 et son rayon
et son rayon 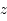 qui correspond en fait à l'angle sous lequel est vu le rayon depuis le centre
qui correspond en fait à l'angle sous lequel est vu le rayon depuis le centre 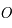 de la sphère
de la sphère 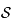 . On suppose que
. On suppose que ![z\in]0,\pi/2]](../pages_trigo/equations_trigo/equation162.png) . La figure ci-dessous illustre la situation.
. La figure ci-dessous illustre la situation.
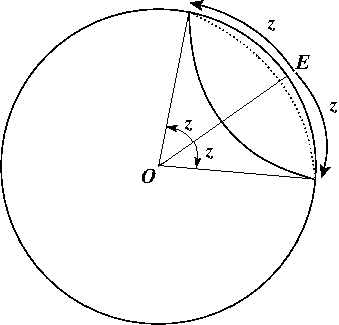
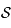 .
.
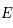 , ayant pour coordonnées horaires
, ayant pour coordonnées horaires 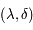 , et
, et 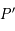 , coupant
, coupant 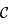 en
en 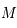 et
et 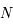 . Déterminer les coordonnées horaires de
. Déterminer les coordonnées horaires de 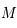 et
et 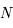 .
.
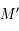 et
et 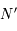 de
de 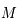 et
et 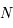 sont diamétralement opposées.
sont diamétralement opposées.
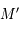 et
et 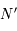 on peut déterminer le rayon et le centre du cercle projeté.
on peut déterminer le rayon et le centre du cercle projeté.
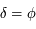 et
et 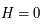 ). Ainsi, il est facile de tracer la projection de l'horizon puisqu'il correspond à un cercle de
). Ainsi, il est facile de tracer la projection de l'horizon puisqu'il correspond à un cercle de 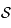 de centre
de centre 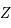 et de rayon
et de rayon 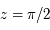 . De même différents cercles de hauteur constante
. De même différents cercles de hauteur constante 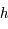 par rapport à l'horizon peuvent être obtenus en changeant la valeur de
par rapport à l'horizon peuvent être obtenus en changeant la valeur de 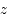 (on prend
(on prend 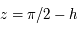 ).
).
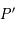 . Les projections correspondent donc à des demi-droites. On doit juste faire attention au fait qu'en astronomie le méridien d'origine par rapport à l'équateur correspond à celui qui contient le
. Les projections correspondent donc à des demi-droites. On doit juste faire attention au fait qu'en astronomie le méridien d'origine par rapport à l'équateur correspond à celui qui contient le 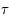 , varie dans le temps. Ainsi les projections des méridiens équatoriaux vont tourner en même temps que
, varie dans le temps. Ainsi les projections des méridiens équatoriaux vont tourner en même temps que 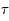 .
.
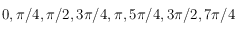 . On doit donc seulement calculer les coordonnées horaires de ces points pour pouvoir déterminer leur projection. Calculer donc les coordonnées horaires d'un point
. On doit donc seulement calculer les coordonnées horaires de ces points pour pouvoir déterminer leur projection. Calculer donc les coordonnées horaires d'un point 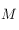 de l'horizon céleste d'azimut
de l'horizon céleste d'azimut 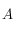 en un lieu de latitude
en un lieu de latitude 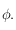
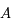 et le méridien d'azimut
et le méridien d'azimut 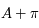 . Justifier que ces deux méridiens forment un grand cercle
. Justifier que ces deux méridiens forment un grand cercle 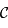 de
de 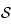 , dont on déterminera le centre sur
, dont on déterminera le centre sur 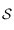 et le rayon. Ceci permet de construire facilement la projection des méridiens d'après ce qu'on a vu précédemment.
et le rayon. Ceci permet de construire facilement la projection des méridiens d'après ce qu'on a vu précédemment.
 . Les variations de l'obliquité sont tellement faibles qu'on peut la supposer constante ici. La droite d'intersection entre ces deux plans passe par le
. Les variations de l'obliquité sont tellement faibles qu'on peut la supposer constante ici. La droite d'intersection entre ces deux plans passe par le 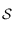 .
En s'aidant d'un dessin, déterminer les coordonnées équatoriales, puis les coordonnées horaires du pôle de l'écliptique
.
En s'aidant d'un dessin, déterminer les coordonnées équatoriales, puis les coordonnées horaires du pôle de l'écliptique 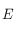 ayant une déclinaison positive.
ayant une déclinaison positive.
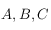 et de côté
et de côté 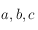 (
(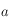 étant le côté opposé au sommet
étant le côté opposé au sommet 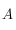 , etc.) où
, etc.) où 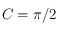 (voir la figure ci-dessous) :
(voir la figure ci-dessous) :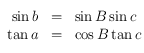 .
.

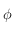 . Dessiner sur une sphère céleste avec l'équateur céleste comme plan de référence, le pôle céleste nord, l'horizon céleste, et les points cardinaux Sud, Ouest, Nord et Est. On notera aussi
. Dessiner sur une sphère céleste avec l'équateur céleste comme plan de référence, le pôle céleste nord, l'horizon céleste, et les points cardinaux Sud, Ouest, Nord et Est. On notera aussi 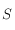 le point d'intersection du
le point d'intersection du 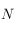 le point opposé à
le point opposé à 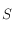 sur l'équateur céleste.
sur l'équateur céleste.

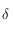 d'un point
d'un point 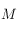 de l'horizon céleste, la latitude, la colatitude
de l'horizon céleste, la latitude, la colatitude 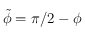 , et l'angle
, et l'angle 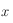 entre la direction ouest et le méridien équatorial passant par
entre la direction ouest et le méridien équatorial passant par 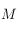 ,et compté positivement vers
,et compté positivement vers 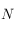 .
.
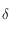 de
de 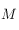 en fonction de
en fonction de 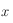 et
et 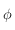 .
.
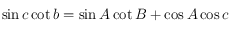 .
.
 , on souhaite utiliser un angle associé au Soleil, appelé heure solaire vraie et noté
, on souhaite utiliser un angle associé au Soleil, appelé heure solaire vraie et noté 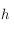 . Cet angle est mesuré sur l'équateur céleste, à partir de la direction
. Cet angle est mesuré sur l'équateur céleste, à partir de la direction 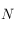 , et compté positivement vers l'Est.
Ainsi, l'Est,
, et compté positivement vers l'Est.
Ainsi, l'Est, 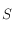 et l'Ouest correspondent respectivement à
et l'Ouest correspondent respectivement à 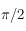 ,
, 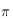 et
et 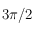 . Ecrire
. Ecrire 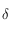 en fonction de
en fonction de 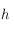 .
.
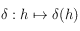 . On déterminera en particulier la valeur de
. On déterminera en particulier la valeur de 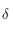 et de sa dérivée pour
et de sa dérivée pour 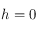 et
et 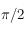 .
.
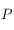 . L'angle entre ces deux directions est appelé obliquité est vaut
. L'angle entre ces deux directions est appelé obliquité est vaut 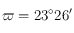 . Vu du pôle céleste nord, le Soleil décrit sa trajectoire dans le sens trigonométrique, c'est-à-dire que son ascension droite augmente au cours du temps.
. Vu du pôle céleste nord, le Soleil décrit sa trajectoire dans le sens trigonométrique, c'est-à-dire que son ascension droite augmente au cours du temps.
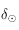 en fonction de
en fonction de 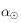 et de l'obliquité
et de l'obliquité 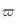 .
.
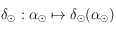 . On déterminera en particulier la valeur de
. On déterminera en particulier la valeur de 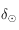 et de sa dérivée pour
et de sa dérivée pour 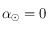 et
et 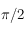 .
.
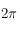 (en astronomie cependant on préfère noter les longitudes entre 0h et 24h).
(en astronomie cependant on préfère noter les longitudes entre 0h et 24h).
 et de côté
et de côté  (
(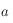 étant le côté opposé au sommet
étant le côté opposé au sommet 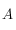 , etc.) où
, etc.) où  (voir la figure ci-dessous) :
(voir la figure ci-dessous) :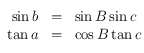 .
.
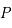 est le centre de la sphère
est le centre de la sphère 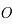 . L'ensemble des points invariants sont les points intersection de la sphère céleste
. L'ensemble des points invariants sont les points intersection de la sphère céleste 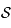 avec le plan
avec le plan 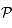 . C'est l'équateur céleste.
. C'est l'équateur céleste.
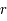 et
et 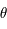 les coordonnées polaires de
les coordonnées polaires de 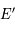 .
Le point
.
Le point 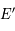 est dans demi-plan méridien passant par
est dans demi-plan méridien passant par 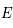 . Comme ce demi-plan permet de définir l'angle horaire
. Comme ce demi-plan permet de définir l'angle horaire 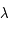 et que l'origine des angles horaires et des angles polaires dans
et que l'origine des angles horaires et des angles polaires dans 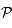 est la même, on a bien
est la même, on a bien 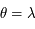 .
On se place alors dans le plan
.
On se place alors dans le plan 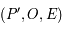 . Le triangle
. Le triangle 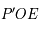 est isocèle en
est isocèle en 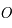 (voir la figure ci-dessous). Ainsi On en déduit que
(voir la figure ci-dessous). Ainsi On en déduit que 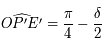 . Le triangle
. Le triangle 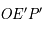 étant rectangle en
étant rectangle en 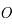 , on a donc:
, on a donc: 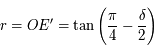 . On peut remarquer que cette formule est valable quelque soit
. On peut remarquer que cette formule est valable quelque soit ![\delta\in[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation59.png) .
.

 d'un point.
d'un point.
 le plan contenant le cercle
le plan contenant le cercle 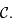 Comme
Comme 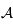 contient aussi
contient aussi 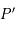 , on en déduit que les images des points de
, on en déduit que les images des points de 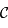 sont dans
sont dans 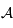 et par définition ils sont aussi dans
et par définition ils sont aussi dans 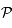 . L'intersection de deux plans étant une droite, on remarque que les images de
. L'intersection de deux plans étant une droite, on remarque que les images de 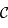 se trouvent bien sur une droite, notée
se trouvent bien sur une droite, notée 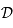 .
.
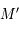 un point de
un point de 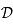 . La droite
. La droite 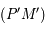 coupe le cercle
coupe le cercle 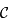 en un point
en un point 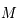 autre que
autre que 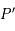 puisqu'elle n'est pas tangente à
puisqu'elle n'est pas tangente à 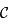 . Ainsi,
. Ainsi, 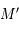 est l'image de
est l'image de 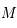 par la projection. Donc l'image de
par la projection. Donc l'image de 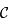 est la droite
est la droite 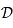 toute entière.
toute entière.
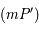 et
et 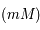 étant deux tangentes à
étant deux tangentes à 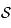 , on a bien
, on a bien 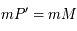 (facilement démontré en utilisant le théorème de Pythagore aux triangles
(facilement démontré en utilisant le théorème de Pythagore aux triangles 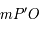 et
et 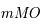 ). Les triangles
). Les triangles 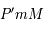 et
et 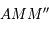 sont en configuration de Thales. Comme
sont en configuration de Thales. Comme 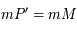 on a bien
on a bien 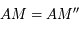 . De même, les triangles
. De même, les triangles 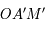 et
et 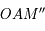 forment une autre configuration de Thales, donc :
forment une autre configuration de Thales, donc : 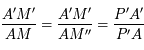 . Ainsi
. Ainsi 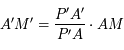 . Ainsi la distance
. Ainsi la distance 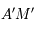 est indépendante de la position du point
est indépendante de la position du point 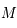 sur
sur 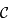 , tout comme l'est la distance
, tout comme l'est la distance 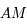 .
Donc le point
.
Donc le point 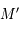 se trouve sur un cercle de centre
se trouve sur un cercle de centre 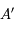 . On voit que tout le cercle est obtenu lorsque
. On voit que tout le cercle est obtenu lorsque 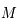 décrit
décrit 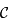 .
.
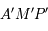 et
et 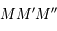 sont en configuration de Thales. On a donc:
sont en configuration de Thales. On a donc:
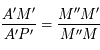 . Puis, avec la configuration de Thales des triangles
. Puis, avec la configuration de Thales des triangles 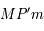 et
et 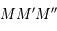 on a
on a 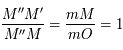 .
De nouveau on a bien l'image de
.
De nouveau on a bien l'image de 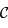 qui est un cercle de centre
qui est un cercle de centre 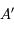 .
.
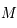 et
et 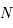 sont sur le même méridien que
sont sur le même méridien que 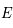 (ou sur le méridien opposé). Ainsi,
la latitude est obtenue à partir de celle de
(ou sur le méridien opposé). Ainsi,
la latitude est obtenue à partir de celle de 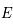 en ajoutant où en retranchant
en ajoutant où en retranchant 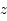 . Mais la latitude finale doit toujours être comprise dans l'intervalle
. Mais la latitude finale doit toujours être comprise dans l'intervalle ![[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation177.png) . Si elle est en dehors de cet intervalle alors, il faut prendre la latitude opposée et lui ajouter
. Si elle est en dehors de cet intervalle alors, il faut prendre la latitude opposée et lui ajouter 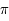 , et aussi prendre l'opposé de la longitude.
, et aussi prendre l'opposé de la longitude.

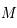 et
et 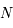 .
.
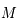 est obtenue en ajoutant
est obtenue en ajoutant 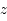 et
et 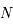 en retranchant
en retranchant 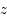 à
à 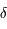 on a :
on a :
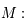
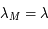 et
et 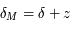 si
si 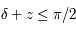 et
et
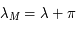 et
et 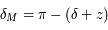 si
si 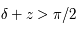 ,
,
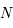 :
: 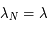 et
et 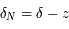 si
si 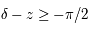 et
et
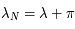 et
et 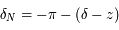 si
si 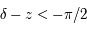 .
.
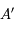 des constructions précédentes , et centre de la projection du cercle, se trouve dans le plan
des constructions précédentes , et centre de la projection du cercle, se trouve dans le plan 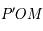 et dans le plan
et dans le plan 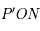 . Or ces deux plans sont confondus. Donc, les points
. Or ces deux plans sont confondus. Donc, les points 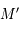 ,
, 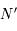 et
et 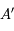 sont sur la droite intersection des plans
sont sur la droite intersection des plans 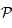 et
et 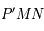 . Ils sont donc alignés.
. Ils sont donc alignés. 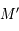 et
et 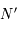 sont donc deux points distincts d'un cercle alignés avec le centre du cercle, ils sont donc diamétralement opposés.
sont donc deux points distincts d'un cercle alignés avec le centre du cercle, ils sont donc diamétralement opposés.
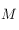 se trouvant sur l'horizon céleste, on a
se trouvant sur l'horizon céleste, on a 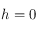 . La déclinaison étant dans l'intervalle
. La déclinaison étant dans l'intervalle ![[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation233.png) , elle est complètement déterminée par son sinus. Ainsi en utilisant la 4ème relation des équations données dans le
, elle est complètement déterminée par son sinus. Ainsi en utilisant la 4ème relation des équations données dans le 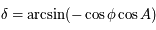 , où la fonction
, où la fonction 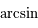 est la réciproque de la fonction sinus. Comme cette fonction est à valeur dans
est la réciproque de la fonction sinus. Comme cette fonction est à valeur dans ![[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation236.png) ,
, 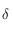 est complètement déterminé par cette relation.
est complètement déterminé par cette relation.

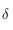 , la 5ème relation des équations données dans le
, la 5ème relation des équations données dans le 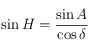 . Cette relation n'est pas définie pour les pôles (
. Cette relation n'est pas définie pour les pôles (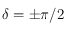 ), mais dans ce cas l'angle horaire
), mais dans ce cas l'angle horaire 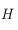 n'est pas définie non plus. D'autre part, on sait que la projection du pôle céleste nord est le centre de la sphère
n'est pas définie non plus. D'autre part, on sait que la projection du pôle céleste nord est le centre de la sphère 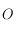 , alors que le pôle céleste sud est le seul point de la sphère céleste pour lequel la projection n'est pas définie.
, alors que le pôle céleste sud est le seul point de la sphère céleste pour lequel la projection n'est pas définie.
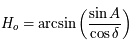 . On sait que
. On sait que ![H_o\in[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation246.png) , alors que
, alors que 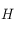 est dans l'intervalle
est dans l'intervalle ![[0, 2\pi]](../pages_trigo/equations_trigo/equation248.png) . Mais on sait que
. Mais on sait que 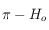 est aussi solution de l'équation pour
est aussi solution de l'équation pour 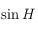 . Pour choisir quelle est la bonne solution, on doit utiliser la 6ème relation des équations données dans le
. Pour choisir quelle est la bonne solution, on doit utiliser la 6ème relation des équations données dans le 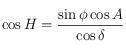 . Mais seul le signe de cette quantité nous intéresse puisque
. Mais seul le signe de cette quantité nous intéresse puisque 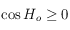 , alors que
, alors que 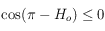 . Or comme
. Or comme ![\delta\in]-\pi/2,\pi/2[](../pages_trigo/equations_trigo/equation254.png) (les pôles sont exclus),
(les pôles sont exclus), 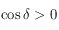 . Ainsi si
. Ainsi si 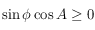 , on prend
, on prend 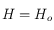 si
si 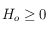 et
et 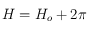 (qui est toujours solution, par périodicité, des deux équations que
(qui est toujours solution, par périodicité, des deux équations que 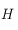 doit vérifier) si
doit vérifier) si 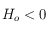 . Et si
. Et si 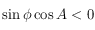 , on prend
, on prend 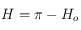 si
si 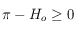 et
et 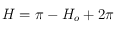 si
si 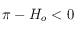 .
.
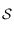 . Comme c'est un grand cercle son rayon est
. Comme c'est un grand cercle son rayon est 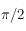 (en tant que cercle de
(en tant que cercle de  ). Son centre, sur la sphère, se trouve donc sur l'axe des pôles du grand cercle. Cette axe est perpendiculaire au plan contenant le grand cercle et il passe par le centre de la sphère, il est donc compris dans le plan de l'horizon céleste et est perpendiculaire à la droite d'intersection entre le grand cercle défini par les méridiens et l'horizon céleste. On en déduit que son azimut est égal à
). Son centre, sur la sphère, se trouve donc sur l'axe des pôles du grand cercle. Cette axe est perpendiculaire au plan contenant le grand cercle et il passe par le centre de la sphère, il est donc compris dans le plan de l'horizon céleste et est perpendiculaire à la droite d'intersection entre le grand cercle défini par les méridiens et l'horizon céleste. On en déduit que son azimut est égal à 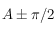 (deux solutions possibles).
(deux solutions possibles).

 est tout simplement
est tout simplement 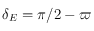 . Son ascension droite est
. Son ascension droite est 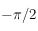 , ainsi d'après la relation donnée dans le
, ainsi d'après la relation donnée dans le 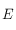 est
est 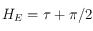 .
.
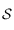 , centré en
, centré en 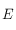 et de rayon
et de rayon 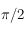 .
.
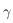 , le Soleil et le point d'intersection entre le méridien équatorial passant par le Soleil et l'équateur céleste. On a ainsi le triangle sphérique suivant:
, le Soleil et le point d'intersection entre le méridien équatorial passant par le Soleil et l'équateur céleste. On a ainsi le triangle sphérique suivant:

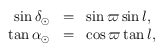
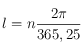 avec
avec 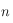 égal au nombre de jours écoulés depuis le 22 mars (le nombre de jours dans une année étant égale à 365,25) et le symbole
égal au nombre de jours écoulés depuis le 22 mars (le nombre de jours dans une année étant égale à 365,25) et le symbole  se réfère au Soleil.
se réfère au Soleil.
![\delta_\odot\in[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation298.png) , sa valeur est complètement déterminée par l'inversion de la première équation.
, sa valeur est complètement déterminée par l'inversion de la première équation.
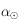 , si
, si 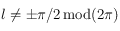 alors
alors ![\alpha_o=\tan^{-1}(\cos \varpi \tan l) \in ]-\pi/2,\pi/2[](../pages_trigo/equations_trigo/equation301.png) est solution de la deuxième équation, ainsi que
est solution de la deuxième équation, ainsi que 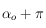 . Mais en remarquant que si
. Mais en remarquant que si 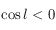 alors
alors 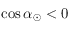 , on en déduit que si
, on en déduit que si 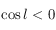 alors
alors 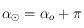 , sinon
, sinon 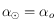 . Si
. Si 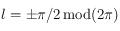 alors
alors 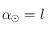 . On prendra bien soin ensuite de transformer
. On prendra bien soin ensuite de transformer 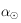 en un angle compris dans l'intervalle
en un angle compris dans l'intervalle ![[0,2\pi]](../pages_trigo/equations_trigo/equation311.png) .
.
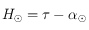 .
.

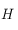 le point d'intersection entre le méridien équatorial passant par
le point d'intersection entre le méridien équatorial passant par 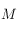 et l'équateur céleste. On considère le triangle sphérique
et l'équateur céleste. On considère le triangle sphérique 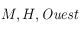 . Dans ce triangle, l'angle en
. Dans ce triangle, l'angle en 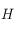 est égal à
est égal à 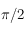 , et l'angle en Ouest est égal à la colatitude
, et l'angle en Ouest est égal à la colatitude 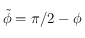 . On applique la formule ci-dessus avec
. On applique la formule ci-dessus avec 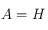 , et
, et 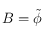 . On obtient :
. On obtient : 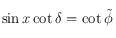 , soit
, soit 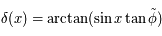 .
.
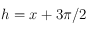 , c'est-à-dire
, c'est-à-dire 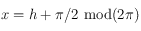 , ainsi :
, ainsi :
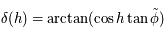
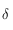 n'est pas définie si
n'est pas définie si 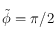 . On rappelle que
. On rappelle que 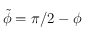 , comme
, comme ![\phi\in[-\pi/2,\pi/2]](../pages_trigo/equations_trigo/equation359.png) ,
c'est bien la seule valeur interdite pour
,
c'est bien la seule valeur interdite pour 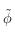 . Cette valeur correspond donc à
. Cette valeur correspond donc à 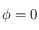 , c'est-à-dire à un point de l'équateur terrestre.
, c'est-à-dire à un point de l'équateur terrestre.
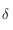 est définie, continue et dérivable sur
est définie, continue et dérivable sur 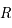 . On remarque que
. On remarque que 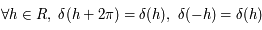 donc la fonction
donc la fonction 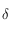 est
est 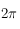 périodique et paire. En outre on a aussi
périodique et paire. En outre on a aussi 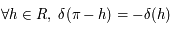 , ainsi le point de coordonnée
, ainsi le point de coordonnée 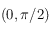 est un centre de symétrie pour la courbe représentative de
est un centre de symétrie pour la courbe représentative de 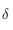 .
.
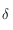 pour
pour ![h\in[0,\pi/2]](../pages_trigo/equations_trigo/equation371.png) .
.
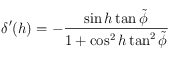 , ainsi le tableau de variation de
, ainsi le tableau de variation de 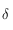 sur
sur ![[0,\pi/2]](../pages_trigo/equations_trigo/equation374.png) est:
est:

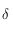 entre
entre ![[0,\pi/2]](../pages_trigo/equations_trigo/equation377.png) , puis on complète par symétrie centrale par rapport au point de coordonnées
, puis on complète par symétrie centrale par rapport au point de coordonnées 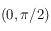 , puis par symétrie axiale par rapport à l'axe des ordonnées, ce qui permet de tracer la courbe entre
, puis par symétrie axiale par rapport à l'axe des ordonnées, ce qui permet de tracer la courbe entre ![[-\pi,0]](../pages_trigo/equations_trigo/equation379.png) . On obtient alors la courbe entre
. On obtient alors la courbe entre ![[0,2\pi]](../pages_trigo/equations_trigo/equation380.png) en utilisant la périodicité de
en utilisant la périodicité de 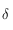 .
.

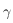 est la direction de l'équinoxe de printemps, c'est aussi l'origine des ascensions droites.
est la direction de l'équinoxe de printemps, c'est aussi l'origine des ascensions droites. 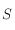 correspond à une position du Soleil sur l'écliptique,
correspond à une position du Soleil sur l'écliptique, 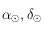 sont l'ascension droite et la déclinaison du Soleil, et
sont l'ascension droite et la déclinaison du Soleil, et 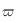 est l'obliquité.
est l'obliquité.
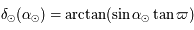 .
.
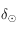 est définie continue dérivable sur
est définie continue dérivable sur  On a
On a 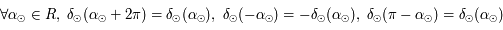 . Ainsi
. Ainsi 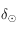 est
est 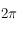 périodique, elle est impaire, et sa courbe représentative est symétrique par rapport à l'axe
périodique, elle est impaire, et sa courbe représentative est symétrique par rapport à l'axe 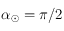 .
.
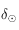 sur
sur ![[0,\pi/2]](../pages_trigo/equations_trigo/equation404.png) . On a
. On a 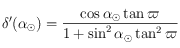 , ainsi le tableau de variation de
, ainsi le tableau de variation de 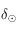 est :
est :
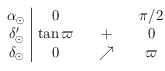
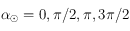 . Ainsi on a respectivement
. Ainsi on a respectivement 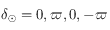 .
.
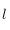 cet angle.
cet angle.
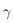 , le Soleil et le point d'intersection entre le méridien équatorial passant par le Soleil et l'équateur céleste. On a ainsi le triangle sphérique suivant :
, le Soleil et le point d'intersection entre le méridien équatorial passant par le Soleil et l'équateur céleste. On a ainsi le triangle sphérique suivant :
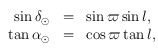
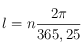 avec
avec 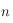 égal au nombre de jours écoulés depuis le 22 mars (le nombre de jours dans une année étant égal à 365,25) et le symbole
égal au nombre de jours écoulés depuis le 22 mars (le nombre de jours dans une année étant égal à 365,25) et le symbole  se réfère au Soleil.
se réfère au Soleil.
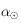 , si
, si 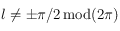 alors
alors ![\alpha_o=\arctan(\cos \varpi \tan l) \in ]-\pi/2,\pi/2[](../pages_trigo/equations_trigo/equation425.png) est solution de la deuxième équation, ainsi que
est solution de la deuxième équation, ainsi que  . Mais en remarquant que si
. Mais en remarquant que si 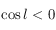 alors
alors 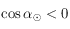 , on en déduit que si
, on en déduit que si 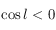 alors
alors 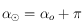 , sinon
, sinon 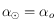 . Si
. Si 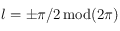 alors
alors 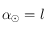 . On prendra bien soin ensuite de transformer
. On prendra bien soin ensuite de transformer 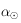 en un angle compris dans l'intervalle
en un angle compris dans l'intervalle ![[0,2\pi]](../pages_trigo/equations_trigo/equation435.png) .
.