Les ondes gravitationnelles générées par les mouvements de la matière
Pour mettre en vibration la surface d’un matelas, il faut des corps qui bougent dessus. Plus ils sont lourds et plus rapide est le mouvement, plus fortes seront les oscillations et plus facile sera leur détection. Dans l’Univers, l’exemple le plus extrême de corps massifs qui tournent à grande vitesse l’un autour de l’autre est fourni par les systèmes binaires de trous noirs massifs.
La courbure de l'espace-temps est plus grande quand la matière qui la génère est concentrée dans un petit volume
Une manière intuitive pour comprendre notre intérêt pour les trous noirs consiste à poser sur un matelas un grand livre d’art et une boule en bronze que nous avons choisie pour avoir exactement la même masse que le livre. La masse de la boule est distribuée sur une surface beaucoup plus petite que celle du livre, donc la pression sur les ressorts du matelas est plus forte, raison pour laquelle la boule de bronze s’enfoncera beaucoup plus dans le matelas que le livre d’art.
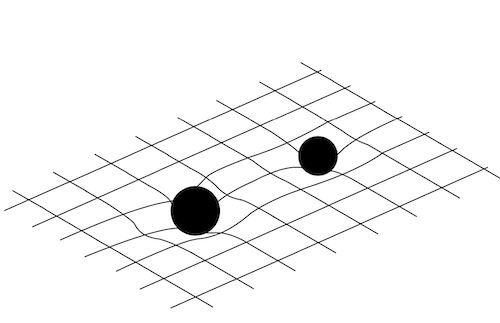
Courbure de l’espace-temps en présence de deux trois noirs. La déformation n’est pas statique parce que les trous noirs tournent autour de leur centre de masse commun . Donc elle se propage comme une vibration dans le tissu de l’espace-temps.
Les trous noirs plient l'espace-temps comme rien d'autre
Les trous noirs sont les corps les plus denses (ceux qui ont la plus grande masse par unité de volume). Donc, ils sont les plus aptes à courber l’espace-temps autour d’eux. La figure montre la courbure de l’espace-temps en présence de deux trous noirs. La déformation n’est pas statique parce que les trous noirs tournent autour de leur centre de masse commun. Donc elle se propage comme une vibration dans le tissu de l’espace-temps.
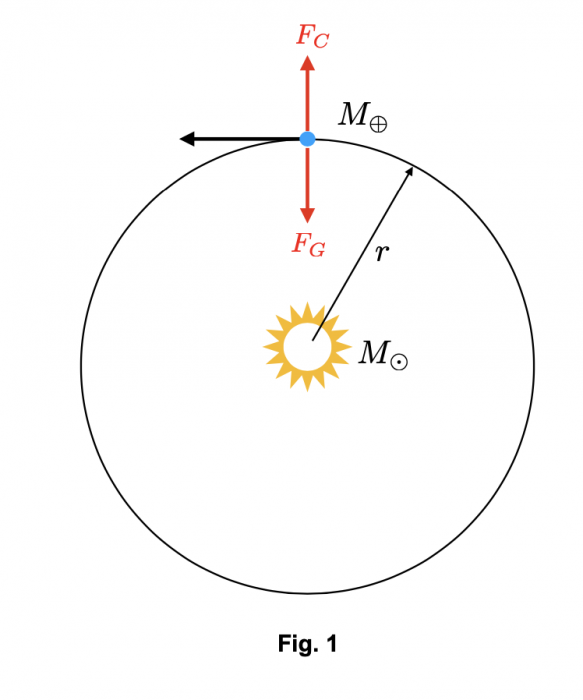
Le Soleil et la Terre : vitesse de rotation et temps orbital
Pour comprendre les systèmes binaires de trous noirs d’une manière plus quantitative, commençons par le cas, qui nous est beaucoup plus familier, du système Soleil-Terre (Fig. 1).
La vitesse à laquelle la Terre tourne autour du Soleil est déterminée par l’équilibre entre la force gravitationnelle 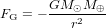 , qui pousse la Terre vers le Soleil, et la force centrifuge
, qui pousse la Terre vers le Soleil, et la force centrifuge 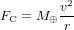 , qui pousse la Terre à s’en éloigner. Ici, G est la constante de gravitation universelle,
, qui pousse la Terre à s’en éloigner. Ici, G est la constante de gravitation universelle, 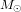 est la masse du Soleil,
est la masse du Soleil, 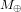 est la masse de la Terre, r est la distance entre la Terre et le Soleil, et v est la vitesse avec laquelle la Terre tourne autour du Soleil. La condition
est la masse de la Terre, r est la distance entre la Terre et le Soleil, et v est la vitesse avec laquelle la Terre tourne autour du Soleil. La condition 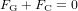 (si la Terre est sur une orbite circulaire, elle ne doit ni s’approcher du Soleil, ni s’en éloigner), donne :
(si la Terre est sur une orbite circulaire, elle ne doit ni s’approcher du Soleil, ni s’en éloigner), donne :
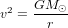 (1).
(1).
Le temps que la Terre prend pour faire un tour complet autour du Soleil (dit aussi la période orbitale) est donc :
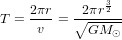 (2).
(2).
L'équation (2) n’exprime rien d’autre que la troisième loi de Kepler : le carré de la période de révolution T est proportionnel au cube du rayon orbital r.
En réalité, la Terre ne tourne pas autour du centre du Soleil, elle tourne autour du centre de masse du Système solaire, mais la masse du Système solaire est tellement dominée par celle du Soleil que l’on peut considérer que les deux sont la même chose.
Cela n’est pas le cas dans un système de deux corps (par exemple, deux trous noirs) de masse comparable. Les calculs sont donc plus compliqués, mais, à la fin, on retrouve l’équation (2) avec, au lieu de 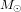 , la masse totale des deux trous corps : une période orbitale courte requiert des corps rapprochés et massifs.
, la masse totale des deux trous corps : une période orbitale courte requiert des corps rapprochés et massifs.
Trous noirs
L’équation (2) montre que des masses élevées et des corps très proches sont la clé pour avoir des oscillations avec une période courte. Le problème est que, normalement, les corps les plus massifs sont aussi les plus grands. Donc, si la masse est grande, il est difficile que r soit petit.
L’intérêt de considérer des trous noirs vient du fait que les trous noirs sont les corps les plus petits qui existent pour une masse donnée.
Pour comprendre pourquoi un trou noir est forcément petit (par rapport à sa masse), il faut revenir à l'équation (1). L'équation (1) nous donne la vitesse de rotation que la
Terre doit avoir pour tourner autour du Soleil sur une orbite circulaire. La vitesse de libération 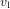 que la Terre devrait avoir pour s'affranchir de l'attraction du Soleil est un peu plus grande, mais pas beaucoup :
que la Terre devrait avoir pour s'affranchir de l'attraction du Soleil est un peu plus grande, mais pas beaucoup :
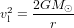 (3).
(3).
Ni  ni
ni 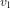 ne dépendent de
ne dépendent de 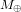 . Ceci est une manifestation du principe d'équivalence.
. Ceci est une manifestation du principe d'équivalence.
L'équation (3) montre que la vitesse de libération 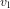 est plus grande quand r est plus petit. Bien entendu, r ne peut jamais être plus petit que la taille de l'objet qui produit l'attraction gravitationnelle. Le rayon
est plus grande quand r est plus petit. Bien entendu, r ne peut jamais être plus petit que la taille de l'objet qui produit l'attraction gravitationnelle. Le rayon
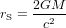 (4)
(4)
auquel 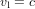 est appelé le rayon de Schwarzschild (c est la vitesse de la lumière). Dans l'équation (4), M est la masse du corps qui génère l'atttraction gravitationnelle. Ce corps n'a pas besoin d'être le Soleil.
est appelé le rayon de Schwarzschild (c est la vitesse de la lumière). Dans l'équation (4), M est la masse du corps qui génère l'atttraction gravitationnelle. Ce corps n'a pas besoin d'être le Soleil.
La masse du Soleil est 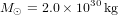 ;
; 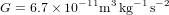 ; donc le rayon du Schwarzschild du Soleil vaut
; donc le rayon du Schwarzschild du Soleil vaut 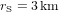 . Le Soleil a un rayon de 700000 km.
S'il était 230000 fois plus petit, tout en gardant la même masse, alors la vitesse de libération du Soleil serait plus grande que la vitesse de la lumière. Donc rien ne pourrait y échapper, même pas sa propre lumière. Si l'on cherche à observer un objet de masse
. Le Soleil a un rayon de 700000 km.
S'il était 230000 fois plus petit, tout en gardant la même masse, alors la vitesse de libération du Soleil serait plus grande que la vitesse de la lumière. Donc rien ne pourrait y échapper, même pas sa propre lumière. Si l'on cherche à observer un objet de masse 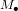 avec une taille :
avec une taille :
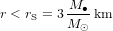 (5),
(5),
tout ce que l'on voit c'est ... un trou noir (Fig. 2), et c'est pour cela que l'on le dénote par le symbole  .
.

Fig. 2
Crédit :
NASA
La Fig. 2 montre la première image d'un trou noir, qui a été rendue publique le 10 avril 2019. Elle a été prise avec le Event Horizon Telescope, qui n'est pas, en réalité, un télescope, mais plutôt un réseau de radiotélescopes à différents endroits sur le globe terrestre. Le trou noir dans l'image se trouve au centre de M87, la galaxie elliptique géante au centre de l'amas de Virgo. Dans la Fig. 2, le trou noir correspond à la région centrale foncée ; la bouée orange est le gaz qui orbite autour du trou noir, avant d'être avalé.
En mai 2022, un deuxième trou noir, celui au centre de notre Galaxie, a été photographié par le même instrument.
La surface sphérique de rayon 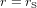 qui enveloppe un trou noir est dite l'horizon des évènements, parce que les évènements à son intérieur sont invisibles. Un trou noir ne peut pas déborder de son horizon ; autrement on verrait sa surface et ce ne serait pas un trou noir. En revanche, il n'y a aucune raison pour que la taille physique d'un trou nour ne puisse pas être plus petite que son horizon. Mais comme cette taille physique est impossible à connaître, c'est toujours le rayon de l'horizon que l'on utilise pour définir la taille d'un trou noir.
qui enveloppe un trou noir est dite l'horizon des évènements, parce que les évènements à son intérieur sont invisibles. Un trou noir ne peut pas déborder de son horizon ; autrement on verrait sa surface et ce ne serait pas un trou noir. En revanche, il n'y a aucune raison pour que la taille physique d'un trou nour ne puisse pas être plus petite que son horizon. Mais comme cette taille physique est impossible à connaître, c'est toujours le rayon de l'horizon que l'on utilise pour définir la taille d'un trou noir.
Crédit :
A. Cattaneo from NASA image
Période des ondes gravitationnelles pour un système de deux trous noirs
La distance minimale entre deux trous noirs est 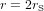 et correspond au cas de deux trous noirs en contact. Issue d'une simulation à l'ordinateur, la Fig. 3 montre deux trous noirs très proches l'un de l'autre, qui orbitent l'un autour de l'autre (le cercle blanc pointillé montre leur orbite autour du centre de masse du système binaire ). Si le deux trous noirs ont la même masse
et correspond au cas de deux trous noirs en contact. Issue d'une simulation à l'ordinateur, la Fig. 3 montre deux trous noirs très proches l'un de l'autre, qui orbitent l'un autour de l'autre (le cercle blanc pointillé montre leur orbite autour du centre de masse du système binaire ). Si le deux trous noirs ont la même masse 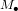 , la masse totale à insérer dans l'équation (2) est
, la masse totale à insérer dans l'équation (2) est 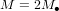 et la période orbitale vaut :
et la période orbitale vaut :
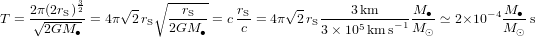 (6).
(6).
Pour un système de deux trous noirs en contact avec une masse identique de 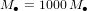 chacun (dans cet exemple, chaque trou noir a une masse égale à mille fois celle du Soleil), l’équation (6) donne
chacun (dans cet exemple, chaque trou noir a une masse égale à mille fois celle du Soleil), l’équation (6) donne 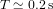 . Un tel système est suffisamment massif et compact pour produire des oscillations significatives dans la géométrie de l’espace-temps et il est capable de produire un signal avec une fréquence que l’on pourrait, à priori, mesurer avec des instruments de laboratoire.
. Un tel système est suffisamment massif et compact pour produire des oscillations significatives dans la géométrie de l’espace-temps et il est capable de produire un signal avec une fréquence que l’on pourrait, à priori, mesurer avec des instruments de laboratoire.
En réalité, le système binaire que nous avons décrit ne peut pas exister comme système stable dans la mécanique relativiste, parce que, à la différence du cas newtonien, dans lequel l’énergie est conservée, il perd de l’énergie par émission d’ondes gravitationnelles.
L’énergie que les trous noirs utilisent pour mettre en vibration l’espace-temps doit venir de quelque part. Elle vient de l'énergie cinétique de rotation des trous noirs eux-mêmes. Comme pour la révolution terrestre, les trous noirs sont maintenus sur un orbite circulaire l'un autour de l'autre par l'équilbre entre la force gravitationnelle et la force centrifuge. Si la force centrifuge diminue, parce que les trous noirs sont freinés par l'émission d'ondes gravitationnelles, alors la gravité va prévaloir, et les trous noirs se rapprochent jusqu’à tomber l’un sur l’autre.
Le processus accélère quand la distance entre les trous noirs diminue et l’émission d’ondes gravitationnelles devient plus importante. Une fois que la distance entre les trous noirs est comparable à la taille des trous noirs eux-mêmes, la coalescence se passe dans une fraction de seconde. Il s'ensuit que les ondes gravitationnelles générées par un système binaire de trous noirs ne sont détectables que pour un temps très court. Avant, le signal est trop faible. Après, il n’y a plus de signal parce qu’il n’y a qu’un seul trou noir.

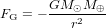 , qui pousse la Terre vers le Soleil, et la force centrifuge
, qui pousse la Terre vers le Soleil, et la force centrifuge 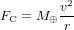 , qui pousse la Terre à s’en éloigner. Ici, G est la constante de gravitation universelle,
, qui pousse la Terre à s’en éloigner. Ici, G est la constante de gravitation universelle, 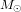 est la masse du Soleil,
est la masse du Soleil, 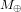 est la masse de la Terre, r est la distance entre la Terre et le Soleil, et v est la vitesse avec laquelle la Terre tourne autour du Soleil. La condition
est la masse de la Terre, r est la distance entre la Terre et le Soleil, et v est la vitesse avec laquelle la Terre tourne autour du Soleil. La condition 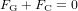 (si la Terre est sur une orbite circulaire, elle ne doit ni s’approcher du Soleil, ni s’en éloigner), donne :
(si la Terre est sur une orbite circulaire, elle ne doit ni s’approcher du Soleil, ni s’en éloigner), donne :
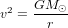 (1).
(1).
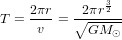 (2).
(2).
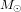 , la masse totale des deux trous corps : une période orbitale courte requiert des corps rapprochés et massifs.
, la masse totale des deux trous corps : une période orbitale courte requiert des corps rapprochés et massifs.
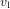 que la Terre devrait avoir pour s'affranchir de l'attraction du Soleil est un peu plus grande, mais pas beaucoup :
que la Terre devrait avoir pour s'affranchir de l'attraction du Soleil est un peu plus grande, mais pas beaucoup :
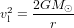 (3).
(3).
 ni
ni 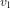 ne dépendent de
ne dépendent de 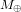 . Ceci est une manifestation du principe d'équivalence.
. Ceci est une manifestation du principe d'équivalence.
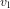 est plus grande quand r est plus petit. Bien entendu, r ne peut jamais être plus petit que la taille de l'objet qui produit l'attraction gravitationnelle. Le rayon
est plus grande quand r est plus petit. Bien entendu, r ne peut jamais être plus petit que la taille de l'objet qui produit l'attraction gravitationnelle. Le rayon
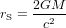 (4)
(4)
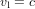 est appelé le rayon de Schwarzschild (c est la vitesse de la lumière). Dans l'équation (4), M est la masse du corps qui génère l'atttraction gravitationnelle. Ce corps n'a pas besoin d'être le Soleil.
est appelé le rayon de Schwarzschild (c est la vitesse de la lumière). Dans l'équation (4), M est la masse du corps qui génère l'atttraction gravitationnelle. Ce corps n'a pas besoin d'être le Soleil.
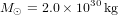 ;
; 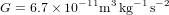 ; donc le rayon du Schwarzschild du Soleil vaut
; donc le rayon du Schwarzschild du Soleil vaut 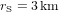 . Le Soleil a un rayon de 700000 km.
S'il était 230000 fois plus petit, tout en gardant la même masse, alors la vitesse de libération du Soleil serait plus grande que la vitesse de la lumière. Donc rien ne pourrait y échapper, même pas sa propre lumière. Si l'on cherche à observer un objet de masse
. Le Soleil a un rayon de 700000 km.
S'il était 230000 fois plus petit, tout en gardant la même masse, alors la vitesse de libération du Soleil serait plus grande que la vitesse de la lumière. Donc rien ne pourrait y échapper, même pas sa propre lumière. Si l'on cherche à observer un objet de masse 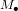 avec une taille :
avec une taille :
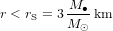 (5),
(5),
 .
.

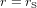 qui enveloppe un trou noir est dite l'horizon des évènements, parce que les évènements à son intérieur sont invisibles. Un trou noir ne peut pas déborder de son horizon ; autrement on verrait sa surface et ce ne serait pas un trou noir. En revanche, il n'y a aucune raison pour que la taille physique d'un trou nour ne puisse pas être plus petite que son horizon. Mais comme cette taille physique est impossible à connaître, c'est toujours le rayon de l'horizon que l'on utilise pour définir la taille d'un trou noir.
qui enveloppe un trou noir est dite l'horizon des évènements, parce que les évènements à son intérieur sont invisibles. Un trou noir ne peut pas déborder de son horizon ; autrement on verrait sa surface et ce ne serait pas un trou noir. En revanche, il n'y a aucune raison pour que la taille physique d'un trou nour ne puisse pas être plus petite que son horizon. Mais comme cette taille physique est impossible à connaître, c'est toujours le rayon de l'horizon que l'on utilise pour définir la taille d'un trou noir.

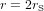 et correspond au cas de deux trous noirs en contact. Issue d'une simulation à l'ordinateur, la Fig. 3 montre deux trous noirs très proches l'un de l'autre, qui orbitent l'un autour de l'autre (le cercle blanc pointillé montre leur orbite autour du centre de masse du système binaire ). Si le deux trous noirs ont la même masse
et correspond au cas de deux trous noirs en contact. Issue d'une simulation à l'ordinateur, la Fig. 3 montre deux trous noirs très proches l'un de l'autre, qui orbitent l'un autour de l'autre (le cercle blanc pointillé montre leur orbite autour du centre de masse du système binaire ). Si le deux trous noirs ont la même masse 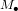 , la masse totale à insérer dans l'équation (2) est
, la masse totale à insérer dans l'équation (2) est 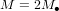 et la période orbitale vaut :
et la période orbitale vaut :
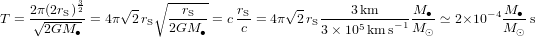 (6).
(6).
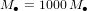 chacun (dans cet exemple, chaque trou noir a une masse égale à mille fois celle du Soleil), l’équation (6) donne
chacun (dans cet exemple, chaque trou noir a une masse égale à mille fois celle du Soleil), l’équation (6) donne 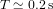 . Un tel système est suffisamment massif et compact pour produire des oscillations significatives dans la géométrie de l’espace-temps et il est capable de produire un signal avec une fréquence que l’on pourrait, à priori, mesurer avec des instruments de laboratoire.
. Un tel système est suffisamment massif et compact pour produire des oscillations significatives dans la géométrie de l’espace-temps et il est capable de produire un signal avec une fréquence que l’on pourrait, à priori, mesurer avec des instruments de laboratoire.