Des instruments d'optique
Auteur: Benjamin Mollier
- Introduction
- L'appareil photo
- L'appareil photo
- Description d'un appareil photo
- La focale d'un objectif
- Grand angulaire, téléobjectif
- Pourquoi voit-on plus gros un objet avec un téléobjectif ?
- Exercice : la focale équivalente
- Ouverture
- Exercices sur l'ouverture
- Profondeur de champ
- Résumé
- Exercice bilan : compact numérique
- L'oeil
- L'oeil
- Description
- Quelques caractéristiques de l'oeil
- Exercice : accomodation
- Accomodation
- Les défauts de vision
- Exercice : correction de la myopie
- Associations de lentilles (1)
- Associations de lentilles (2)
- Exercice bilan : correction de l'hypermétropie
- Résumé
- La loupe et l'oculaire
- L'oeil et la loupe
- L'intérêt d'une loupe, d'un oculaire
- Rappel sur l'angle apparent
- Exercice : angle apparent
- L'image d'un objet à travers une loupe
- Le grossissement
- Le grossissement commercial
- La puissance
- Latitude de mise au point
- L'oculaire
- Résumé
- La lunette astronomique
- La lunette astronomique
- Description de la lunette astronomique
- Principe de fonctionnement
- Grossissement
- Exercice : grossissement
- Champ d'une lunette astronomique
- Champ d'une lunette astronomique, démonstration
- Observer la Lune
- Diaphragme d'ouverture - Pupilles
- Diaphragme de champ - Lucarne
- Champ de pleine lumière - Champ de contour
- Résumé
- Exercice bilan : la grande lunette de Meudon
- Le télescope
- Le télescope
- Description d'un télescope
- Équivalence entre télescope et lunette
- Grossissement
- Les avantages du télescope (1)
- Les avantages du télescope (2)
- Les avantages et inconvénients en astronomie amateur
- Résumé
- Conclusion
Introduction
Il est maintenant temps d'utiliser ces miroirs et ces lentilles afin de construire des systèmes optiques.
 Différents types de systèmes optiques
Différents types de systèmes optiques
Tous les systèmes optiques n'ont pas nécessairement pour but de former des images. Certains n'ont pour fonction que de focaliser et transporter la lumière. Les phares par exemple. Nous ne nous intéresserons pas ici à de tels systèmes, et ne nous focaliserons (calembour) que sur ceux formant des images.
On peut distinguer 2 types de systèmes optiques :
- Les systèmes dit objectifs, qui forment directement une image sur un écran. Les rétro et vidéoprojecteurs, ou les appareils photos sont des systèmes objectifs.
- Les systèmes subjectifs, qui renvoient l'image à l'infini. On ne peut la voir apparaître sur un écran. Dans de tels systèmes, c'est l'oeil qui a pour but de former l'image. Le système subjectif a juste pour fonction de grossir l'image, d'en augmenter la luminosité. Les lunettes, les télescopes, les jumelles, les microscopes, et plus généralement tous les systèmes où on place notre oeil à la sortie d'un oculaire sont des systèmes subjectifs.
 Dans ce chapitre...
Dans ce chapitre...
... nous aborderons d'abord un système objectif : l'appareil photo. Il nous permettra d'introduire quelques notions d'optique comme le champ de vue, l'ouverture, la profondeur de champ.
Puis nous aborderons l'oeil et l'oculaire, préalables à l'étude de tous les systèmes subjectifs. On y introduira les notions de grossissement et de puissance.
Enfin, nous aborderons les systèmes subjectifs utilisés en astronomie : la lunette et le télescope.
 Prérequis
Prérequis
- Cadre de l'optique géométrique
- Rayon lumineux
- Objets et images réels et virtuels
- Objet à l'infini, diamètre apparent
- Stigmatisme et aplanétisme
- Lentilles minces
- Miroirs sphériques
Appareil photo

Crédit :
B. Mollier
Oeil
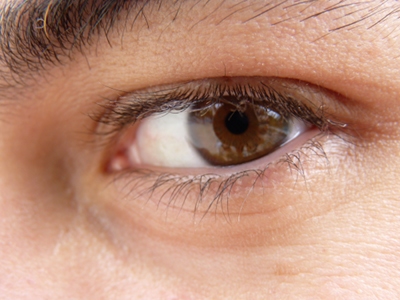
La deuxième section sera consacrée à
l'oeil.
Crédit :
A. Proust
L'oculaire

Crédit :
B. Mollier
Lunette astronomique

La quatrième section sera consacrée aux
lunettes.
Crédit :
B. Mollier
Télescope

Crédit :
B. Mollier
L'appareil photo
Auteur: Benjamin Mollier
L'appareil photo
Commençons donc par l'appareil photo. Pourquoi débuter par lui ? Car c'est un système optique très simple. Basiquement, c'est une lentille (l'objectif) placée devant un écran (le capteur ou la pellicule). C'est tout !
Modélisation d'un appareil photo
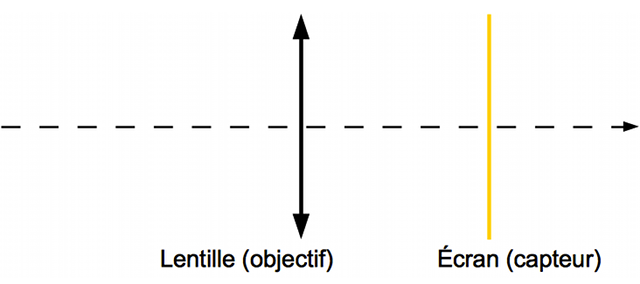
Un appareil photo peut être modélisé par une lentille placée devant un écran.
Crédit :
ASM/B. Mollier
Bon, je vous embobine un peu. Si on démonte un appareil photo, c'est beaucoup plus compliqué que ça. Mais la modélisation une lentille + un écran suffit largement pour comprendre son fonctionnement.
Description d'un appareil photo
Qu'est-ce qu'un appareil photo ? Je l'ai dit juste avant, c'est une lentille et un écran. Plus exactement, un objectif qui va former l'image du sujet sur notre capteur.
 Description d'un réflex
Description d'un réflex
Je vais brièvement décrire le boîtier réflex classique, avec objectif amovible et capteur 24x36.
L'objectif est un tube dans lequel on trouve un grand nombre de lentilles (parfois une dizaine). Elles servent à faire l'image du sujet sur le capteur, d'en faire la mise au point correcte, de zoomer éventuellement, et d'assurer une bonne correction des aberrations optiques et chromatiques. Je vous l'avais déjà dit, on ne travaille pas, en photo, dans les conditions de Gauss, car on perdrait trop de lumière.
On trouve aussi un diaphragme permettant de régler la quantité de lumière rentrant dans l'appareil (réglage de l'ouverture et de la profondeur de champ).
Dans le boîtier, on trouve un miroir basculant. Il renvoie la lumière vers le viseur pour permettre le cadrage, puis bascule pour la laisser rentrer dans la chambre pendant la prise de vue.
On trouve derrière l'obturateur, qui ne s'ouvre que pendant la prise de vue, pour laisser la lumière imprimer le capteur ou la pellicule. La quantité de lumière arrivant sur le capteur est bien sûr proportionnelle au temps d'exposition, c'est-à-dire la durée d'ouverture de l'obturateur.
Enfin, derrière l'obturateur, on trouve la pellicule sur les anciens appareils argentiques, ou un capteur CCD, sur les appareils photo numériques (abrégé APN). La dimension classique du capteur est (ou était) 24x36 mm. Même si elle n'est plus utilisée dans tous les APN, surtout les compacts, elle sert encore de référence pour les calculs de focale.
Par défaut, quand je parlerai d'APN, ce sera un réflex avec un capteur de 24x36 mm.
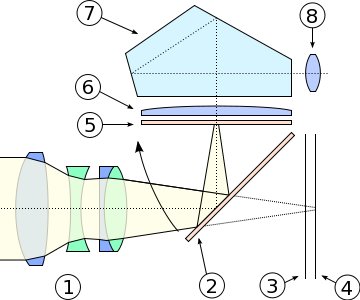
Coupe transversale d'un appareil photo reflex.
- 1. Objectif
- 2. Miroir abaissé (image visible dans l'oculaire / le viseur)
- 3. Obturateur focal
- 4. Capteur/Film
- 5. Verre dépoli
- 6. Condenseur
- 7. Pentaprisme
- 8. Oculaire/Viseur
Crédit :
Colin M.L. Burnett, GFDL/CC BY-SA 3.0
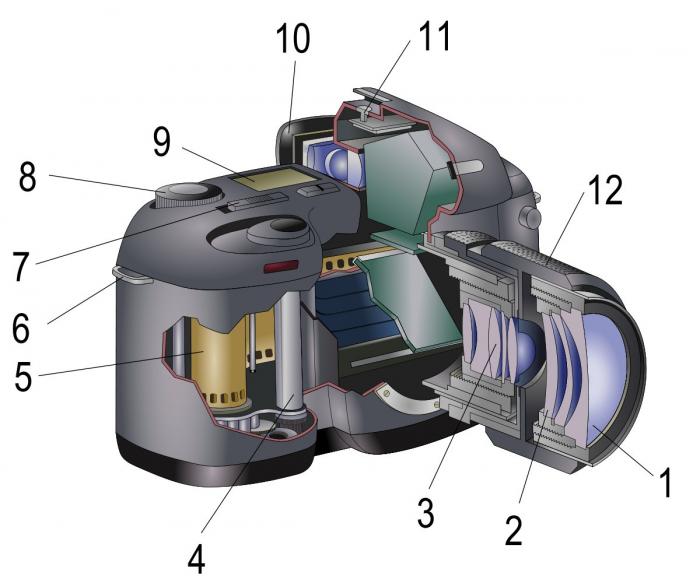
Coupe d'un appareil photo réflex
- 1. Lentille frontale de l'objectif
- 3. Diaphragme
- 4. Obturateur
- 5. Pellicule
- 10. Viseur
- 12. Bague de mise au point
La focale d'un objectif
Objectif à focale variable 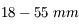 , téléobjectif de
, téléobjectif de 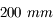 , grand angulaire de
, grand angulaire de 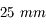 ... qu'est-ce que tout ça ?
... qu'est-ce que tout ça ?
Des chiffres ?

Que veulent dire ces chiffres
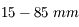
?
Crédit :
B. Mollier
Grand angulaire, téléobjectif
 Angle de champ
Angle de champ
La focale de l'objectif nous donne une information sur l'angle embrassé par l'appareil.
L'angle de champ est l'angle couvert par l'appareil photo. Si c'est angle est grand, on photographie une grande zone, un vaste paysage par exemple. S'il est petit, on ne photographie qu'un détail, par exemple un animal perdu dans le paysage.
 Lien entre angle de champ et focale
Lien entre angle de champ et focale
L'angle de champ et la focale sont reliés entre eux. Ils dépendent de la taille du capteur. La référence est le capteur de 24x36. S'il est de taille différente, on calculera des focales équivalentes ramenées au format 24x36 (cf page suivante).
Pour qu'une partie du paysage soit photographiée, il faut que son image arrive sur le capteur. Les bords du capteur définissent donc la limite de ce qui est photographiable. Ce dernier projette un cône virtuel en avant de l'appareil photo. Tout ce qui est dans ce cône apparaîtra lors de la soirée diapo. Ce qui est en dehors sera perdu à jamais...
La distance entre le capteur et l'objectif est typiquement la distance focale. On est donc en mesure de calculer l'angle de champ connaissant la taille du capteur et la focale.
Angle de champ
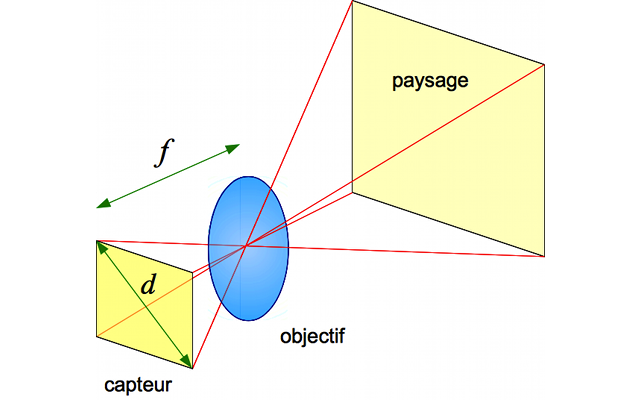
Crédit :
ASM/B. Mollier
Pour les curieux, son expression est 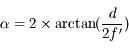 , où
, où 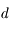 est la diagonale du capteur,
est la diagonale du capteur, 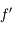 la focale.
la focale.
Angle de champ et focale
| Pour un capteur de 24x36 mm |
| Focale | Angle de champ (environ) |
| 17 mm | 105° |
| 28 mm | 75° |
| 35 mm | 65° |
| 50 mm | 45° |
| 80 mm | 30° |
| 105 mm | 23° |
| 135 mm | 18° |
| 200 mm | 12° |
| 300 mm | 8° |
 Grand angulaire, téléobjectif
Grand angulaire, téléobjectif
On classe les objectifs en 2 catégories. Les grands angulaires possédant une courte focale et un grand champ, et les téléobjectifs possédant une longue focale et un petit champ.
La limite entre les deux catégories est pour une focale d'environ 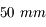 qui offre un champ comparable à celui d'un oeil humain.
qui offre un champ comparable à celui d'un oeil humain.
Grands angulaires et téléobjectifs
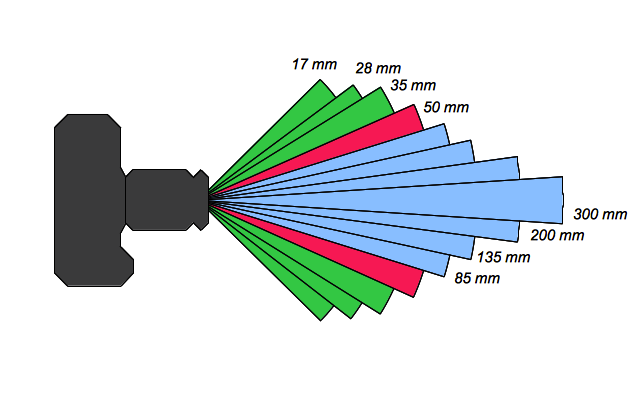
En vert, la classe des objectifs grand-angle, en bleu, celle des téléobjectifs. En rouge, l'objectif de
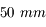
dont l'angle de champ est équivalent à celui de l'oeil.
Crédit :
ASM/B. Mollier
Objectif de 25 mm

Grande coupole de l'observatoire de Meudon prise avec un objectif de
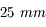
.
Crédit :
B. Mollier
Objectif de 70 mm

Grande coupole de l'observatoire de Meudon prise avec un objectif de
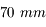
.
Crédit :
B. Mollier
Objectif de 120 mm

Grande coupole de l'observatoire de Meudon prise avec un objectif de
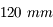
.
Crédit :
B. Mollier
Objectif de 300 mm

Grande coupole de l'observatoire de Meudon prise avec un objectif de
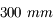
.
Crédit :
B. Mollier
Pourquoi voit-on plus gros un objet avec un téléobjectif ?
 Un gros zoom
Un gros zoom
Pourquoi voit-on plus gros un objet avec un téléobjectif ? un zoom dirons nous de manière abusive ?
L'angle de vue étant plus réduit, on met une portion de l'espace plus petite sur la même surface de capteur, on l'a agrandi.
Un arbre vu au grand angle et au téléobjectif
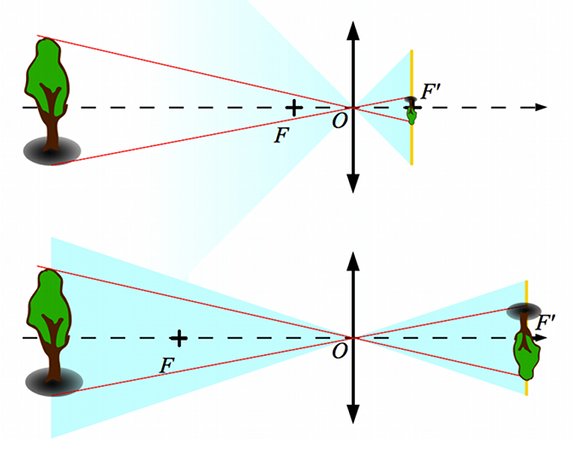
Plus la focale est longue, plus l'image d'un objet (l'arbre ici) est grande et prend de la place sur le capteur.
Crédit :
ASM/B. Mollier
Exercice : la focale équivalente
Auteur: Benjamin Mollier
 Focale équivalente
Focale équivalente
Difficulté : ☆☆
Temps : 20 min
Nous venons de voir que l'angle de champ dépend de la taille du capteur. Or, de nombreux APN possèdent maintenant des capteurs plus petits. Nous allons prendre l'exemple d'un APN du commerce (dont je ne citerai pas la marque) possédant un capteur mesurant 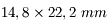 .
.
Boîtier avec petit capteur

Sur ce boîtier, le capteur est de petite taille. Il ne fait pas
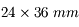
comme les argentiques, mais
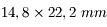
.
Crédit :
B. Mollier
Question 1)
J'adapte dessus un objectif de 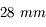 de focale. Rappelez quel serait l'angle de champ avec un capteur
de focale. Rappelez quel serait l'angle de champ avec un capteur 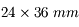 .
.
Question 2)
Quelle valeur prend cet angle avec notre capteur plus petit ?
Question 3)
Calculez quelle focale donnerait le même angle de champ avec un capteur 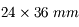 . C'est ce qu'on appellera la focale utile (ou équivalente).
. C'est ce qu'on appellera la focale utile (ou équivalente).
Question 4)
Calculer la focale utile sur notre nouveau boîtier si j'adapte un téléobjectif de 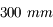 . Commentez.
. Commentez.
Question 5)
À l'inverse, si je désire obtenir une focale utile de 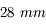 , quel objectif dois-je acheter ? Concluez.
, quel objectif dois-je acheter ? Concluez.
Ouverture
 Exposition
Exposition
L'exposition, en photographie, désigne la quantité de lumière, le nombre de photons, enregistré par le capteur.
Elle dépend de trois paramètres :
- Le temps de pose : il paraît évident que, plus on pose longtemps, plus on enregistre de photons.
- L'ouverture : plus notre objectif est large, plus il peut collecter de lumière.
- La sensibilité : plus le capteur, ou la pellicule, est sensible, plus la lumière est amplifiée.
Dans le cadre de ce cours d'optique, nous ne nous intéresserons qu'au cas de l'ouverture. De nombreux ouvrages consacrés à la photographie traitent du reste.
 L'ouverture
L'ouverture
S'il est un paramètre important en photographie, c'est bien l'ouverture. On contrôle cette quantité à l'aide d'un diaphragme. Plus on ferme le diaphragme, plus on diminue l'ouverture.
Si ce réglage a un impact direct sur la quantité de lumière qui rentre dans l'appareil, il en a aussi sur la qualité de la photo. Réduire l'ouverture augmente la zone de netteté de l'image (on parle de profondeur de champ), peut réduire certaines aberrations (en se rapprochant des conditions de Gauss), mais gare au vignétage !
Cette quantité s'exprime étrangement en 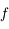 sur un nombre. Nous allons voir pourquoi.
sur un nombre. Nous allons voir pourquoi.
 Angle d'ouverture
Angle d'ouverture
L'angle d'ouverture 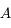 mesure le rapport entre le diamètre
mesure le rapport entre le diamètre 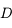 de l'objectif (du collecteur de lumière en général) et sa focale
de l'objectif (du collecteur de lumière en général) et sa focale 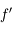 :
:
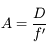
Angle d'ouverture
L'angle d'ouverture
mesure le rapport entre le diamètre
de l'objectif (du collecteur de lumière en général) et sa focale
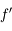
:
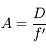
Crédit :
ASM/B. Mollier
 Attention
Attention
Ne pas confondre l'angle de champ, qui dépend de la taille du capteur, et l'angle d'ouverture, qui dépend du diamètre de l'objectif.
 Nombre d'ouverture
Nombre d'ouverture
Le nombre d'ouverture (noté N.O.) ou plus simplement ouverture est la quantité inverse 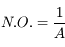
On la note 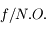
Par exemple, si je possède un objectif de 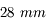 de focale, avec un diaphragme de
de focale, avec un diaphragme de 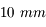 de diamètre, l'angle d'ouverture vaut
de diamètre, l'angle d'ouverture vaut 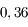 et son ouverture vaut 2,8. On parle donc d'objectif ouvert à
et son ouverture vaut 2,8. On parle donc d'objectif ouvert à 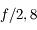 .
.
Plus le chiffre est petit, plus l'objectif est ouvert, plus la quantité de lumière qui rentre est importante. À l'inverse, plus ce chiffre est grand, plus l'objectif est fermé, et moins la quantité de lumière qui rentre est importante.
Pour résumer, un objectif ouvert à 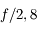 veut simplement dire que le diamètre du diaphragme est 2,8 fois plus petit que la focale.
veut simplement dire que le diamètre du diaphragme est 2,8 fois plus petit que la focale.
Exercices sur l'ouverture
 Ouverture
Ouverture
Question 1)
Je possède un téléobjectif de 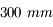 de focale, dont le diamètre est
de focale, dont le diamètre est 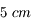 . Quelle pourra être l'ouverture maximale ?
. Quelle pourra être l'ouverture maximale ?
Profondeur de champ
 Profondeur de champ
Profondeur de champ
Nous avons vu, lors du cours sur les lentilles, qu'il n'existe qu'un seul plan antécédent du plan du détecteur. Autrement dit, notre photo ne sera nette qu'à une distance très précise de l'appareil photo.
Cependant, lorsque l'on regarde une photo, celle-ci nous apparaît nette sur une certaine distance, parfois très courte, parfois très grande.
Cette zone nette s'appelle la profondeur de champ. Plus celle-ci est grande, plus la photo sera nette longtemps. À l'inverse, plus la profondeur de champ est petite, plus courte sera la distance sur laquelle la photo sera nette.
Faible profondeur de champ

Avec une grande ouverture, la profondeur de champ est réduite. Les épis en arrière-plan sont flous.
Crédit :
B. Mollier
Faible profondeur de champ

Avec une faible ouverture, la profondeur de champ est augmentée. Les épis en arrière-plan sont cette fois-ci plus nets.
Crédit :
B. Mollier
 Lien avec l'ouverture
Lien avec l'ouverture
Si l'ouverture est importante, les rayons issus d'un point empruntent beaucoup de chemins différents. Si l'image de cet objet n'est pas sur le capteur, mais en avant ou en arrière, alors tous ces rayons tombent sur le capteur en une largeur zone, une grosse tache (regardez l'intersection des faisceaux avec le capteur dans l'image en bas). L'image est floue.
Mais si on réduit l'ouverture, on diminue le nombre de rayons entrant dans l'appareil, et on réduit ainsi la taille de la tache où ils convergent.
À la limite, si on ferme au maximum le diaphragme, on ne sélectionne plus qu'un seul rayon par point. L'image est alors nette à toutes les distances. On peut même se passer de la lentille. C'est le principe du sténopé. Par contre, comme très peu de lumière entre, il faut poser très longtemps.
Ouverture et profondeur de champ
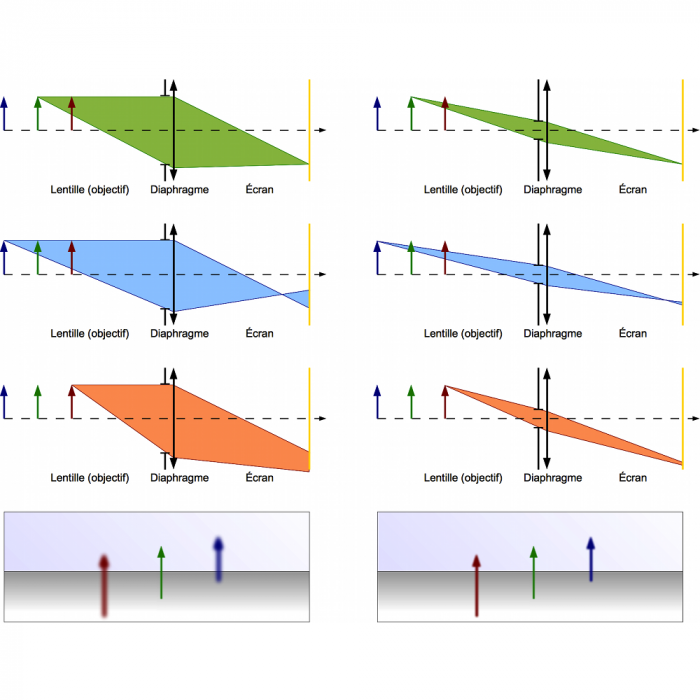
Plus l'ouverture est grande, plus la profondeur de champ est réduite. Premier plan et arrière plan sont flous. À l'inverse, plus on diminue l'ouverture, plus la profondeur de champ augmente. Premier plan et arrière plan apparaissent nets.
Crédit :
ASM/B. Mollier
Résumé
 Modélisation
Modélisation
L'appareil photo peut être modélisé par une simple lentille placée devant un écran.
 Focale
Focale
La focale d'un objectif est la distance focale de la lentille équivalente.
Une courte focale entraîne un grand angle de champ. Ce type d'objectif est appelé grand angle. Ces derniers possèdent une focale inférieure à 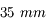 .
.
Une longue focale entraîne un angle de champ réduit. Ce type d'objectif est appelé téléobjectif. Ces derniers possèdent une focale supérieure à 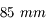 .
.
 Ouverture
Ouverture
L'ouverture mesure le rapport entre le diamètre du diaphragme et la focale.
Pour ouvrir un objectif, on ouvre le diaphragme : on augmente son diamètre. On augmente la quantité de lumière rentrant dans l'appareil, et on diminue la profondeur de champ.
En réduisant le diamètre du diaphragme, on ferme l'objectif. On réduit la quantité de lumière rentrant dans l'appareil, et on augmente la profondeur de champ.
Exercice bilan : compact numérique
Auteur: B. Mollier
 Compact numérique
Compact numérique
Ci-dessous, vous pouvez voir la photo d'un compact numérique. De nombreuses informations sont inscrites sur sa face avant. Que signifient-elles ?
Le compact numérique

Un appareil photo compact. Sur l'objectif, on peut lire plusieurs chiffres comme 1:3.3-4.9 / 4.1 - 49.2 ainsi que 25 mm WIDE.
Crédit :
B. Mollier
Question 1)
Vous pouvez lire sur l'objectif 25 mm WIDE, ainsi que 1:3.3-4.9 et enfin 4.1 - 49.2. Que signifient ces chiffres ?
Le premier est une focale équivalente. Notez que les seconds sont des dénominateurs. Enfin, 49,2 est à peu près égal 12x4,1.
Question 2)
Lorsque la focale du zoom optique est réglée sur la plus courte distance, 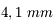 , le compact offre une focale équivalente de
, le compact offre une focale équivalente de 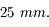 Déduisez-en la taille du capteur.
Déduisez-en la taille du capteur.
Question 3)
Quelle est alors la focale équivalente en position de zoom maximal ?
L'appareil affiche un zoom optique de 12x.
L'oeil
Auteur: Benjamin Mollier
L'oeil
Restons sur un système optique simple, l'oeil. Lui aussi peut être modélisé par une simple lentille placée devant un écran.
L'étude préalable de l'oeil est nécessaire pour aborder les instruments subjectifs. Ce sera l'occasion de nous familiariser avec cet organe.
Mon oeil !
Crédit :
A. Proust
Description
 Description
Description
De façon schématique, l'oeil est de forme sphérique. Il est constitué :
- de l'iris, qui joue le rôle de diaphragme,
- du cristallin, qui est une lentille convergente de distance focale image variable,
- et de la rétine, qui est notre détecteur.
L'oeil
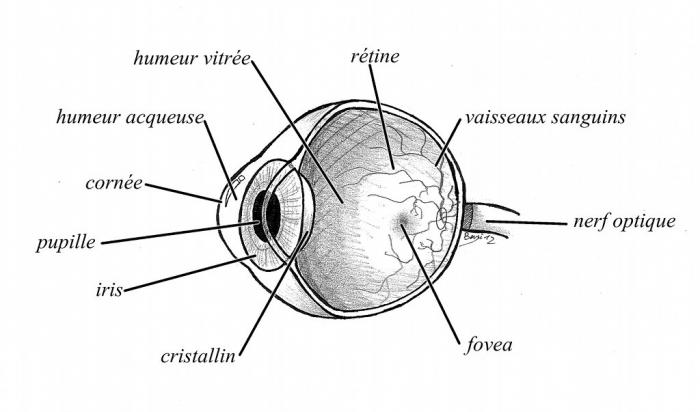
Coupe d'un oeil humain.
Crédit :
B. Mollier
 Modélisation
Modélisation
On le modélisera donc par un diaphragme placé devant une lentille de distance focale variable, le tout devant un écran.
Modèle de l'oeil
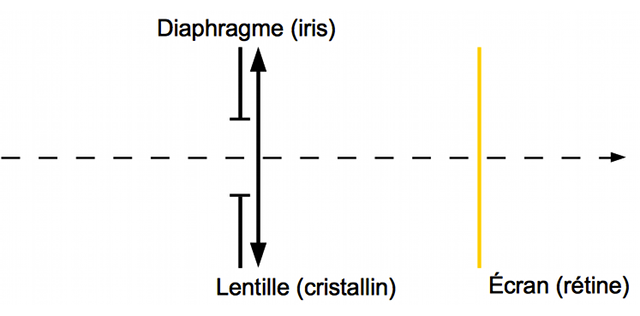
Crédit :
ASM/B. Mollier
Quelques caractéristiques de l'oeil
Auteur: B. Mollier
 Angle de champ d'un oeil
Angle de champ d'un oeil
Difficulté : ☆
Temps : 10 min
Un oeil moyen mesure 2,5 cm de diamètre.
Question 1)
La zone sensible de la rétine s'étend sur environ 2-2,5 cm de diamètre. Donnez approximativement l'angle de champ de l'oeil.
Question 2)
Cependant, la zone permettant la perception des détails fins correspond à une image formée sur la fovéa, une zone très riche en récepteurs, au voisinage de l'axe optique. Cette zone mesure un demi millimètre de diamètre. Donnez l'ordre de grandeur de l'angle de champ correspondant à la fovéa.
 Ouverture de l'oeil
Ouverture de l'oeil
Difficulté : ☆
Temps : 5 min
Le diamètre de l'iris varie, selon la luminosité, de 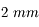 à
à 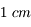 .
.
Question 1)
Calculez les ouvertures minimale et maximale de l'oeil.
Exercice : accomodation
Auteur: B. Mollier
 Distance focale de l'oeil
Distance focale de l'oeil
Un oeil moyen mesure 2,5 cm de diamètre.
Question 1)
Quel doit être la distance focale image du cristallin pour former l'image d'un objet situé à l'infini, sur la rétine ?
Question 2)
Et quelle doit être la valeur de cette distance focale pour lire un livre à 25 cm de l'oeil ?
Question 3)
Que peut-on en conclure ?
Accomodation
 L'accomodation
L'accomodation
Lorsque l'objet se rapproche, son image s'éloigne du cristallin. L'oeil ayant une taille fixe, l'image ne se forme plus sur la rétine. Comment faire alors ? On peut augmenter la vergence du cristallin. Celui-ci, plus convergent, ramène l'image sur la rétine. C'est l'accommodation (voir l'exercice page précédente).
 Punctum proximum
Punctum proximum
Cependant, on ne peut augmenter indéfiniment la vergence. Approchez-vous de l'écran. Au bout d'un moment, vous avez mal aux yeux et n'arrivez plus à voir cet écran net. La distance minimale à laquelle on peut encore voir un objet est appelée punctum proximum, notée 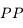 .
.
 Oeil emmétrope
Oeil emmétrope
Pour un oeil normal adulte, dit oeil emmétrope, le punctum remotum est situé à l'infini, et le punctum proximum à 25 cm.
Oeil emmétrope
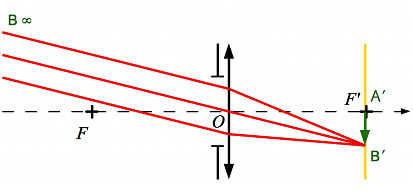
Crédit :
ASM/B. Mollier
Les défauts de vision
L'oeil humain peut être affecté de nombreux défauts de vision.
 La myopie
La myopie
L'oeil myope est trop long ou le cristallin trop convergent. L'image d'un objet à l'infini se forme en avant de la rétine. Le punctum remotum est situé à une distance finie, variant avec la gravité de la myopie.
Myopie
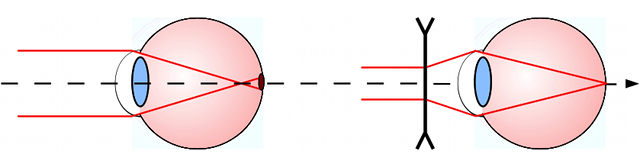
L'oeil myope est trop long ou le cristallin trop convergent. L'image se forme en avant de la rétine (à gauche). L'ajout d'une lentille divergente éloigne l'image qui se forme alors sur la rétine (à droite).
Crédit :
ASM/B. Mollier
Le 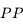 est également plus proche. Un myope peut lire de plus près et est un peu moins sensible à la presbytie.
est également plus proche. Un myope peut lire de plus près et est un peu moins sensible à la presbytie.
Pour corriger ce défaut, il faut donc diminuer la vergence de l'oeil en plaçant devant une lentille divergente.
 L'hypermétropie
L'hypermétropie
À l'inverse, un oeil hypermétrope est trop court ou le cristallin n'est pas assez convergent. L'image d'un objet à l'infini se forme en arrière de la rétine. L'oeil doit constamment accommoder pour ramener l'image au niveau de la rétine, ce qui provoque une fatigue.
Hypermétropie
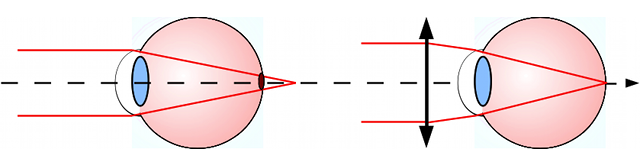
L'oeil hypermétrope est trop court ou le cristallin pas assez convergent. L'image se forme derrière la rétine (à gauche). L'ajout d'une lentille convergente rapproche l'image, qui se forme à nouveau sur la rétine (à droite).
Crédit :
ASM/B. Mollier
Le  est situé derrière l'oeil ! Si si ! On plaisante à ce sujet en disant qu'un hypermétrope peut voir derrière lui. Vous l'aurez compris, le
est situé derrière l'oeil ! Si si ! On plaisante à ce sujet en disant qu'un hypermétrope peut voir derrière lui. Vous l'aurez compris, le  se situe dans l'espace image. C'est-à-dire qu'il est possible, pour un oeil hypermétrope de former l'image d'objets virtuels.
se situe dans l'espace image. C'est-à-dire qu'il est possible, pour un oeil hypermétrope de former l'image d'objets virtuels.
Le 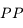 est plus éloigné que la normale.
est plus éloigné que la normale.
Domaine de vision nette
En haut l'oeil emmétrope. Le
est à l'infini et le
à environ
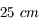
. Au milieu l'oeil myope. Le
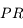
n'est plus à l'infini : on voit mal de loin. Le
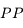
s'est rapproché de l'oeil. Un myope peut lire de plus près. En bas, un oeil hypermétrope. le
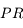
est passé dans l'espace objet virtuel, il est situé derrière le cristallin. Le
s'est éloigné : on voit mal de près.
Crédit :
ASM/B. Mollier
La correction est alors nécessaire pour voir de près, et pour diminuer la fatigue quand on regarde loin. Comme il faut augmenter la vergence du cristallin, on utilise des lentilles convergentes.
 La presbytie
La presbytie
La presbytie se rapproche de l'hypermétropie, mais à une cause toute autre. Elle est liée au vieillissement de l'oeil qui ne parvient plus à accommoder correctement. La vergence du cristallin n'augmente plus et il devient impossible de voir de près. Par contre, la vision de loin reste inchangée. Le  reste à l'infini alors que le
reste à l'infini alors que le  s'éloigne progressivement.
s'éloigne progressivement.
Il faut donc corriger la vision de près à l'aide de verres convergents, mais les retirer pour regarder au loin. On peut utiliser des verres dits progressifs, qui sont des verres dont la vergence augmente vers le bas de la lentille.
 Astigmatisme
Astigmatisme
Comme son nom l'indique, pour un oeil astigmate, la condition de stigmatisme n'est plus respectée.
L'oeil ne possède pas une symétrie de révolution. Il faut utiliser des lentilles non sphériques pour corriger ce défaut.
Exercice : correction de la myopie
Auteur: B. Mollier
 Correction de la myopie
Correction de la myopie
Difficulté : ☆☆
Temps : 20 min
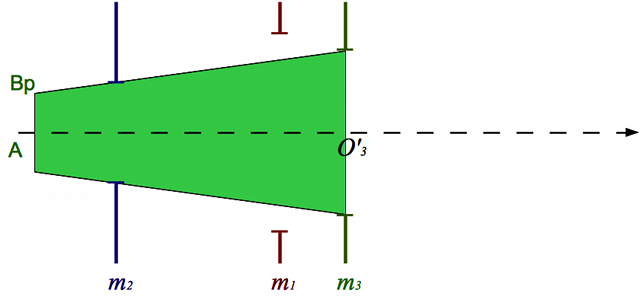
Nous allons chercher à corriger un défaut de myopie à l'aide d'une paire de lunettes. On place une lentille divergente (en bleu) devant l'oeil myope (en noir), dont la rétine (en jaune) est trop loin. On considère un point B situé à l'infini.
Correction de l'oeil myope
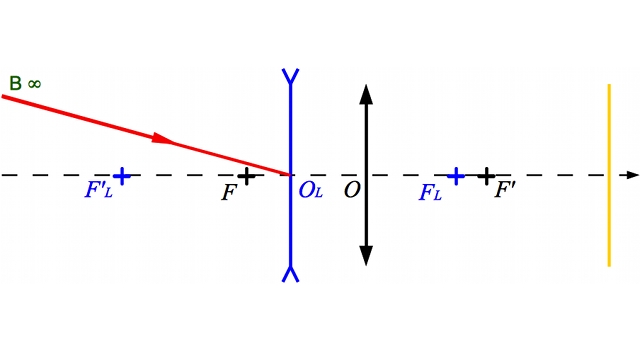
Schéma-énoncé du problème. Le but sera de tracer l'image du point B situé à l'infini à travers les lunettes et l'oeil.
Crédit :
ASM/B. Mollier
Question 1)
En imprimant ou recopiant le schéma ci-dessus, tracer l'image de l'objet 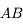 situé à l'infini à travers l'oeil seul. On ne s'occupera pas, dans cette question, de la lentille divergente en bleue. Cette image est-elle située sur la rétine ?
situé à l'infini à travers l'oeil seul. On ne s'occupera pas, dans cette question, de la lentille divergente en bleue. Cette image est-elle située sur la rétine ?
Question 3)
Tracer maintenant l'image 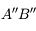 de l'objet
de l'objet 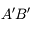 à travers la lentille convergente. Où est située cette image ? Est-elle réelle ? virtuelle ? droite ? inversée ?
à travers la lentille convergente. Où est située cette image ? Est-elle réelle ? virtuelle ? droite ? inversée ?
Associations de lentilles (1)
 Et si on utilisait plusieurs lentilles ?
Et si on utilisait plusieurs lentilles ?
Nous avons uniquement considéré, jusqu'à présent, des systèmes optiques simples, ne comportant qu'une seule lentille. Certes, on peut déjà réaliser un certain nombre de dispositifs optiques : loupe, paire de lunettes, oeil. On est cependant vite limité.
Si on veut pouvoir augmenter la convergence d'un dispositif, en améliorer sa qualité d'image en corrigeant les aberrations, on est amené à associer plusieurs lentilles.
Dans l'exercice précédent, par exemple, on a utilisé une deuxième lentille pour corriger un défaut de vision.
 Type de doublet
Type de doublet
En utilisant deux lentilles, ce qu'on appellera un doublet, nous allons distinguer deux cas, même si le premier se révélera un cas particulier du second.
- Les lentilles peuvent être accolées.
- Les lentilles sont distantes.
 Construction géométrique
Construction géométrique
Pour la construction géométrique, et pour les calculs également, la méthodologie est simple. Nous venons de la voir dans l'exercice précédent.
- Dans un premier temps, on s'intéresse uniquement à la première lentille, sans se préoccuper de la seconde. On recherche alors l'image qu'elle délivre de notre objet.
- Dans un second temps, on oublie la première lentille. L'image précédente devient un objet, réel ou virtuel, selon les cas, pour la seconde lentille. Il reste plus qu'à déterminer son image à travers cette dernière.
Associations de lentilles (2)
 Démonstration
Démonstration
Pour vous en convaincre, voici la démonstration. Si on applique la relation de conjugaison de Descartes aux deux lentilles  et
et 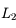 , on obtient :
, on obtient :
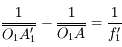 et
et 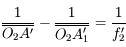
Et on en tire donc :
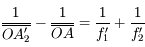
Remarques :
- Si la somme des vergences est non nulle, on vient de le voir, nos deux lentilles sont équivalentes à une seule lentille dont la vergence est la somme des deux autres.
- Si la somme des vergences est nulle, nos lentilles sont équivalentes à une simple lame de verre. Le grandissement vaut 1. Le système n'a pas de foyer.
Exercice bilan : correction de l'hypermétropie
Auteur: B. Mollier
 Correction de l'hypermétropie
Correction de l'hypermétropie
Difficulté : ☆☆
Temps : 20 min
Après la myopie, l'hypermétropie. Nous allons tenter de déterminer la vergence d'une lentille de contact correctrice pour l'hypermétropie.
Question 1)
On considère un oeil hypermétrope de distance focale image variant entre 2,27 cm et 2;5 cm. Sa profondeur est de 2,3cm
On place un objet (un livre par exemple) à 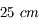 de l'oeil. Où se situe son image ? Est-elle sur la rétine ?
de l'oeil. Où se situe son image ? Est-elle sur la rétine ?
L'objet étant à distance fini, l'oeil accommode.
Question 2)
Quelle devrait être la distance focale pour que l'image se forme sur la rétine ?
Question 3)
On souhaite corriger cette hypermétropie par des lentilles de contact. Comme leur nom l'indique, elles sont au contact de l'oeil. On pourra donc considérer le système lentille de contact + cristallin comme un doublet de deux lentilles accolées. Calculer la vergence de la lentille de contact permettant de former l'image du livre sur la rétine. Quelle est la nature de cette lentille ?
Reprenez la distance focale calculée à la question précédente.
Résumé
 Modélisation
Modélisation
L'oeil, comme l'appareil photo, peut être modélisé par une lentille (le cristallin) placée devant un écran (la rétine). La vergence de cette lentille est variable. L'iris joue le rôle d'un diaphragme.
 Défauts de vision
Défauts de vision
L'oeil peut être affecté de nombreux défauts de vision dont les principaux sont la myopie (l'image d'un objet à l'infini se forme en avant de la rétine), l'hypermétropie (l'image d'un objet proche se forme derrière la rétine), la presbytie (l'oeil n'accommode plus assez) et l'astigmatisme (l'oeil perd sa symétrie de révolution).
 Lentilles accolées
Lentilles accolées
Deux lentilles accolées sont équivalentes à une seule lentille dont la vergence résultante est la somme des deux vergences de chacune des lentilles.
La loupe et l'oculaire
Auteur: Benjamin Mollier
L'oeil et la loupe
Nous allons étudier, dans cette section, le système optique oeil + loupe. C'est, vous l'aurez reconnu, un doublet de deux lentilles convergentes.
Pourquoi étudier le système oeil + loupe ? Parce que tous les instruments d'optique subjectifs possèdent un oculaire, qui est équivalent à une loupe. Étudier ce système nous permettra de nous familiariser avec les notions de grossissement, de puissance, de netteté de l'image...
L'intérêt d'une loupe, d'un oculaire
 Intérêt de la loupe
Intérêt de la loupe
Pour observer les détails d'un objet, il est nécessaire de le rapprocher le plus possible de notre oeil, au 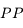 . Cependant, cela entraîne une fatigue de l'oeil, et, avec l'âge, ce point s'éloigne.
. Cependant, cela entraîne une fatigue de l'oeil, et, avec l'âge, ce point s'éloigne.
Utiliser une lentille convergente, une loupe, va nous permettre d'obtenir une image de taille angulaire plus grande que l'objet. On grossit l'image !
De plus, en plaçant l'objet au foyer de la loupe, l'image est à l'infini. L'oeil n'a pas besoin d'accommoder et ne se fatigue plus.
 Intérêt de l'oculaire
Intérêt de l'oculaire
L'oculaire, qui est une sorte de loupe, permet de rendre subjectif l'objectif d'une lunette ou d'un télescope. Il renvoie l'image issue de ces derniers à l'infini, afin d'être vue par l'oeil, sans se fatiguer.
En fonction de leur focale, les oculaires permettent d'agrandir l'image de l'objet et de réduire ou d'augmenter l'angle de champ.
Rappel sur l'angle apparent
 Angle apparent
Angle apparent
L'oeil est sensible à l'angle apparent d'un objet. En effet, il ne fait pas la distinction entre un objet proche et petit et un objet grand et lointain. Certes, le cerveau y arrive en interprétant diverses informations, comme la vision en 3 dimensions, ainsi que le paysage dans son ensemble, mais fermez un oeil, vous verrez que c'est tout de suite moins évident.
L'autre exemple est celui de la Lune et du Soleil, qui n'ont pas la même taille, mais qui ont le même diamètre apparent.
Le but d'une loupe, d'un oculaire, puis des systèmes comme les lunettes et les télescopes, est d'augmenter l'angle apparent.
 Angle apparent d'un objet à l'infini
Angle apparent d'un objet à l'infini
Pour un objet à l'infini, l'angle apparent est directement l'angle sous lequel on voit l'objet. Pour mémoire, le diamètre apparent de la Lune et du Soleil est de 0,5°.
 Angle apparent d'un objet proche
Angle apparent d'un objet proche
S'il est proche, ce diamètre est donné par le rapport de sa taille par sa distance à l'oeil.
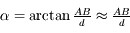
 Remarque
Remarque
Pour un objet proche, l'angle apparent dépend bien sûr de la distance à laquelle il se trouve.
Exercice : angle apparent
 Tour Eiffel
Tour Eiffel
Question 1)
Quel est l'angle apparent de la tour Eiffel vue depuis l'esplanade du Trocadéro ?
La tour Eiffel mesure 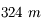 et est distante de
et est distante de 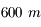 de l'esplanade.
de l'esplanade.
Question 2)
Sur l'esplanade, de nombreux vendeurs à la sauvette peuvent vous proposer des tours Eiffel miniatures. À quelle distance doit-on se situer d'une petite tour Eiffel de 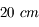 pour obtenir le même angle apparent ?
pour obtenir le même angle apparent ?
L'image d'un objet à travers une loupe
 Utiliser une loupe
Utiliser une loupe
Je rappelle qu'une loupe est une lentille convergente. Pour fonctionner en "loupe", il faut placer l'objet entre le foyer principal objet et la lentille.
 Construction de l'image
Construction de l'image
Construisons l'image d'un objet à travers une loupe.
Image à travers une loupe
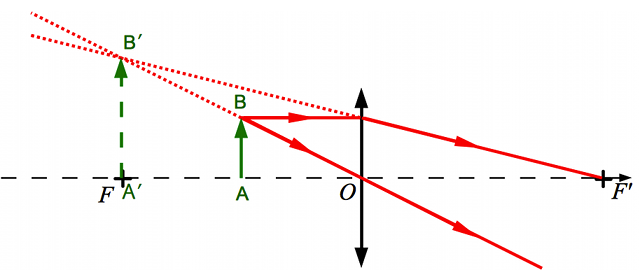
Crédit :
ASM/B. Mollier
 Angle apparent de l'image
Angle apparent de l'image
L'image est plus grosse et plus éloignée. Quel est alors son angle apparent ?
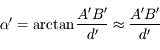
Cet angle dépend de la distance entre la loupe et l'objet, ainsi que de la loupe et l'oeil.
 Cas limite : l'objet est au foyer
Cas limite : l'objet est au foyer
Plaçons nous plutôt dans le cas le plus reposant pour l'oeil (ainsi que le plus simple mathématiquement) : l'image rejetée à l'infini. Pour cela, il suffit de placer le foyer principal objet sur l'objet qu'on veut observer.
Objet au foyer
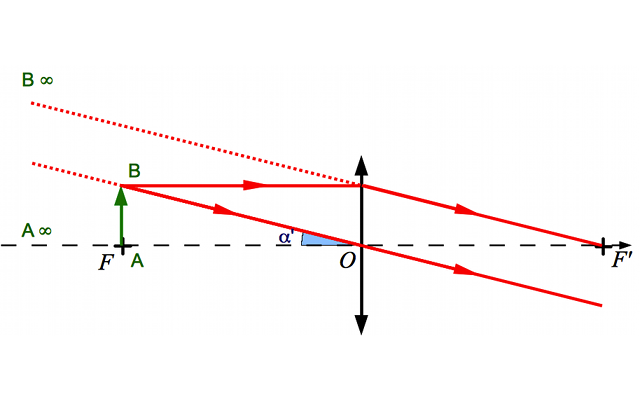
L'objet est placé au foyer, l'image est à l'infini.
Crédit :
ASM/B. Mollier
L'expression de l'angle apparent est alors immédiate
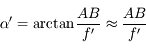
L'angle apparent dépend maintenant de la distance focale de la loupe, et uniquement de celle-ci. Plus cette distance est courte, plus grand sera l'angle apparent. On aimerait dire que, plus la loupe est convergente, plus elle grossit notre image. Mais que veut vraiment dire grossir ?
Le grossissement
 Le grossissement
Le grossissement
On a à notre disposition deux diamètres apparents, l'un avec, l'autre sans la loupe (ou l'instrument subjectif en général).
On peut définir naturellement le grossissement  comme étant le rapport de ces deux quantités :
comme étant le rapport de ces deux quantités :
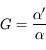
Plus un instrument est grossissant (c'est-à-dire plus 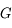 est grand) plus grand sera le diamètre apparent de l'image.
est grand) plus grand sera le diamètre apparent de l'image.
Grossissement d'un objet à l'infini
Le grossissement est le rapport de l'angle apparent de l'image sur l'angle apparent de l'objet.
Crédit :
ASM/B. Mollier
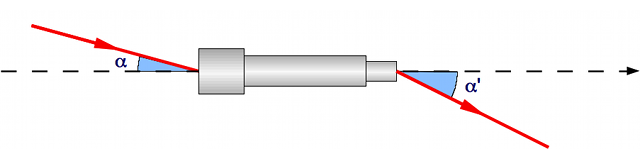
Grossissement d'un objet à distance finie
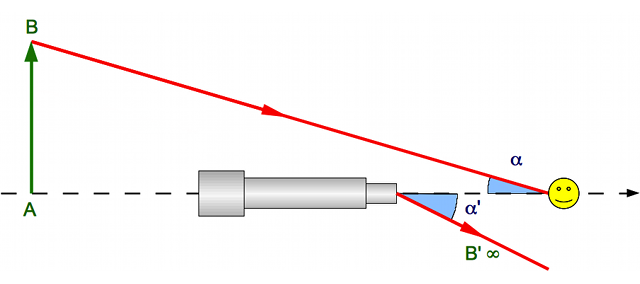
Le grossissement est le rapport de l'angle apparent de l'image sur l'angle apparent de l'objet.
Crédit :
ASM/B. Mollier
 Attention
Attention
Ne pas confondre grossissement et grandissement !
Le grossissement commercial
 Position du problème
Position du problème
Petit problème : pour un objet à distance 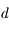 finie, le diamètre apparent
finie, le diamètre apparent 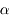 dépend de la position de l'oeil. Or il serait bon d'avoir un grossissement ne dépendant que de l'instrument. Cela nous permettra de les comparer entre eux.
dépend de la position de l'oeil. Or il serait bon d'avoir un grossissement ne dépendant que de l'instrument. Cela nous permettra de les comparer entre eux.
Le microscope ou la loupe sont des exemples de système optique grossissant des objets à distance finie.
La puissance
 La puissance
La puissance
On définit également, pour le cas des objets à distance finie, la puissance de l'instrument, comme étant le rapport de diamètre apparent de l'image, sur la taille 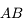 de l'objet :
de l'objet :
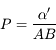
 Remarques
Remarques
Remarquons que 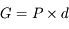
En astronomie, la distance  tend vers l'infini. La puissance est donc toujours nulle.
tend vers l'infini. La puissance est donc toujours nulle.
Si l'image est à l'infini, donc l'objet au foyer principal objet, la puissance est simplement la vergence de l'instrument : 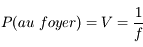
Latitude de mise au point
L'oculaire
De nombreux instruments sont équipés d'oculaires : télescopes, lunettes, microscopes...
Cet instrument comprend plusieurs lentilles, mais joue le rôle d'une loupe. Il est cependant plus puissant, corrige les aberrations optiques et chromatiques, possède un champ plus grand. Il peut parfois être équipé d'un réticule pour mesurer des tailles angulaires, des parallaxes ou viser...
Résumé
 La loupe
La loupe
Une loupe est une lentille convergente. Elle sert à grossir les objets. Une utilisation optimale consiste à placer son foyer sur l'objet visé. Son image est alors rejetée à l'infini. L'oeil n'a pas besoin d'accommoder et se fatigue moins.
 Le grossissement
Le grossissement
Le grossissement est le rapport de l'angle apparent de l'image sur celui de l'objet :
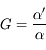
 La puissance
La puissance
On a également défini la puissance 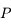 comme étant le rapport entre la taille de l'objet et le diamètre apparent de l'image.
comme étant le rapport entre la taille de l'objet et le diamètre apparent de l'image.
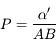
La lunette astronomique
Auteur: Benjamin Mollier
La lunette astronomique
Il est désormais temps de l'utiliser, ce fameux oculaire. Commençons par le mettre à la sortie d'une lunette astronomique.
Description de la lunette astronomique
 La lunette astronomique
La lunette astronomique
Une lunette astronomique est constituée de deux lentilles :
- Une lentille objectif, en entrée de l'instrument, qui capte la lumière de l'astre et en fait l'image à son foyer.
- Une lentille oculaire, en sortie, qui, nous l'avons déjà vu, rejette l'image de l'astre à l'infini afin d'en faciliter son observation à l'oeil.
Dans le cas d'une lunette astronomique, les deux lentilles sont convergentes, et l'image de l'astre sera inversée.
La lunette astronomique
Une lunette est constituée de deux lentilles convergentes en entrée (objectif) et sortie (oculaire).
Crédit :
B. Mollier
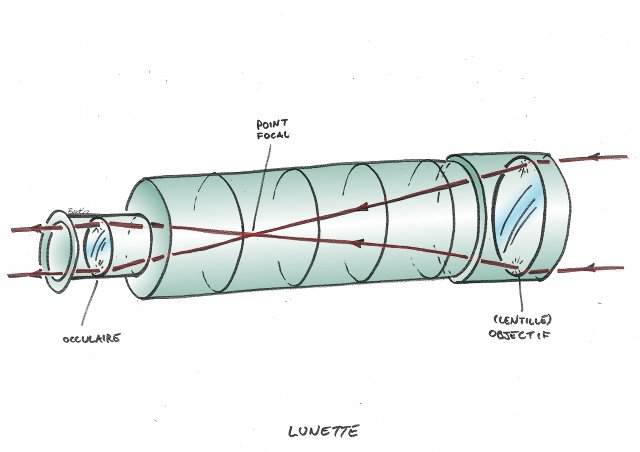
 La lunette de Galilée
La lunette de Galilée
La lunette de Galilée se distingue par la nature de la lentille oculaire. Cette dernière est ici divergente. L'image en sortie sera droite.
À focale équivalente, la lunette de Galilée sera plus courte. Nous verrons pourquoi.
Lunette astronomique - Lunette de Galilée
En haut, une lunette astronomique avec 2 lentilles convergentes. En bas, une lunette de Galilée avec un objectif convergent et un oculaire divergent.
Crédit :
ASM/B. Mollier
Principe de fonctionnement
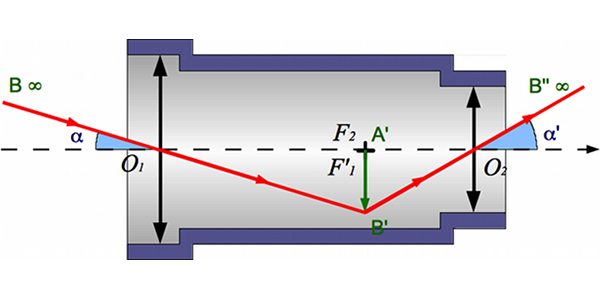
 L'objectif
L'objectif
L'objectif capte la lumière provenant de l'astre, et en fait l'image 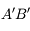 à son foyer.
à son foyer.
Plus la focale de l'objectif sera grande, plus l'image sera également grande. Et si on se rappelle de la section sur l'appareil photo, on se souviendra que son angle de champ sera d'autant plus petit que cette focale est grande.
Principe de fonctionnement
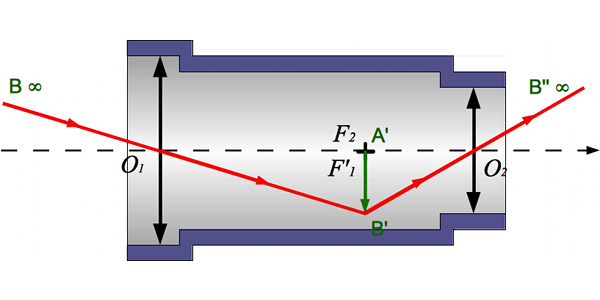
Crédit :
ASM/B. Mollier
 L'oculaire
L'oculaire
L'image intermédiaire 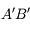 étant en général petite, il faut la regarder avec une loupe : l'oculaire. Ce dernier grossit l'image et la rejette à l'infini.
étant en général petite, il faut la regarder avec une loupe : l'oculaire. Ce dernier grossit l'image et la rejette à l'infini.
Et si on fait appel au cours sur la loupe, on se souviendra que l'image finale 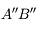 est d'autant plus grande que la focale de l'oculaire est courte.
est d'autant plus grande que la focale de l'oculaire est courte.
 Remarques
Remarques
- Compte-tenu de ce qu'on vient de dire, on sent bien que l'image de notre astre sera d'autant plus grosse que la focale de l'objectif est longue et celle de l'oculaire est courte. Le grossissement serait-il égal au rapport des deux focales ? La réponse page suivante.
- Le principe de fonctionnement est le même pour la lunette de Galilée. La seule différence étant que l'image intermédiaire
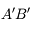 constitue un objet virtuel pour l'oculaire.
constitue un objet virtuel pour l'oculaire.
 Système afocal
Système afocal
Dans une lunette (et, nous le verrons également, un télescope) l'objet est à l'infini et l'image aussi. Ce système n'a donc pas de foyer. Il est dit afocal.
Comment réaliser un tel système ? L'image intermédiaire est, par définition, au foyer principal image de l'objectif. Pour projeter l'image finale 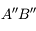 à l'infini, nous avons placé le foyer principal objet sur l'image intermédiaire.
à l'infini, nous avons placé le foyer principal objet sur l'image intermédiaire.
Bref, pour fabriquer un système afocal, il suffit de superposer le foyer principal image de l'objectif avec le foyer principal objet de l'oculaire.
Grossissement
Nous allons calculer le grossissement d'une lunette astronomique en fonction des focales de son objectif et de son oculaire. Nous vérifierons ainsi si l'hypothèse émise à la page précédente est juste.
 Calcul du grossissement
Calcul du grossissement
Par définition de grossissement 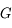
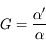
Il vient assez immédiatement que
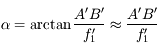 et
et 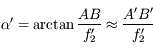
D'où 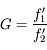
 Remarques
Remarques
L'image sera d'autant plus grande que la focale de l'objectif sera grande et celle de l'oculaire petite. On trouve bien le résultat qui était attendu.
Ce résultat est valable également pour la lunette de Galilée.
Grossissement
Le grossissement d'une lunette est égale au rapport des focales de l'objectif et de l'oculaire.
Crédit :
ASM/B. Mollier
Exercice : grossissement
Auteur: B. Mollier
 Observation de Jupiter
Observation de Jupiter
Difficulté : ☆☆
Temps : 20 min
On souhaite observer Jupiter à l'aide d'une lunette de 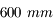 de focale (il s'agit ici de la focale de l'objectif).
de focale (il s'agit ici de la focale de l'objectif).
Jupiter

Jupiter, photographiée au télescope de
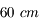
de la table équatoriale, à l'observatoire de Meudon. On y voit la grande tache rouge (bande rouge du haut), ainsi qu'une tempête (bande rouge du bas).
Crédit :
P. Kervella
Question 1)
Calculer le diamètre apparent de cette planète à l'opposition.
On parle d'opposition quand la planète est au plus proche de la Terre.
Le rayon équatorial de Jupiter est de 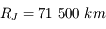 . À l'opposition, elle se situe à environ
. À l'opposition, elle se situe à environ 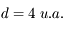 de la Terre.
de la Terre.
Question 2)
Vous disposez de 3 oculaires de 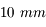 ,
, 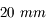 et
et 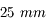 de focale respectivement. Lequel devez-vous utiliser pour obtenir le meilleur grossissement ?
de focale respectivement. Lequel devez-vous utiliser pour obtenir le meilleur grossissement ?
Question 3)
Calculez alors le diamètre apparent de Jupiter dans cet oculaire.
Question 4)
La grande tache rouge mesure à peu près 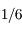 du diamètre de Jupiter. Sera-t-elle visible dans cet instrument ?
du diamètre de Jupiter. Sera-t-elle visible dans cet instrument ?
La résolution de l'oeil, c'est-à-dire la taille du plus petit détail visible, est de l'ordre de 1'.
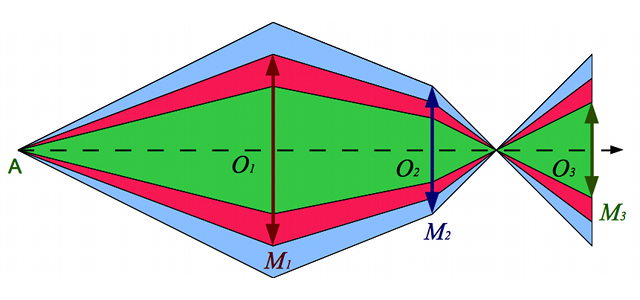
Champ d'une lunette astronomique
Ce qui va suivre ne s'applique pas aux lunettes de Galilée.
 Champ d'une lunette astronomique
Champ d'une lunette astronomique
Le champ de la lunette est l'ensemble des points de l'espace visibles dans l'instrument. Comme dans le cas de l'appareil photo, cet espace est un cône. Les objets à l'intérieur de celui-ci seront visibles, ceux à l'extérieur, non.
Grand champ

La grande coupole de l'observatoire de Meudon. Le champ de vue est grand ici.
Crédit :
B. Mollier
Champ réduit

La grande coupole de l'observatoire de Meudon. Le champ de vue est réduit.
Crédit :
B. Mollier
 Champ de l'oculaire
Champ de l'oculaire
L'image en sortie sera-t-elle petite ? (c'est-à-dire qu'on pourra l'embrasser en entier sans bouger l'oeil), ou au contraire sera-t-elle grande ? (il faudra alors bouger son oeil pour tout voir, ce qui n'est pas forcément agréable). C'est ce qu'on appellera le champ de l'oculaire.
Pour l'instant, nous ferons l'hypothèse que le champ de l'oculaire est celui de l'oeil, c'est-à-dire 50°.
Champ de l'oculaire réduit

Lorsque le champ de l'oculaire est réduit (inférieur à 50°), on peut voir toute l'image sans bouger l'oeil.
Crédit :
B. Mollier
Champ de l'oculaire grand

Lorsque le champ de l'oculaire est trop grand (supérieur à 50°) comme ici, on ne peut pas voir toute l'image sans bouger l'oeil. C'est fatiguant et peu agréable. (Cliquez sur l'image pour agrandir)
Crédit :
B. Mollier
 Remarques
Remarques
Le champ est inversement proportionnel au grossissement. Pour une lunette donnée, et donc une focale fixée, le champ diminue avec la focale de l'oculaire. Plus l'oculaire est court, plus le champ est réduit.
La démonstration de ce résultat est ici.
Champ d'une lunette astronomique, démonstration
Le champ d'une lunette est limité par le diaphragme de champ
Champ d'une lunette
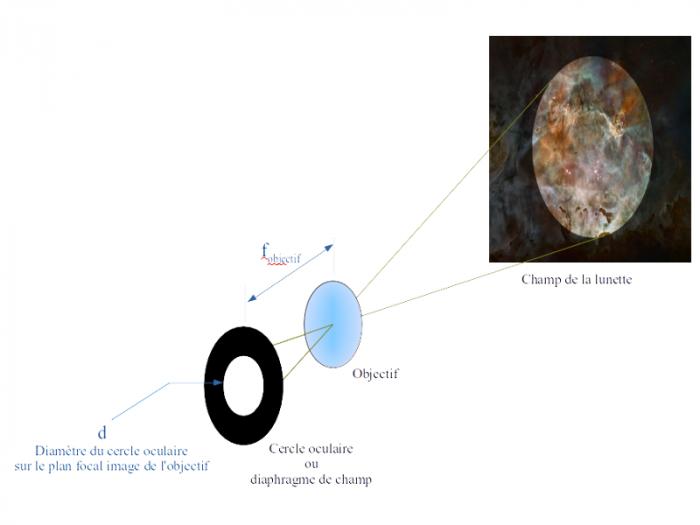
L'expression du champ d'une lunette est très proche de celle d'un appareil photographique : où d est le diamètre du diaphragme de champ, au niveau du plan focal image de l'objectif, f_objectif la distance focale image de l'objectif.
La démonstration de ce résultat est très simple, puisqu'il suffit d'écrire la définition de la tangente de l'angle
Observer la Lune
Auteur: B. Mollier
 Observation de la Lune
Observation de la Lune
Par une nuit de pleine Lune, on désire observer l'astre sélène. On possède une lunette de 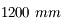 de focale, ainsi qu'un oculaire de
de focale, ainsi qu'un oculaire de 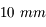 de focale et de
de focale et de 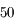 ° de champ.
° de champ.
Question 1)
Calculez le grossissement de cet instrument.
Question 2)
À partir du champ de l'oculaire, calculez l'angle de champ de la lunette. Pourra-t-on voir la Lune en entier dans l'oculaire ? Et la Galaxie d'Andromède (M31) ?
Le diamètre apparent de la Lune est de 0,5°. Celui de M31 est de  .
.
Diaphragme d'ouverture - Pupilles
Dans les quelques pages à venir, nous allons rentrer dans des détails un peu plus techniques. Je les donne pour satisfaire la curiosité du lecteur, mais ils ne rentreront pas aux programmes de l'examen.
 Diaphragme d'ouverture
Diaphragme d'ouverture
Considérons un instrument possédant un certain nombre de lentilles. Faisons avec l'image d'un point  situé sur l'axe optique.
situé sur l'axe optique.
Diaphragme d'ouverture
La lentille
est celle qui limite le plus la taille du faisceau. Le faisceau rouge, prenant appui sur la monture
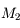
est vignété par
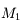
. Le faisceau bleu, prenant appui sur la monture
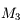
est vignété par
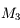
et
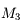
. La lentille
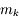
joue le rôle de diaphragme d'ouverture.
Crédit :
ASM/B. Mollier
Ce point émet un faisceau lumineux. Certains rayons de ce faisceau ressortiront de l'instrument, d'autres seront interceptés par la monture d'une des lentilles.
Pour connaître la quantité de lumière qui ressort de l'instrument, il faut chercher la monture qui limite la taille du faisceau (sur notre image, c'est la monture 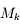 ).
).
On nommera cette monture diaphragme d'ouverture.
 Exemples de diaphragme d'ouverture
Exemples de diaphragme d'ouverture
Sur une lunette et un télescope, où on cherche à avoir le plus de lumière, on construit l'instrument de telle sorte que le diaphragme d'ouverture soit la première lentille (ou le miroir primaire). Comme c'est l'optique la plus grande, il serait dommage qu'elle ne serve à rien si c'est une autre monture plus petite qui joue le rôle de diaphragme d'ouverture.
En photographie, la problématique est différente. L'ouverture étant liée au temps de pose et à la profondeur de champ, on cherche à la contrôler en fonction de l'effet recherché. C'est donc un diaphragme physique, avec un diamètre ajustable, placé dans l'objectif, qui servira de diaphragme d'ouverture.
 Pupille d'entrée, pupille de sortie
Pupille d'entrée, pupille de sortie
Pour rechercher quelle monture limite la largeur de notre faisceau, une méthode consiste à rechercher l'antécédent de ces montures par rapport à toutes les précédentes.
Un rayon qui passera chacun des conjugués 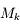 traversera toutes les montures réelles
traversera toutes les montures réelles  . Trouver le diaphragme d'ouverture
. Trouver le diaphragme d'ouverture  revient à chercher le conjugué
revient à chercher le conjugué  dont le diamètre est le plus petit.
dont le diamètre est le plus petit.
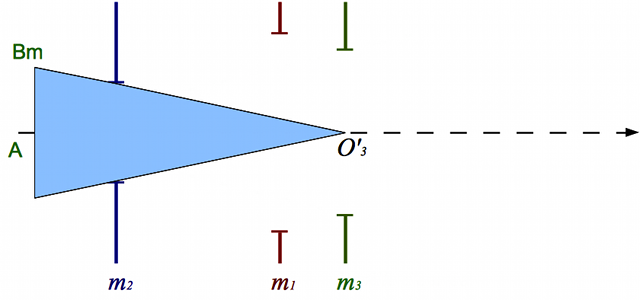
Pupille d'entrée
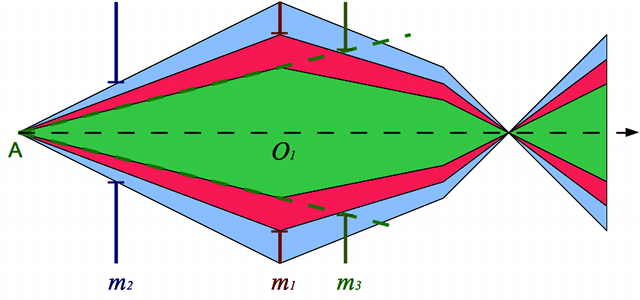
On cherche les antécédents des montures
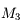
à travers
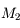
et
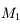
à travers
et
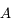
.
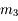
est son propre antécédent. On cherche ensuite lequel de ces antécédents limite le plus le faisceau issu de
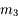
. Ici, c'est
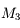
.
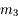
est appelé pupille d'entrée, et son image
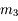
est appelée diaphragme d'ouverture.
Crédit :
ASM/B. Mollier
Ici, c'est 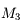 .
.  est appelé pupille d'entrée et
est appelé pupille d'entrée et  diaphragme d'ouverture.
diaphragme d'ouverture.
 Remarque
Remarque
La pupille d'entrée est le conjugué du diaphragme d'ouverture dans l'espace objet.
De la même manière, on définit la pupille de sortie comme étant le conjugué du diaphragme d'ouverture dans l'espace image.
Pour profiter pleinement d'un instrument, il faut que la pupille de sortie et la pupille de l'oeil soient confondues.
Ce n'est pas nécessairement une lentille qui joue le rôle de diaphragme d'ouverture. Ça peut-être un vrai diaphragme, comme dans le cas de l'appareil photo.
On peut également placer un vrai diaphragme physique, en entrée, pour jouer le rôle à la fois de diaphragme d'ouverture et de pupille d'entrée. (En effet, s'il est placé en amont de la première lentille, il est son propre antécédent).
Diaphragme de champ - Lucarne
 Dans ce pragraphe...
Dans ce pragraphe...
... je m'étendrai un peu plus sur la notion de champ d'une lunette, et j'introduirai les notions de diaphragme de champ et de lucarne.
 Diaphragme de champ
Diaphragme de champ
On considère cette fois-ci un point  , hors de l'axe optique. Intéressons-nous au rayon issu de
, hors de l'axe optique. Intéressons-nous au rayon issu de  et passant par le centre de la pupille d'entrée et donc au centre du diaphragme d'ouverture et de la pupille de sortie. Il est appelé rayon moyen ou rayon principal.
et passant par le centre de la pupille d'entrée et donc au centre du diaphragme d'ouverture et de la pupille de sortie. Il est appelé rayon moyen ou rayon principal.
Diaphragme de champ
L'antécédent
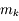
, appelé lucarne d'entrée, est celui qui limite le plus l'angle de champ.
Crédit :
ASM/B. Mollier
Faisons bouger 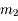 jusqu'à ce que le rayon rayon principal soit intercepté par un des conjugués
jusqu'à ce que le rayon rayon principal soit intercepté par un des conjugués 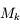 (ici
(ici 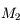 ).
).
Par définition, ce conjugué est appelé lucarne d'entrée, et son antécédent associé 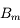 (ici
(ici 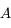 ) est appelé diaphragme de champ.
) est appelé diaphragme de champ.
 Champ moyen
Champ moyen
Le rayon touchant le bord du diaphragme de champ est noté 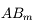 . Il délimite le champ moyen de l'instrument. Le champ moyen est le disque de centre
. Il délimite le champ moyen de l'instrument. Le champ moyen est le disque de centre 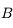 et de rayon
et de rayon 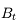 .
.
C'est grosso-modo la portion visible de l'image. (Mais pas tout à fait)
Champ moyen

Le cercle bleu représente le champ moyen. Il délimite à peu près la zone visible.
Crédit :
B. Mollier
Champ de pleine lumière - Champ de contour
Que voit-on réellement dans l'oculaire ?
 Champ de pleine lumière
Champ de pleine lumière
Considérons maintenant un autre du point 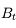 , de telle sorte que le rayon qui en est issu passe par le bord de la lucarne d'entrée et la pupille d'entrée (en vert sur la figure). Il délimite également un champ, plus petit que le précédent appelé champ de pleine lumière.
, de telle sorte que le rayon qui en est issu passe par le bord de la lucarne d'entrée et la pupille d'entrée (en vert sur la figure). Il délimite également un champ, plus petit que le précédent appelé champ de pleine lumière.
Champ pleine lumière
Le faisceau lumineux issu d'un point situé dans le champ pleine lumière passera la pupille d'entrée sans être vignété par la lucarne.
Crédit :
ASM/B. Mollier
Le faisceau lumineux issu d'un point situé dans le champ de pleine lumière passera la pupille d'entrée sans être vignété par la lucarne.
Le faisceau lumineux issu d'un point situé en dehors de ce champ sera en partie, voir totalement, vignété par la lucarne d'entrée. Au delà de ce cercle de pleine lumière, la luminosité commence à décroître.
Champ pleine lumière

Le cercle vert délimite le champ de pleine lumière. Au delà de ce cercle, la luminosité décroît.
Crédit :
B. Mollier
 Champ de contour
Champ de contour
La luminosité décroît jusqu'au cercle de diamètre 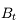 .
.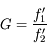 est un point particulier : les rayons qui en sont issus passent par le bord supérieur de la lucarne d'entrée puis par le bord inférieur de la pupille d'entrée. Bref, le faisceau issu de
est un point particulier : les rayons qui en sont issus passent par le bord supérieur de la lucarne d'entrée puis par le bord inférieur de la pupille d'entrée. Bref, le faisceau issu de 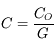 passant par les lucarne et pupille d'entrée se résume à un seul rayon lumineux.
passant par les lucarne et pupille d'entrée se résume à un seul rayon lumineux.
Champ de contour
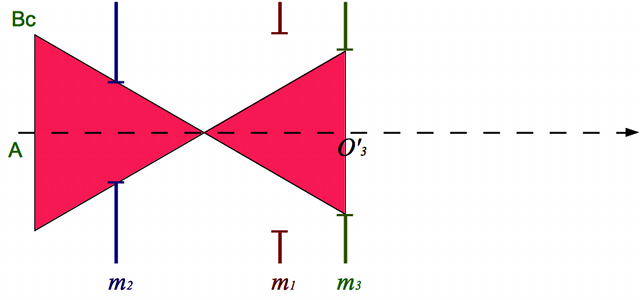
Tout objet situé en dehors de ce champ de contour sera invisible dans la lunette.
Crédit :
ASM/B. Mollier
Il délimite le champ de contour. Ce champ inclut les deux autres champs définis précédemment.
Pur résumer, dans le champ de pleine lumière, toute la lumière rentrant dans la lunette en ressort. En dehors du champ de contour, plus aucune lumière ne ressort de l'instrument. Entre les deux, une partie de la lumière entrante est stoppée quelque part dans la lunette.
Champ de contour

Le cercle rouge représente le champ de contour. Au delà de ce cercle, plus aucune lumière n'est visible.
Crédit :
B. Mollier
Les trois champs

En vert, le champ de pleine lumière, qui est inclus dans le champ moyen (en bleu) qui est inclus dans le champ de contour (en rouge).
Crédit :
B. Mollier
 Ce que l'on voit
Ce que l'on voit
Visuellement, on observe un cercle au bord flou, où la lumière décroît progressivement du centre vers le bord. Ce n'est pas agréable à l'oeil.
Le jeu consiste donc à confondre ces trois champs, afin d'obtenir un bord net. Il faut pour cela déplacer le diaphragme de champ de façon à ce que son conjugué, la lucarne d'entrée, soit dans le même plan que l'objet observé. Dans le cas d'un instrument astronomique, il faut que la lucarne d'entrée soit à l'infini.
Cercle oculaire flou

Ici, le cercle oculaire est flou, ce qui est désagréable à l'oeil. Les trois champs ne sont pas superposés. La lucarne d'entrée n'est pas dans le plan de l'objet (la coupole ici).
Crédit :
B. Mollier
Cercle oculaire net

Ici, le cercle oculaire est net, ce qui est plus agréable à l'oeil. Les trois champs se superposent. La lucarne d'entrée est dans le plan de l'objet (la coupole ici).
Crédit :
B. Mollier
Résumé
 Description d'une lunette
Description d'une lunette
Une lunette est l'association de deux lentilles. Un objectif convergent et un oculaire convergent (lunette astronomique) ou divergent (lunette de Galilée).
 Système afocal
Système afocal
Une lunette est un système afocal, c'est-à-dire que le faisceau issu d'un objet à l'infini ne converge pas en sortie de l'instrument. C'est à l'oeil de faire l'image de cet objet. La lunette est un instrument subjectif.
Pour réaliser un système afocal, il faut superposer le foyer principal image de l'objectif avec le foyer principal objet de l'oculaire.
 Grossissement
Grossissement
Le grossissement d'une lunette est le rapport des focales de l'objectif et de l'oculaire,
Le grossissement sera d'autant plus grand que la focale de la lunette est grande, et celle de l'oculaire réduite.
 Angle de champ
Angle de champ
L'angle de champ de la lunette est proportionnel à celui de l'oculaire (qui est en général de 40-50°) et inversement proportionnel au grossissement :
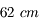
 Diaphragmes
Diaphragmes
Il existe deux types de diaphragmes :
- le diaphragme de champ, qui limite le champ de vue,
- le diaphragme d'ouverture, qui limite l'ouverture, c'est-à-dire la luminosité.
Exercice bilan : la grande lunette de Meudon
Auteur: B. Mollier
 La grande lunette de Meudon
La grande lunette de Meudon
La Grande coupole de l'observatoire de Meudon abrite une des plus grandes lunettes de la planète. Il s'agit en fait de deux lunettes montées en parallèle. L'une mesurant  de diamètre, l'autre
de diamètre, l'autre 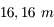 . Elles possèdent toutes deux une focale de
. Elles possèdent toutes deux une focale de 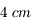 .
.
Grande lunette

La Grande Lunette de l'Observatoire de Meudon. Héliogravure de Dujardin publiée en 1896 dans les Annales de l'Observatoire d'Astronomie Physique de Paris, Sis Parc de Meudon - Volume 1 planche IX.
Crédit :
Observatoire de Paris
Question 1)
La lunette et son oculaire sont réglés de sorte à obtenir un système afocal. La focale de la lunette est de  , celle de l'oculaire est de
, celle de l'oculaire est de 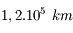 . Calculez le grossissement.
. Calculez le grossissement.
Question 2)
Quel est le diamètre apparent de Saturne, avec et sans ses anneaux, à l'opposition ? Quel sera alors son diamètre dans la lunette ?
Saturne est située à 10 u.a. du Soleil, et possède un diamètre de  . Celui des anneaux est le double.
. Celui des anneaux est le double.
Question 3)
La division de Cassini est-elle visible à la lunette ?
La division de Cassini mesure 5000 km de large.
Question 4)
En supposant que l'angle de champ de l'oculaire est de 50°, calculez l'angle de champ de la lunette. Saturne est-elle visible en entier ?
Question 5)
Calculez l'ouverture de la lunette. Comparez cette valeur à celle des télescopes professionnels modernes.
Les télescopes modernes possèdent des ouvertures de l'ordre de  .
.
Le télescope
Auteur: Benjamin Mollier
Le télescope
Nous allons terminer ce chapitre par l'étude des télescopes.
Le télescope est devenu l'instrument roi de l'astronomie. Nous verrons pourquoi.
Ce dernier chapitre sera assez court, car toutes les notions d'optique ont déjà été abordées. De plus, nous verrons que son étude est très semblable à celui d'une lunette. Il sera d'ailleurs possible de le modéliser par une lunette astronomique.
Une fois terminé ce chapitre, nous quitterons le cadre de l'optique géométrique pour aborder rapidement quelques phénomènes d'origine ondulatoire, comme la diffraction et les interférences.
Les télescopes du VLT

Observatoire de l'ESO sur le mont Paranal, au Chili. Les deux premières coupoles abritent des télescopes de
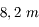
de diamètre !
Crédit :
B. Mollier
Description d'un télescope
S'il existe plusieurs types de télescopes, ils ont tous un point commun : un grand miroir !
 Miroir primaire
Miroir primaire
La pièce essentiel d'un télescope est son miroir primaire. C'est un miroir sphérique (ou parabolique) situé au fond du tube du télescope.
Il joue le rôle de collecteur de lumière. Plus son diamètre est grand, plus il sera lumineux. Un grand miroir a un autre avantage, qui sera exposé au dernier chapitre.
 Miroir secondaire
Miroir secondaire
Un miroir, c'est bien joli, mais comment voir la lumière qui se réfléchit dessus. Bah oui, si je le mets à son foyer, je cache l'entrée du miroir, et donc, pas de lumière.
On doit donc utiliser un second miroir pour "dégager" la lumière du tube. Là, les options sont multiples, et définissent le type de télescope auquel nous avons à faire.
Soit le miroir est un petit plan incliné de 45° par rapport à l'axe optique, et la lumière s'échappera par le côté du tube. C'est un télescope de type Newton. Oui, c'est le télescope qu'avait utilisé Newton en 1671.
Télescope Newton
Le miroir secondaire renvoie la lumière sur le côté du tube. C'est un télescope de type Newton.
Crédit :
B. Mollier
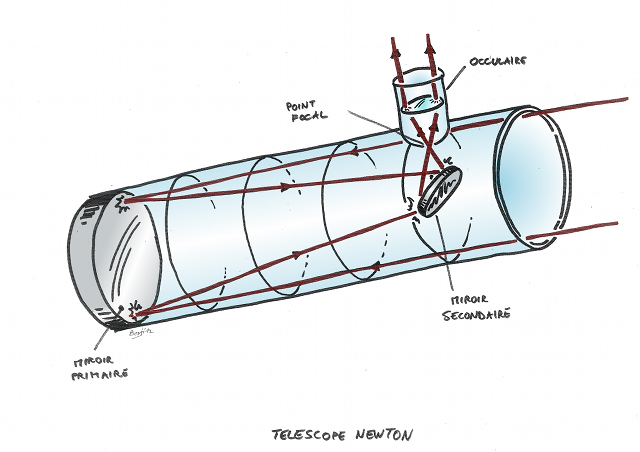
Soit le miroir est un petit miroir plan ou sphérique, perpendiculaire à l'axe optique, renvoyant la lumière vers le fond du tube. Il faut alors percer le miroir primaire pour recueillir cette dernière en sortie de tube. Ce télescope est de type Cassegrain.
Télescope Cassegrain
Le miroir secondaire renvoie la lumière vers le fond du tube. C'est un télescope de type Cassegrain.
Crédit :
B. Mollier
Il en existe d'autres types, combinaison de ces deux télescopes.
 Oculaire
Oculaire
Comme pour une lunette, on a la possibilité de rajouter un oculaire en sortie de télescope pour l'observation à l'oeil.
Miroir primaire

Le miroir primaire du VLT, de
de diamètre tout de même ! Le petit miroir au centre est un miroir tertiaire, qui permet de renvoyer la lumière sur les côtés. Il peut aussi être escamoté pour passer en mode Cassegrain.
Crédit :
B. Mollier
Miroir secondaire

Le miroir secondaire du VLT. Vous reconnaissez ici un miroir convexe.
Crédit :
B. Mollier
Équivalence entre télescope et lunette
Va-t-on être obligé de refaire tout ce qu'on vient de voir sur les lunettes dans les cas des télescopes ? La réponse est heureusement non. En effet, formellement, un télescope et une lunette sont la même chose.
Souvenez-vous qu'un miroir sphérique est en fait une lentille pliée. L'objectif du télescope (le miroir primaire) est donc un objectif de lunette plié.
Équivalence lunette et télescope
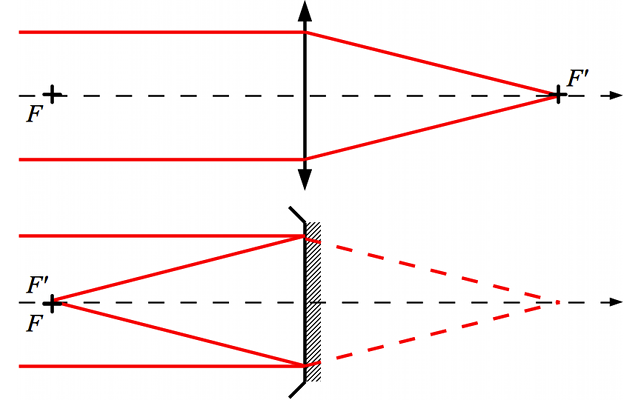
Formellement, un télescope est équivalent à une lunette de même focale.
Crédit :
ASM/B. Mollier
L'ajout d'un miroir secondaire revient à plier une seconde fois notre schéma optique.
Muni de ce résultat, on montre très facilement que, formellement, un télescope est équivalent à une lunette de même focale.
Les résultats concernant le grossissement, le champ de vue, l'ouverture... restent valables pour un télescope.
Grossissement
Les avantages du télescope (1)
Si pendant de nombreuses années, lunettes et télescopes se sont côtoyés dans les observatoires, cela fait bien 50 ans que l'on ne fabrique plus que des télescopes. Pour quelles raisons le monde scientifique a-t-il progressivement abonné la lunette au profit du télescope ? En voici quelques-unes.
 Facilité de la construction
Facilité de la construction
Un grand télescope est plus facile à construire qu'une grande lunette.
Pour capter le plus de lumière possible, il faut que la pupille d'entrée soit la plus grande possible. Pour la lunette, la quantité de lumière reçue est proportionnelle à la surface de la lentille de l'objectif ; pour le télescope, elle est proportionnelle à la surface du miroir primaire.
Pour la lunette, il faut donc construire une grande lentille. Plus elle est grande, plus il est difficile de la garantir sans défaut (aberrations optiques, bulles dans le verre). De plus, étant en verre massif, elle est de plus en plus lourde. Les plus grosses lunettes atteignent péniblement le mètre de diamètre.
Il est plus simple de polir un miroir de grande taille. Pour les petits miroirs, on utilise, comme pour les lunettes, des blocs de verre massif. C'est la même chose, me direz vous. Oui, mais quand leur taille augmente, on utilise des miroirs fins, taillés dans d'autres matériaux et reposant sur une structure rigide ou mobile, donnant au miroir sa forme. Enfin, pour des diamètres supérieurs à 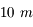 , on segmente le miroir. Il n'est plus monolithique, mais composé de plusieurs pièces hexagonales, assemblées comme un puzzle. Les télescopes actuels mesurent
, on segmente le miroir. Il n'est plus monolithique, mais composé de plusieurs pièces hexagonales, assemblées comme un puzzle. Les télescopes actuels mesurent 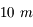 de diamètre. Et on ne s'arrêtera pas là. Des projets de télescopes de
de diamètre. Et on ne s'arrêtera pas là. Des projets de télescopes de 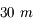 à
à  sont en cours de réalisation.
sont en cours de réalisation.
Les avantages du télescope (2)
 Aberrations chromatiques
Aberrations chromatiques
Si on se souvient du premier chapitre, on a vu que l'indice optique des verres dépendait de la longueur d'onde. Or, une lentille, faite en verre, possède une distance focale dépendant de l'indice optique. Plus l'indice optique est élevé, plus sa vergence augmente. Sa distance focale dépend donc de la longueur d'onde. Les rayons rouges, verts et bleus ne convergeront donc pas au même endroit. Une lunette présente donc des aberrations chromatiques.
Abbérations chromatiques
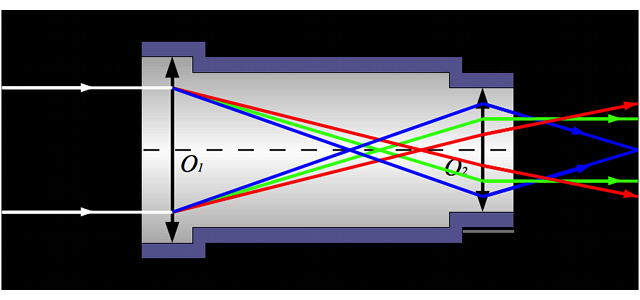
Le verre est un milieu dispersif. Par conséquent, la vergence d'une lentille dépend de la longueur d'onde. Les rayons rouge, vert et bleu ne sont alors plus déviés de la même manière et ne convergent plus au même foyer. On obtient en sortie la superposition d'image de tailles et de couleurs différentes. Ce sont des aberrations chromatiques.
Crédit :
ASM/B. Mollier
Ces aberrations deviennent très vite problématiques lorsqu'on veut atteindre une grande précision.
Un télescope ne présente pas de telles aberrations, l'angle de réflexion d'un rayon lumineux sur une surface métallique ne dépendant pas de la longueur d'onde.
 Perte de lumière
Perte de lumière
Pour arriver jusqu'à l'oculaire, la lumière entrant dans une lunette doit traverser le verre de l'objectif. Le verre n'étant pas totalement transparent, il s'ensuit une perte de luminosité. Celle-ci est d'autant plus grande que l'objectif de la lunette est grand et par conséquent épais.
Si la réflexion sur un miroir n'est certes pas totale, il est facile de la porter à plus de 99%. Une réflexion entraînera moins de perte de photons qu'une transmission à travers du verre. Et quand on sait que dans les télescopes modernes, la lumière peut se réfléchir sur une vingtaine de miroir avant d'être exploitée par un instrument scientifique, on comprend mieux l'intérêt du miroir par rapport à la lentille.
Les avantages et inconvénients en astronomie amateur
Les pages précédentes présentaient les avantages du télescope en astronomie professionnelle. Néanmoins, en astronomie amateur, la lunette à encore toute sa place. Voici une petite liste non exhaustive des avantages et inconvénients des deux instruments.
 Avantages de la lunette
Avantages de la lunette
- La lunette astronomique est un instrument solide et robuste. Elle est moins sujette au désalignement
- Elle nécessite très peu d'entretien, son tube étant hermétique.
- Hermétique toujours, elle est moins sensible à la turbulence.
- Il y a peu de réglage, idéal pour un débutant.
- Son prix est attractif à la base.
- Elle offre de meilleurs grossissements qu'un télescope.
- C'est l'instrument idéal pour l'observation planétaire.
Les inconvénients de la lunette astronomique
- Elle induit des aberrations chromatiques.
- Elle est opaque à certaines longueurs d'onde (UV)
- Plus l'épaisseur de la lentille augmente, plus la lumière est absorbée ou diffusée.
- À diamètre équivalent, elle est beaucoup plus chère qu'un télescope.
- Elle est assez fermée, et donc peu lumineuse.
- Elle ne permet pas d'observer le ciel profond, et est peu adaptée à l'astrophotographie.
 Les avantages du télescope
Les avantages du télescope
- Pas d'aberration chromatique.
- Coût de fabrication moindre à diamètre équivalent.
- Plus grand diamètre et plus grande ouverture, idéal pour le ciel profond et l'astrophotographie.
- Plus compact en configuration Cassegrain.
- Conception compacte et légère pour les Dobson
 Les inconvénients du télescope
Les inconvénients du télescope
- Plus encombrant qu'une petite lunette.
- Plus sensible à la turbulence atmosphérique pour les tubes ouverts.
- Nécessite également plus d'entretien.
- Réglages (collimation) pas toujours évidents.
- Aberration de coma possible.
- Grossissement moindre.
Résumé
 Description d'un télescope
Description d'un télescope
Un télescope est constitué d'un miroir primaire, qui collecte la lumière ; d'un miroir secondaire, qui renvoie la lumière vers l'oculaire et modifie éventuellement la focale du primaire.
Il existe de nombreux types de télescopes, les principaux étant le télescope de Newton, où l'oculaire est placé sur le haut et côté du tube, et le télescope Cassegrain où l'oculaire est placé à la base du tube.
 Grossissement d'un télescope
Grossissement d'un télescope
Comme pour une lunette, le grossissement d'un télescope est le rapport des focales de l'objectif et de l'oculaire,
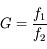
Le grossissement sera d'autant plus grand que la focale du télescope est grande, et celle de l'oculaire réduite.
 Champ d'un télescope
Champ d'un télescope
L'angle de champ d'un télescope est proportionnel à celui de l'oculaire (qui est en général de 40-50°) et inversement proportionnel au grossissement :
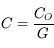
 Lunette ou télescope ?
Lunette ou télescope ?
Si l'astronomie professionnelle a clairement fait le choix du télescope pour des raisons de diamètre et d'aberrations chromatiques, l'astronome amateur pourra encore choisir entre les deux, en fonction de ses besoins.
La lunette est idéale pour le débutant et pour l'observation planétaire.
Le télescope est réservé à l'astronome plus expérimenté, au photographe, ainsi qu'à l'observation du ciel profond.
Conclusion
Nous venons de voir dans ce chapitre qu'avec quelques notions d'optique géométrique, on pouvait comprendre le fonctionnement de nombreux intruments d'optique.
Vous êtes maintenant familier avec les notions de bases de l'optique géométrique, la réflexion et la réfraction. Vous connaissez les lentilles et les miroirs. Et avec cela, vous avez étudié l'appareil photo, l'oeil, la lunette et le télescope.
Vous savez ce qu'est une focale, un grossissement, une ouverture et un angle de vue.
Et c'est fini ? Non, ce n'est que le début. Le dernier chapitre vous initiera à quelques notions d'optique ondulatoire comme la diffraction et les interférences. Et les plus curieux d'entre vous pourront continuer l'année prochaine avec la formation proposée dans le DU Fenêtre sur l'Univers.
Réponses aux exercices
pages_instruments-photo/instru-ap-focale-equivalente.html
Exercice
'Focale équivalente'
- Question 1
Solution :
L'angle de champ est défini par :
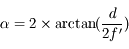
où 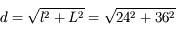
Application numérique :  75°
75°
- Question 2
Solution :
Rebelote 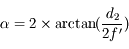 avec
avec 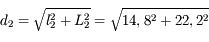
Application numérique : 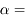 51°
51°
L'angle de champ est plus petit.
- Question 3
Solution :
On repart de la définition de l'angle de champ 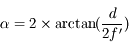
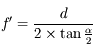
Application numérique :
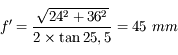
Notre objectif de 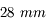 sur notre nouveau boîtier est équivalent à un objectif de focale de
sur notre nouveau boîtier est équivalent à un objectif de focale de 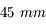 sur un boîtier classique.
sur un boîtier classique.
- Question 4
Solution :
La focale équivalente est de 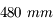 . Avec un "simple" téléobjectif de
. Avec un "simple" téléobjectif de 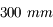 , j'obtiens un téléobjectif bien plus puissant, très pratique pour photographier les animaux en randonnée par exemple.
, j'obtiens un téléobjectif bien plus puissant, très pratique pour photographier les animaux en randonnée par exemple.
- Question 5
Solution :
Il nous faudra un objectif de 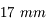 de focale ! C'est-à-dire un objectif de focale beaucoup plus courte que nécessaire. Si un petit capteur est avantageux pour les utilisateurs de téléobjectifs, il l'est beaucoup moins pour les amateurs de grand angle.
de focale ! C'est-à-dire un objectif de focale beaucoup plus courte que nécessaire. Si un petit capteur est avantageux pour les utilisateurs de téléobjectifs, il l'est beaucoup moins pour les amateurs de grand angle.
pages_instruments-photo/instru-ap-ouverture-exo1.html
Exercice
'Ouverture'
pages_instruments-photo/instru-ap-bilan.html
Exercice
'Compact numérique'
- Question 1
Aide :
Le premier est une focale équivalente. Notez que les seconds sont des dénominateurs. Enfin, 49,2 est à peu près égal 12x4,1.
Solution :
Le premier chiffre, 25 mm, est homogène à une focale. C'est en fait la focale équivalente de notre appareil photo compact. Il offrira donc le même angle de champ qu'un réflex équipé d'un objectif de 25 mm.
Les seconds, 1:3.3 - 4.9 sont respectivement les ouvertures de l'objectif à courte et longue focales. Il ouvre donc à 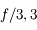 en grand angle, et à
en grand angle, et à 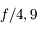 au zoom maximal.
au zoom maximal.
Enfin, les deux derniers chiffres, 4,1 et 49,2 sont les distances focales réelles de l'objectif, exprimées en mm. On en déduit que, si avec une focale de 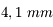 , le compact offre une focale équivalente de
, le compact offre une focale équivalente de 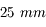 , alors son capteur est beaucoup plus petit qu'un capteur standard
, alors son capteur est beaucoup plus petit qu'un capteur standard 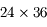 .
.
- Question 2
Solution :
En utilisant le théorème de Thalès, on obtient immédiatement :
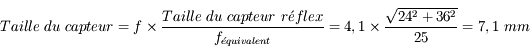
Le capteur mesure 7,1 mm de diagonale.
- Question 3
Aide :
L'appareil affiche un zoom optique de 12x.
Solution :
En zoom maximal, la focale équivalente est de 300 mm.
pages_instruments-oeil/instru-oeil-caracteristiques.html
Exercice
'Angle de champ d'un oeil'
- Question 1
Solution :
En reprenant la formule de l'angle de champ vue au paragraphe précédent,
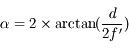 ,
,
on trouve un angle de champ de l'ordre de 40-50°.
- Question 2
Solution :
Cet angle est de l'ordre du degré.
pages_instruments-oeil/instru-oeil-caracteristiques.html
Exercice
'Ouverture de l'oeil'
pages_instruments-oeil/instru-oeil-accomodation-exo1.html
Exercice
'Distance focale de l'oeil'
- Question 1
Solution :
Par définition même de la distance focale image, elle doit être de 2,5 cm.
- Question 2
Solution :
Appliquons la relation de conjugaison de Descartes :
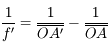 d'où
d'où 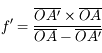
Application numérique
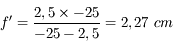
- Question 3
Solution :
On constate d'abord que les distances focales pour regarder à l'infini et de près ne sont pas les mêmes.
Avec une lentille en verre, on ne peut pas changer la distance focale. Il faudrait, pour voir net dans les deux cas, reculer l'écran (la rétine).
Notre oeil ne s'allonge pas quand on regarde de près. C'est le cristallin qui, en se contractant, augmente sa vergence.
pages_instruments-oeil/instru-oeil-myopie-exo.html
Exercice
'Correction de la myopie'
- Question 1
Solution :
L'image se situe dans le plan focal image. Celui-ci étant en avant de la rétine (myopie), l'image ne se forme pas sur cette dernière et sera floue.
Image sans correction
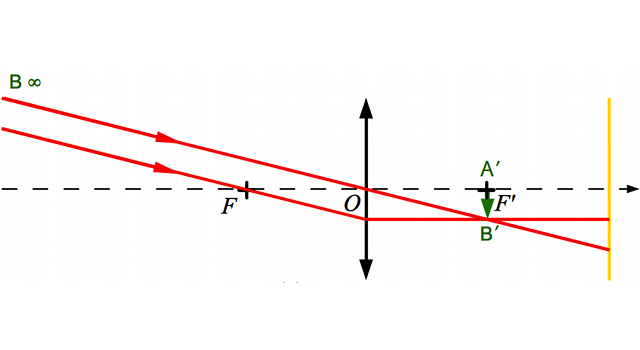
Crédit :
ASM/B. Mollier
- Question 2
Solution :
L'image est située en amont de la lentille divergente. Elle est virtuelle et droite.
Image à travers la paire de lunettes
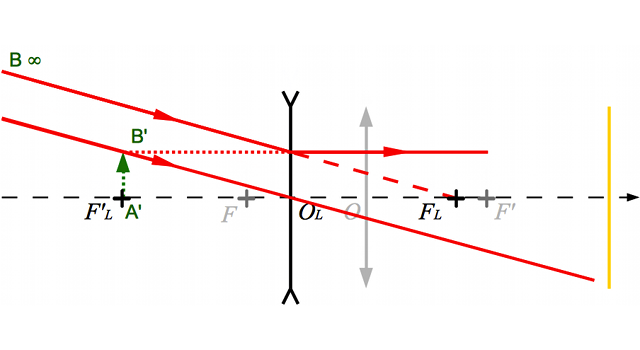
Crédit :
ASM/B. Mollier
- Question 3
Solution :
Si vous avez bien travaillé, l'image est cette fois-ci située sur la rétine. L'objet n'est plus vu flou. L'image est réelle et inversée.
Image corrigée
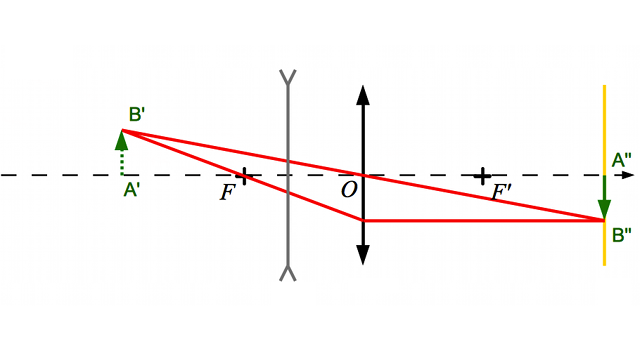
Crédit :
ASM/B. Mollier
pages_instruments-oeil/instru-oeil-hypermetrope-exo.html
Exercice
'Correction de l'hypermétropie'
- Question 1
Aide :
L'objet étant à distance fini, l'oeil accommode.
Solution :
On utilise la relation de conjugaison de Descartes :
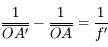 d'où
d'où 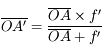
Application numérique :
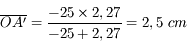
Même en accommodant au maximum, l'image se forme après la rétine.
- Question 2
Solution :
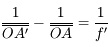 d'où
d'où 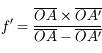
Application numérique :
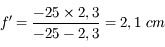
La distance focale doit être plus courte que celle du cristallin.
- Question 3
Aide :
Reprenez la distance focale calculée à la question précédente.
Solution :
Les lentilles sont supposées accolées, donc :
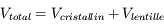 d'où
d'où 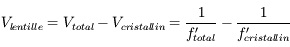
Application numérique :
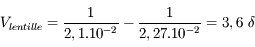
Il faut des lentilles de contact de vergence 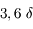 . Cette vergence est positive, il s'agit donc de lentilles convergentes.
. Cette vergence est positive, il s'agit donc de lentilles convergentes.
pages_instruments-oculaire/instru-loupe-aa-exo.html
Exercice
'Tour Eiffel'
pages_instruments-lunette/instru-lunette-grsst-exo.html
Exercice
'Observation de Jupiter'
- Question 1
Aide :
On parle d'opposition quand la planète est au plus proche de la Terre.
Aide :
Le rayon équatorial de Jupiter est de 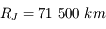 . À l'opposition, elle se situe à environ
. À l'opposition, elle se situe à environ 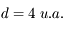 de la Terre.
de la Terre.
Solution :
Par définition du diamètre apparent :

Application numérique :

- Question 2
Solution :
Le grossissement est inversement proportionnel à la focale de l'oculaire. Vous devrez utiliser l'oculaire de  pour avoir le plus fort grossissement. Il sera alors de
pour avoir le plus fort grossissement. Il sera alors de  .
.
- Question 3
Solution :
Le diamètre de Jupiter dans l'oculaire vaut
 avec
avec 
Application numérique

- Question 4
Aide :
La résolution de l'oeil, c'est-à-dire la taille du plus petit détail visible, est de l'ordre de 1'.
Solution :
À l'opposition, la taille apparente de la tache est supérieure à la dizaine de minutes d'angle, elle sera donc visible à ce grossissement.
pages_instruments-lunette/instru-lunette-champ-exo1.html
Exercice
'Observation de la Lune'
pages_instruments-lunette/instru-lunette-bilan.html
Exercice
'La grande lunette de Meudon'
- Question 1
Solution :
Par définition du grossissement

Le grossissement est de 400 !
- Question 2
Aide :
Saturne est située à 10 u.a. du Soleil, et possède un diamètre de  . Celui des anneaux est le double.
. Celui des anneaux est le double.
Solution :
À l'opposition, la distance Terre-Saturne est de 9 u.a. soit  . On en déduit son angle apparent :
. On en déduit son angle apparent :
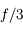
Le diamètre apparent de Saturne est de 18 secondes d'angle. Avec ses anneaux, elle mesure environ 36 secondes d'angle.
Dans la lunette, elle mesure alors 400 fois plus, soit 2 degrés.
- Question 3
Aide :
La division de Cassini mesure 5000 km de large.
Solution :
L'angle apparent de la division est de l'ordre de  . À la lunette, on la verra sous un angle de 5 minutes d'angle, ce qui largement au dessus de la résolution de l'oeil.
. À la lunette, on la verra sous un angle de 5 minutes d'angle, ce qui largement au dessus de la résolution de l'oeil.
- Question 4
Solution :
L'angle de champ de la lunette est de 0,13°. Saturne est visible en entier parce que sa taille fait 36 arcsec avec les anneaux. La planète est 13 fois plus petite que l'angle de champ de la lunette.
- Question 5
Aide :
Les télescopes modernes possèdent des ouvertures de l'ordre de  .
.
Solution :
Pour obtenir l'ouverture, on divise le diamètre de la lunette par sa focale. On obtient donc des ouvertures respectives de  et
et  pour les deux lunettes. Ces lunettes sont très fermées en comparaison des télescopes de maintenant. Il faudra donc poser beaucoup plus longtemps pour obtenir la même quantité de photons issus d'un point de l'astre.
pour les deux lunettes. Ces lunettes sont très fermées en comparaison des télescopes de maintenant. Il faudra donc poser beaucoup plus longtemps pour obtenir la même quantité de photons issus d'un point de l'astre.
 Différents types de systèmes optiques
Différents types de systèmes optiques Dans ce chapitre...
Dans ce chapitre... Prérequis
Prérequis







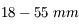 , téléobjectif de
, téléobjectif de 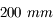 , grand angulaire de
, grand angulaire de 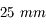 ... qu'est-ce que tout ça ?
... qu'est-ce que tout ça ?

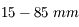 ?
?
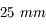 veut dire que notre objectif est équivalent à une lentille mince convergente de distance focale image
veut dire que notre objectif est équivalent à une lentille mince convergente de distance focale image 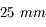 . Quand au téléobjectif de
. Quand au téléobjectif de 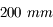 , il sera équivalent à une lentille mince convergente de vergence moindre, puisque sa distance focale sera de
, il sera équivalent à une lentille mince convergente de vergence moindre, puisque sa distance focale sera de 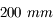 .
.
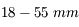 par exemple) et au zoom universel (
par exemple) et au zoom universel (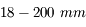 ), en jouant sur le déplacement de lentilles à l'intérieur, on peut faire varier leur distance focale. C'est l'avantage d'avoir un système à plusieurs lentilles par rapport à une unique lentille pour laquelle cette grandeur est fixe.
), en jouant sur le déplacement de lentilles à l'intérieur, on peut faire varier leur distance focale. C'est l'avantage d'avoir un système à plusieurs lentilles par rapport à une unique lentille pour laquelle cette grandeur est fixe.

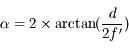 , où
, où 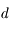 est la diagonale du capteur,
est la diagonale du capteur, 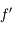 la focale.
la focale.
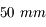 qui offre un champ comparable à celui d'un oeil humain.
qui offre un champ comparable à celui d'un oeil humain.

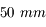 dont l'angle de champ est équivalent à celui de l'oeil.
dont l'angle de champ est équivalent à celui de l'oeil.

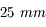 .
.

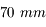 .
.

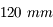 .
.

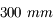 .
.

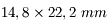 .
.

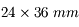 comme les argentiques, mais
comme les argentiques, mais 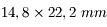 .
.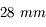 de focale. Rappelez quel serait l'angle de champ avec un capteur
de focale. Rappelez quel serait l'angle de champ avec un capteur 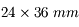 .
.
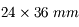 . C'est ce qu'on appellera la focale utile (ou équivalente).
. C'est ce qu'on appellera la focale utile (ou équivalente).
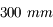 . Commentez.
. Commentez.
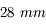 , quel objectif dois-je acheter ? Concluez.
, quel objectif dois-je acheter ? Concluez.
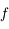 sur un nombre. Nous allons voir pourquoi.
sur un nombre. Nous allons voir pourquoi.
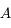 mesure le rapport entre le diamètre
mesure le rapport entre le diamètre 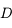 de l'objectif (du collecteur de lumière en général) et sa focale
de l'objectif (du collecteur de lumière en général) et sa focale 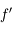 :
:
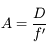

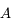 mesure le rapport entre le diamètre
mesure le rapport entre le diamètre 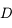 de l'objectif (du collecteur de lumière en général) et sa focale
de l'objectif (du collecteur de lumière en général) et sa focale 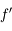 :
: 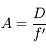
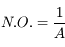
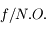
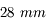 de focale, avec un diaphragme de
de focale, avec un diaphragme de 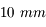 de diamètre, l'angle d'ouverture vaut
de diamètre, l'angle d'ouverture vaut 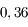 et son ouverture vaut 2,8. On parle donc d'objectif ouvert à
et son ouverture vaut 2,8. On parle donc d'objectif ouvert à 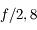 .
.
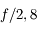 veut simplement dire que le diamètre du diaphragme est 2,8 fois plus petit que la focale.
veut simplement dire que le diamètre du diaphragme est 2,8 fois plus petit que la focale.
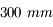 de focale, dont le diamètre est
de focale, dont le diamètre est 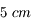 . Quelle pourra être l'ouverture maximale ?
. Quelle pourra être l'ouverture maximale ?



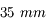 .
.
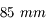 .
.

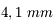 , le compact offre une focale équivalente de
, le compact offre une focale équivalente de 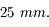 Déduisez-en la taille du capteur.
Déduisez-en la taille du capteur.



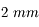 à
à 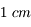 .
.
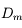 appelée punctum remotum, notée
appelée punctum remotum, notée  .
.
 .
.


 est également plus proche. Un myope peut lire de plus près et est un peu moins sensible à la presbytie.
est également plus proche. Un myope peut lire de plus près et est un peu moins sensible à la presbytie.

 est situé derrière l'oeil ! Si si ! On plaisante à ce sujet en disant qu'un hypermétrope peut voir derrière lui. Vous l'aurez compris, le
est situé derrière l'oeil ! Si si ! On plaisante à ce sujet en disant qu'un hypermétrope peut voir derrière lui. Vous l'aurez compris, le  se situe dans l'espace image. C'est-à-dire qu'il est possible, pour un oeil hypermétrope de former l'image d'objets virtuels.
se situe dans l'espace image. C'est-à-dire qu'il est possible, pour un oeil hypermétrope de former l'image d'objets virtuels.
 est plus éloigné que la normale.
est plus éloigné que la normale.

 est à l'infini et le
est à l'infini et le  à environ
à environ 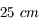 . Au milieu l'oeil myope. Le
. Au milieu l'oeil myope. Le  n'est plus à l'infini : on voit mal de loin. Le
n'est plus à l'infini : on voit mal de loin. Le  s'est rapproché de l'oeil. Un myope peut lire de plus près. En bas, un oeil hypermétrope. le
s'est rapproché de l'oeil. Un myope peut lire de plus près. En bas, un oeil hypermétrope. le  est passé dans l'espace objet virtuel, il est situé derrière le cristallin. Le
est passé dans l'espace objet virtuel, il est situé derrière le cristallin. Le  s'est éloigné : on voit mal de près.
s'est éloigné : on voit mal de près.
 reste à l'infini alors que le
reste à l'infini alors que le  s'éloigne progressivement.
s'éloigne progressivement.

 situé à l'infini à travers l'oeil seul. On ne s'occupera pas, dans cette question, de la lentille divergente en bleue. Cette image est-elle située sur la rétine ?
situé à l'infini à travers l'oeil seul. On ne s'occupera pas, dans cette question, de la lentille divergente en bleue. Cette image est-elle située sur la rétine ?
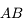 à travers les lunettes et l'oeil, nous allons procéder par étapes. Tout d'abord, nous allons tracer l'image
à travers les lunettes et l'oeil, nous allons procéder par étapes. Tout d'abord, nous allons tracer l'image 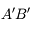 de l'objet à travers la lentille divergente. Puis, dans un second temps, nous allons considérer cette image
de l'objet à travers la lentille divergente. Puis, dans un second temps, nous allons considérer cette image 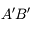 comme étant un objet pour la lentille convergente, et en tracer son image
comme étant un objet pour la lentille convergente, et en tracer son image 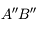 .
.
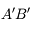 de l'objet à travers la lentille divergente. Où est-elle ? Est-elle réelle ? virtuelle ? droite ? inversée ?
de l'objet à travers la lentille divergente. Où est-elle ? Est-elle réelle ? virtuelle ? droite ? inversée ?
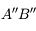 de l'objet
de l'objet 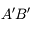 à travers la lentille convergente. Où est située cette image ? Est-elle réelle ? virtuelle ? droite ? inversée ?
à travers la lentille convergente. Où est située cette image ? Est-elle réelle ? virtuelle ? droite ? inversée ?
 et
et 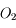 de celles-ci, devant toutes les grandeurs caractéristiques du système optique. Bref,
de celles-ci, devant toutes les grandeurs caractéristiques du système optique. Bref, 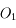 et
et 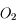 sont confondus.
sont confondus.
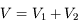
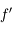 peut être déduite par :
peut être déduite par :
 et
et  , on obtient :
, on obtient :
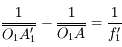 et
et 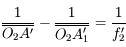
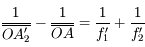
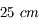 de l'oeil. Où se situe son image ? Est-elle sur la rétine ?
de l'oeil. Où se situe son image ? Est-elle sur la rétine ?
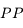 . Cependant, cela entraîne une fatigue de l'oeil, et, avec l'âge, ce point s'éloigne.
. Cependant, cela entraîne une fatigue de l'oeil, et, avec l'âge, ce point s'éloigne.
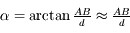
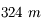 et est distante de
et est distante de 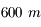 de l'esplanade.
de l'esplanade.
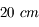 pour obtenir le même angle apparent ?
pour obtenir le même angle apparent ?

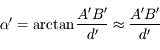

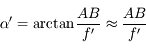
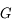 comme étant le rapport de ces deux quantités :
comme étant le rapport de ces deux quantités :
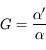
 est grand) plus grand sera le diamètre apparent de l'image.
est grand) plus grand sera le diamètre apparent de l'image.


 finie, le diamètre apparent
finie, le diamètre apparent  dépend de la position de l'oeil. Or il serait bon d'avoir un grossissement ne dépendant que de l'instrument. Cela nous permettra de les comparer entre eux.
dépend de la position de l'oeil. Or il serait bon d'avoir un grossissement ne dépendant que de l'instrument. Cela nous permettra de les comparer entre eux.
 , c'est-à-dire à 25 cm de l'oeil.
, c'est-à-dire à 25 cm de l'oeil.
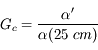 avec
avec 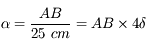
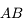 de l'objet :
de l'objet :
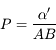
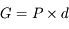
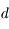 tend vers l'infini. La puissance est donc toujours nulle.
tend vers l'infini. La puissance est donc toujours nulle.
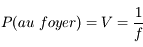
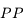 et le
et le 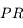 pour être vue nette. Sa distance est comprise entre
pour être vue nette. Sa distance est comprise entre 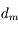 et
et 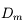 .
.
 et du
et du  par loupe. Elle dépend bien sûr de la position de l'oeil par rapport à la loupe.
par loupe. Elle dépend bien sûr de la position de l'oeil par rapport à la loupe.
 et
et  vaut respectivement :
vaut respectivement :
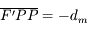 et
et 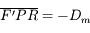 .
.
 et
et  sont respectivement :
sont respectivement :
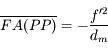 et
et 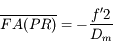
![= [-\frac{f'^2}{d_m}-f',-\frac{f'^2}{D_m}-f']](../pages_instruments-oculaire/equations_instruments-oculaire/equation35.png)
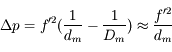
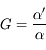
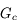 comme étant le cas particulier du grossissement d'un objet situé à
comme étant le cas particulier du grossissement d'un objet situé à 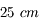 de l'oeil.
de l'oeil.
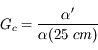
 comme étant le rapport entre la taille de l'objet et le diamètre apparent de l'image.
comme étant le rapport entre la taille de l'objet et le diamètre apparent de l'image.
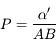


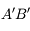 à son foyer.
à son foyer.

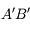 étant en général petite, il faut la regarder avec une loupe : l'oculaire. Ce dernier grossit l'image et la rejette à l'infini.
étant en général petite, il faut la regarder avec une loupe : l'oculaire. Ce dernier grossit l'image et la rejette à l'infini.
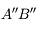 est d'autant plus grande que la focale de l'oculaire est courte.
est d'autant plus grande que la focale de l'oculaire est courte.
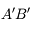 constitue un objet virtuel pour l'oculaire.
constitue un objet virtuel pour l'oculaire.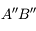 à l'infini, nous avons placé le foyer principal objet sur l'image intermédiaire.
à l'infini, nous avons placé le foyer principal objet sur l'image intermédiaire.
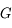
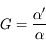
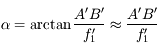 et
et 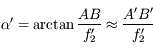
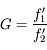
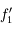 ) et de l'oculaire (
) et de l'oculaire (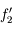 )
)
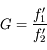

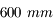 de focale (il s'agit ici de la focale de l'objectif).
de focale (il s'agit ici de la focale de l'objectif).

 de la table équatoriale, à l'observatoire de Meudon. On y voit la grande tache rouge (bande rouge du haut), ainsi qu'une tempête (bande rouge du bas).
de la table équatoriale, à l'observatoire de Meudon. On y voit la grande tache rouge (bande rouge du haut), ainsi qu'une tempête (bande rouge du bas).
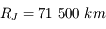 . À l'opposition, elle se situe à environ
. À l'opposition, elle se situe à environ 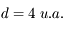 de la Terre.
de la Terre.
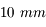 ,
, 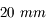 et
et 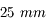 de focale respectivement. Lequel devez-vous utiliser pour obtenir le meilleur grossissement ?
de focale respectivement. Lequel devez-vous utiliser pour obtenir le meilleur grossissement ?
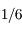 du diamètre de Jupiter. Sera-t-elle visible dans cet instrument ?
du diamètre de Jupiter. Sera-t-elle visible dans cet instrument ?




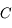 d'une lunette astronomique (et d'un télescope) est le rapport du champ de l'oculaire
d'une lunette astronomique (et d'un télescope) est le rapport du champ de l'oculaire 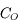 par le grossissement
par le grossissement 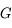 :
:
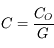

 de focale, ainsi qu'un oculaire de
de focale, ainsi qu'un oculaire de  de focale et de
de focale et de 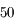 ° de champ.
° de champ.
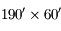 .
.
 situé sur l'axe optique.
situé sur l'axe optique.

 est celle qui limite le plus la taille du faisceau. Le faisceau rouge, prenant appui sur la monture
est celle qui limite le plus la taille du faisceau. Le faisceau rouge, prenant appui sur la monture 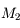 est vignété par
est vignété par 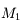 . Le faisceau bleu, prenant appui sur la monture
. Le faisceau bleu, prenant appui sur la monture 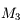 est vignété par
est vignété par 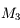 et
et 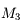 . La lentille
. La lentille 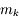 joue le rôle de diaphragme d'ouverture.
joue le rôle de diaphragme d'ouverture.
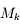 ).
).
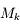 traversera toutes les montures réelles
traversera toutes les montures réelles 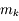 . Trouver le diaphragme d'ouverture
. Trouver le diaphragme d'ouverture 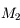 revient à chercher le conjugué
revient à chercher le conjugué 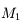 dont le diamètre est le plus petit.
dont le diamètre est le plus petit.

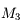 à travers
à travers 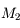 et
et 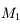 à travers
à travers 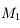 et
et 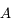 .
. 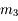 est son propre antécédent. On cherche ensuite lequel de ces antécédents limite le plus le faisceau issu de
est son propre antécédent. On cherche ensuite lequel de ces antécédents limite le plus le faisceau issu de 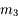 . Ici, c'est
. Ici, c'est 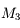 .
. 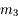 est appelé pupille d'entrée, et son image
est appelé pupille d'entrée, et son image 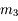 est appelée diaphragme d'ouverture.
est appelée diaphragme d'ouverture.
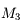 .
.  est appelé pupille d'entrée et
est appelé pupille d'entrée et  diaphragme d'ouverture.
diaphragme d'ouverture.
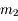 , hors de l'axe optique. Intéressons-nous au rayon issu de
, hors de l'axe optique. Intéressons-nous au rayon issu de 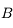 et passant par le centre de la pupille d'entrée et donc au centre du diaphragme d'ouverture et de la pupille de sortie. Il est appelé rayon moyen ou rayon principal.
et passant par le centre de la pupille d'entrée et donc au centre du diaphragme d'ouverture et de la pupille de sortie. Il est appelé rayon moyen ou rayon principal.

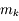 , appelé lucarne d'entrée, est celui qui limite le plus l'angle de champ.
, appelé lucarne d'entrée, est celui qui limite le plus l'angle de champ.
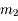 jusqu'à ce que le rayon rayon principal soit intercepté par un des conjugués
jusqu'à ce que le rayon rayon principal soit intercepté par un des conjugués 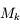 (ici
(ici 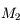 ).
).
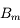 (ici
(ici 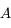 ) est appelé diaphragme de champ.
) est appelé diaphragme de champ.
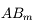 . Il délimite le champ moyen de l'instrument. Le champ moyen est le disque de centre
. Il délimite le champ moyen de l'instrument. Le champ moyen est le disque de centre 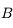 et de rayon
et de rayon 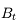 .
.

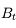 , de telle sorte que le rayon qui en est issu passe par le bord de la lucarne d'entrée et la pupille d'entrée (en vert sur la figure). Il délimite également un champ, plus petit que le précédent appelé champ de pleine lumière.
, de telle sorte que le rayon qui en est issu passe par le bord de la lucarne d'entrée et la pupille d'entrée (en vert sur la figure). Il délimite également un champ, plus petit que le précédent appelé champ de pleine lumière.


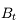 .
.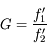 est un point particulier : les rayons qui en sont issus passent par le bord supérieur de la lucarne d'entrée puis par le bord inférieur de la pupille d'entrée. Bref, le faisceau issu de
est un point particulier : les rayons qui en sont issus passent par le bord supérieur de la lucarne d'entrée puis par le bord inférieur de la pupille d'entrée. Bref, le faisceau issu de 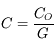 passant par les lucarne et pupille d'entrée se résume à un seul rayon lumineux.
passant par les lucarne et pupille d'entrée se résume à un seul rayon lumineux.




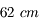
 de diamètre, l'autre
de diamètre, l'autre 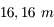 . Elles possèdent toutes deux une focale de
. Elles possèdent toutes deux une focale de 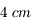 .
.

 , celle de l'oculaire est de
, celle de l'oculaire est de 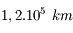 . Calculez le grossissement.
. Calculez le grossissement.
 . Celui des anneaux est le double.
. Celui des anneaux est le double.
 .
.

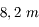 de diamètre !
de diamètre !



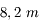 de diamètre tout de même ! Le petit miroir au centre est un miroir tertiaire, qui permet de renvoyer la lumière sur les côtés. Il peut aussi être escamoté pour passer en mode Cassegrain.
de diamètre tout de même ! Le petit miroir au centre est un miroir tertiaire, qui permet de renvoyer la lumière sur les côtés. Il peut aussi être escamoté pour passer en mode Cassegrain.


 de l'objectif par la focale
de l'objectif par la focale  de l'oculaire.
de l'oculaire.
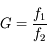
 , on segmente le miroir. Il n'est plus monolithique, mais composé de plusieurs pièces hexagonales, assemblées comme un puzzle. Les télescopes actuels mesurent
, on segmente le miroir. Il n'est plus monolithique, mais composé de plusieurs pièces hexagonales, assemblées comme un puzzle. Les télescopes actuels mesurent  de diamètre. Et on ne s'arrêtera pas là. Des projets de télescopes de
de diamètre. Et on ne s'arrêtera pas là. Des projets de télescopes de  à
à 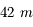 sont en cours de réalisation.
sont en cours de réalisation.

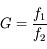
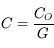
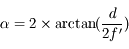
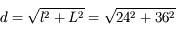
 75°
75°
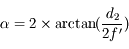 avec
avec 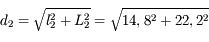
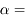 51°
51°
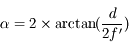
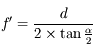
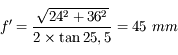
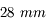 sur notre nouveau boîtier est équivalent à un objectif de focale de
sur notre nouveau boîtier est équivalent à un objectif de focale de 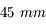 sur un boîtier classique.
sur un boîtier classique.
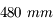 . Avec un "simple" téléobjectif de
. Avec un "simple" téléobjectif de 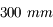 , j'obtiens un téléobjectif bien plus puissant, très pratique pour photographier les animaux en randonnée par exemple.
, j'obtiens un téléobjectif bien plus puissant, très pratique pour photographier les animaux en randonnée par exemple.
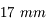 de focale ! C'est-à-dire un objectif de focale beaucoup plus courte que nécessaire. Si un petit capteur est avantageux pour les utilisateurs de téléobjectifs, il l'est beaucoup moins pour les amateurs de grand angle.
de focale ! C'est-à-dire un objectif de focale beaucoup plus courte que nécessaire. Si un petit capteur est avantageux pour les utilisateurs de téléobjectifs, il l'est beaucoup moins pour les amateurs de grand angle.
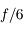 .
.
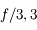 en grand angle, et à
en grand angle, et à 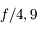 au zoom maximal.
au zoom maximal.
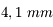 , le compact offre une focale équivalente de
, le compact offre une focale équivalente de 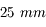 , alors son capteur est beaucoup plus petit qu'un capteur standard
, alors son capteur est beaucoup plus petit qu'un capteur standard 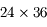 .
.
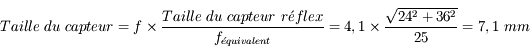
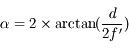 ,
,
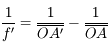 d'où
d'où 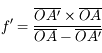
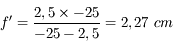



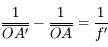 d'où
d'où 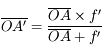
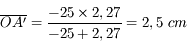
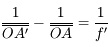 d'où
d'où 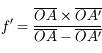
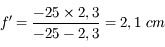
 d'où
d'où 
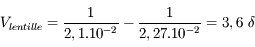
 . Cette vergence est positive, il s'agit donc de lentilles convergentes.
. Cette vergence est positive, il s'agit donc de lentilles convergentes.


 pour avoir le plus fort grossissement. Il sera alors de
pour avoir le plus fort grossissement. Il sera alors de  .
.
 avec
avec 



 de la lunette est le champ de l'oculaire divisé par le grossissement. Il vaut donc
de la lunette est le champ de l'oculaire divisé par le grossissement. Il vaut donc 
 , elle ne sera pas visible en entier dans la lunette, il faudra préférer un oculaire de
, elle ne sera pas visible en entier dans la lunette, il faudra préférer un oculaire de  qui donnera un champs de
qui donnera un champs de  . M3 ne sera pas visible entierrement, même avec un oculaire de
. M3 ne sera pas visible entierrement, même avec un oculaire de  .
.

 . On en déduit son angle apparent :
. On en déduit son angle apparent :
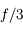
 . À la lunette, on la verra sous un angle de 5 minutes d'angle, ce qui largement au dessus de la résolution de l'oeil.
. À la lunette, on la verra sous un angle de 5 minutes d'angle, ce qui largement au dessus de la résolution de l'oeil.
 et
et  pour les deux lunettes. Ces lunettes sont très fermées en comparaison des télescopes de maintenant. Il faudra donc poser beaucoup plus longtemps pour obtenir la même quantité de photons issus d'un point de l'astre.
pour les deux lunettes. Ces lunettes sont très fermées en comparaison des télescopes de maintenant. Il faudra donc poser beaucoup plus longtemps pour obtenir la même quantité de photons issus d'un point de l'astre.