Dans le chapitre précédent, nous avons vu les réflexions et la réfraction sur des dioptres et des miroirs plans. Mais il suffit de regarder n'importe quel instrument d'optique pour voir qu'ils ne sont pas uniquement composés de ce type d'optiques. Les notions précédemment abordées ne sont donc pas suffisantes pour décrire ces instruments.
Prenons un verre de lunette. Il n'est pas plan. Sa surface est courbe. Les objets à travers y paraissent déformés. Idem avec une loupe. Ce qu'on y voit à travers nous apparaît tantôt plus gros, tantôt flou, ou parfois même plus petit et renversé. Les rétroviseurs extérieurs d'une voiture comportent en général une partie courbe sur leur extrémité. La voiture qui nous suit y apparaît plus éloignée que dans le rétroviseur intérieur. Tous ces objets du quotidien, ainsi que d'autres instruments comme les appareils photos, les télescopes ou les microscopes, sont en fait constitués de lentilles (des dioptres dont la surface est courbe) ou des miroirs aux formes sphériques, paraboliques ou même hyperboliques.
Nous avons commencé à voir, au chapitre précédent, les phénomènes mis en jeux dans ces systèmes. Nous n'allons pas nous arrêter en si bon chemin. Dans les chapitres qui suivent, nous allons étudier ces nouveaux éléments, en commençant par les lentilles minces. Nous aborderons aussi la formation des images en optique. À partir de là, nous pourrons commencer à étudier des systèmes optiques plus complexe comme les lunettes astronomiques, les appareils photos, l'oeil...
Des lentilles, des tas de lentilles !

Crédit :
B. Mollier
 Qu'est-ce qu'une lentille ?
Qu'est-ce qu'une lentille ?
Qu'est-ce qu'on appelle une lentille ? Par lentille, j'entends bien sûr une lentille en optique, et non l'une des espèces de fabacées. Prenons en deux exemples. Dans une main, une loupe, dans l'autre, une paire de lunettes pour myope. Elles sont toutes les deux en verre, transparentes, et délimitées par au moins une surface courbe, parfois deux.
 Définition
Définition
Nous appellerons désormais une lentille sphérique une portion de MTHI (ici notre verre), limité par 2 dioptres dont l'un au moins est sphérique. Remarquons tout de suite qu'une lentille n'est par forcément sphérique. Il en existe, pour ne citer qu'elles, des cylindriques. Nous nous limiterons par contre, dans ce chapitre, aux lentilles sphériques.
Lunettes correctrices

Crédit :
B. Mollier
Définition : les lentilles minces
Pour simplifier encore notre étude, nous nous limiterons au cas des lentilles dites minces. C'est-à-dire dont l'épaisseur est faible devant le rayon de courbure des dioptres.
Lentille mince
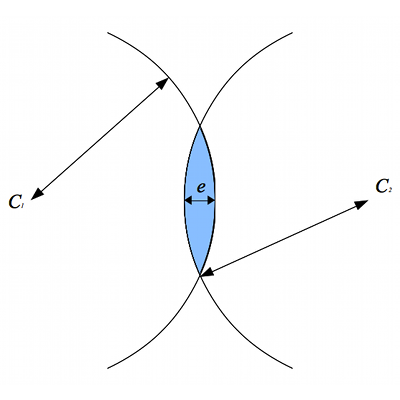
Une lentille est considérée comme mince lorsque son épaisseur
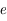
est petite devant le rayon de courbure des dioptres et devant la distance entre les centres
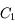
et
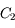
.
Crédit :
ASM/B. Mollier
 Conséquence
Conséquence
La première conséquence, illustrée ci-dessous, est que tout rayon lumineux passant par le centre d'une lentille, ne sera pas dévié. En effet, c'est comme s'il traversait une lame de verre d'épaisseur nulle.
Lentille mince
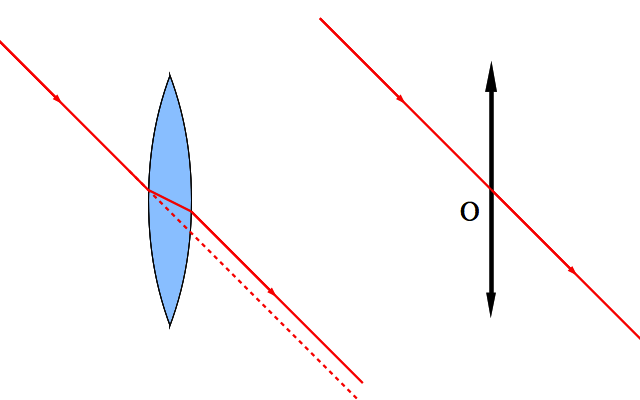
Les rayons lumineux passant par le centre de la lentille, supposée mince, ne sont pas déviés.
Crédit :
ASM/B. Mollier
 Expérience 1 : une lentille au Soleil
Expérience 1 : une lentille au Soleil
Réalisons une petite expérience. Mettons une loupe au Soleil. La lumière est focalisée en un point. Très amusant pour mettre le feu à une feuille de papier. Mais si on essaie avec le verre de lunette... On a beau déplacer celui-ci, aucune tache de lumière ne se forme. Les rayons du Soleil ne sont pas focalisés par celui-ci. Aurions-nous à faire à deux types de lentilles ?
 Expérience 2 : observation des rayons lumineux
Expérience 2 : observation des rayons lumineux
Une deuxième expérience nous le confirme. Les lentilles de type loupe font converger la lumière. Les lentilles de type verre de lunettes pour la myopie font diverger les rayons lumineux.
 Définitions : lentilles convergentes et divergentes
Définitions : lentilles convergentes et divergentes
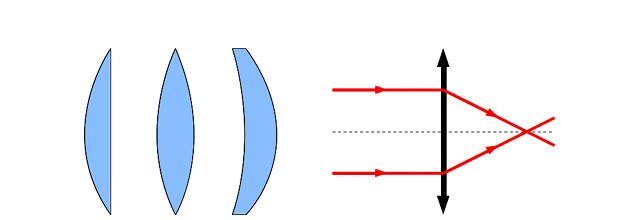
Dans le cas de la loupe, les rayons arrivant parallèles en amont sont focalisés en sortie de la lentille. Ce premier type de lentille est appelé lentille convergente.
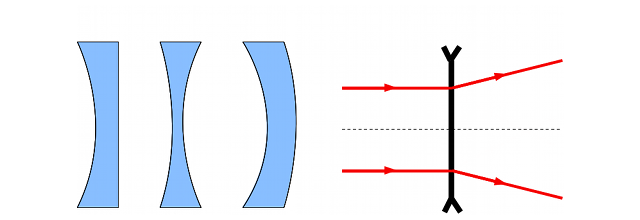
Dans le cas du verre de lunette, les rayons s'écartent les uns des autres après passage par la lentille. Ils divergent. Ces lentilles sont appelées lentilles divergentes.
 Différences entre les lentilles convergentes et divergentes
Différences entre les lentilles convergentes et divergentes
Si on regarde une coupe de ces lentilles, on voit d'où vient cette différence. On constate que les lentilles convergentes possèdent des bords plus fins que le centre. Pour les lentilles divergentes, c'est l'inverse, les bords sont plus épais que le centre.
Les différents types de lentilles
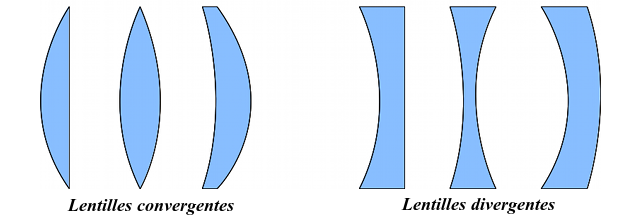
À gauche, les lentilles convergentes. À droite, les lentilles divergentes.
Crédit :
ASM/B. Mollier
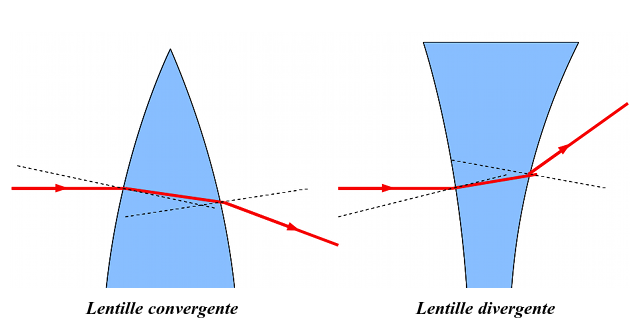
Lorsqu'un rayon arrivant au-dessus de l'axe de symétrie de la lentille (que nous appellerons axe optique) atteint la surface d'une lentille convergente, les lois de la réfraction nous disent qu'il est dévié vers l'axe optique. Le rayon se rapproche de celui-ci. Il converge.
Dans le cas d'un lentille divergente, le rayon incident est quant à lui dévié en s'écartant de l'axe optique.
Pourquoi une lentille convergente est convergente et vice et versa ?
Crédit :
ASM/B. Mollier
 Lentille convergente utilisée comme une loupe
Lentille convergente utilisée comme une loupe
Prenons une lentille convergente. Utilisons la d'abord comme une loupe. En observant un objet (un timbre, par exemple) dans la direction perpendiculaire à lui, on peut obtenir, en plaçant judicieusement la loupe, une image nette et agrandie du timbre. Nous nous trouvons donc dans des conditions de stigmatisme et d'aplanétisme au moins approché. Si on s'amuse à déplacer un écran derrière notre lentille pour obtenir une image de notre timbre, c'est peine perdue. Nous avons donc une image virtuelle, l'objet étant tout ce qu'il y a de plus réel.
 Lentille convergente utilisée comme un projecteur
Lentille convergente utilisée comme un projecteur
Remplaçons cette fois le timbre par un objet rétroéclairé (les opticiens aiment bien utiliser un F éclairé par l'arrière). Plaçons un écran suffisamment loin de lui. Si on déplace la lentille, on trouve deux positions où l'on obtient une image inversée du F, tantôt plus grande, tantôt plus petite. On a donc cette fois-ci une image réelle. Tiens, une lentille convergente peut produire les deux types d'images à partir d'un objet réel. Nous allons détailler cela dans la suite.
 Foyer principal image
Foyer principal image
Considérons un faisceau parallèle (objet à l'infini) et parallèle à l'axe optique (cas du Soleil à travers une loupe) et observons ce qui se passe. Dans le cas d'une lentille convergente, tous les rayons convergent en un point. Nous appellerons ce point foyer principal image. Ce point est l'image réelle d'un point situé à l'infini. Dans le cas d'une lentille divergente, tous les rayons divergent. Cependant, ils semblent tous provenir d'un point situé en amont de la lentille (il suffit de les prolonger). Nous appellerons également ce point foyer principal image. Il est l'image virtuelle d'un point situé à l'infini.
Qu'advient-il d'un faisceau parallèle au passage d'une lentille ?

Crédit :
B. Mollier
 Définition
Définition
Le foyer principal image est le point image d'un point objet situé à l'infini sur l'axe optique.
Foyer principal objet
Par retour inverse de la lumière, si on place une source ponctuelle au foyer image, les rayons ressortiront parallèles. La lentille étant symétrique, on peut la retourner. Il existe donc un point où si l'on place une source ponctuelle, les rayons issus de ce point seront parallèles entre eux et parallèles à l'axe optique. Ce point est appelé foyer principal objet. Il est le symétrique par rapport à la lentille de foyer principal image. Dans le cas d'une lentille convergente, ce point est le point objet réel donnant une image à l'infini. Dans le cas d'une lentille divergente, ce point est le point objet virtuel donnant une image à l'infini.
Foyer principal objet

Le foyer principal objet est l'antécédent d'un point image situé à l'infini sur l'axe optique.
Crédit :
B. Mollier
 Définition
Définition
Le foyer principal objet est l'antécédent d'un point image situé à l'infini sur l'axe optique.
 Distance focale image
Distance focale image
On appelle distance focale image la distance séparant le centre de la lentille au foyer image. On la note 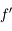 . C'est une quantité algébrique, c'est-à-dire qu'on la compte positivement dans le sens de propagation de la lumière.
. C'est une quantité algébrique, c'est-à-dire qu'on la compte positivement dans le sens de propagation de la lumière. 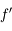 est positif dans le cas d'une lentille convergente et négatif dans le cas d'une divergente.
est positif dans le cas d'une lentille convergente et négatif dans le cas d'une divergente.
Distance focale image
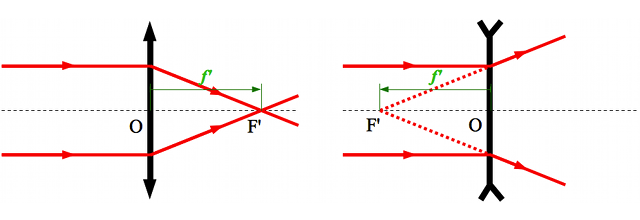
En vert, on définit la distance focale image
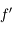
comme étant la distance du centre
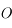
de la lentille au foyer principal image
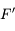
. Notez le sens de la flèche. Dans le cas d'une lentille convergente, elle est dans le même sens que celui de la propagation de la lumière. Cette distance est alors positive. Dans le cas de la lentille divergente, cette flèche est dans le sens opposé à la propagation de la lumière. Cette distance est alors comptée négativement. Pour plus d'information sur ces notions de distances positives et négatives, lisez cette
page.
Crédit :
ASM/B. Mollier
 Distance focale objet
Distance focale objet
De la même manière, on définit la distance focale objet comme étant la distance séparant le centre de la lentille et le foyer principal objet. Les deux foyers 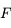 et
et 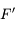 étant symétriques par rapport au centre
étant symétriques par rapport au centre 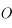 , on obtient
, on obtient 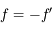 .
.
Distance focale objet
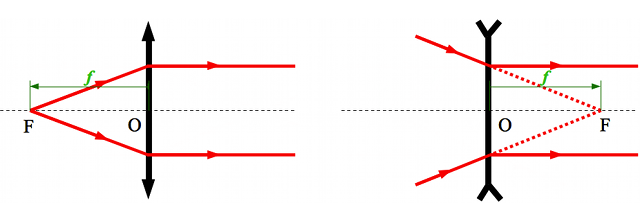
On définit la distance focale objet
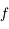
comme étant la distance séparant le centre de la lentille et le foyer principal objet. Là encore, le sens des flèches à son importance.
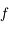
est négative dans le cas d'une lentille convergente et positive dans le cas d'une lentille divergente.
Crédit :
ASM/B. Mollier
Nous avons commencé à parler de distance négative et de grandeurs algébriques. Voici un petit aparté pour détailler ces notions.
 Excusez-moi m'dame, où est la boulangerie ?
Excusez-moi m'dame, où est la boulangerie ?
Dans la rue, quelqu'un vous demande où se situe la boulangerie la plus proche. Vous lui indiquez qu'elle est à 100 m. Oui, mais cette indication ne précise pas si elle est à 100 m devant ou derrière. Certes, en général, c'est implicite, ou accompagné d'un geste pour préciser la direction à emprunter. Cependant, en physique, il y a rarement quelqu'un pour nous indiquer le sens. Comment s'en sortir ? Si la boulangerie se situe devant nous, nous dirons effectivement qu'elle est à 100 m. Et si elle est derrière, qu'elle est à -100 m. C'est ce qu'on appelle des grandeurs algébriques. Il reste cependant encore un problème à régler. Si on se retourne, ce qui était devant devient derrière et inversement. Il faut en fait choisir un sens pour orienter nos mesures. Reprenons notre rue. Si elle est à sens unique, le plus simple est de choisir le sens de circulation des voitures pour orienter notre axe. Les distances dans le sens de circulation seront positives, et celle dans le sens opposé seront négatives.
Mesures algébriques
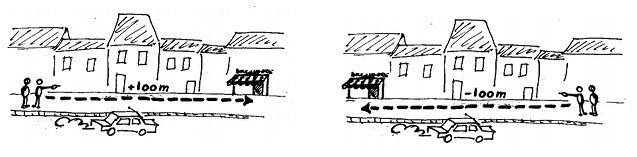
La boulangerie est située devant ? Elle est à + 100 m. Elle est située derrière ? Elle est à - 100 m.
Crédit :
B. Mollier
 Grandeurs algébriques en optique
Grandeurs algébriques en optique
En optique, ce sera pareil. Sauf que de circulation il n'est pas question. Mais nous prendrons pour orienter notre axe optique le sens de parcours des photons. Les distances orientées dans le même sens que l'axe optique seront comptées positivement (comme la distance focale image pour une lentille convergente), et celles dans le sens opposé seront comptées négativement (comme la distance focale objet pour une lentille convergente).
Considérons un faisceau parallèle mais arrivant avec une incidence non nulle par rapport à l'axe optique. Dans le cas de la lentille convergente, ils convergent en point appartenant nécessairement à l'axe 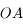 car tout rayon passant par le centre de la lentille n'est pas dévié. On s'aperçoit que ce point, que nous appellerons foyer secondaire image, est à la verticale du foyer principal image.
car tout rayon passant par le centre de la lentille n'est pas dévié. On s'aperçoit que ce point, que nous appellerons foyer secondaire image, est à la verticale du foyer principal image.
Exemple de foyer secondaire dans le cas d'un lentille convergente
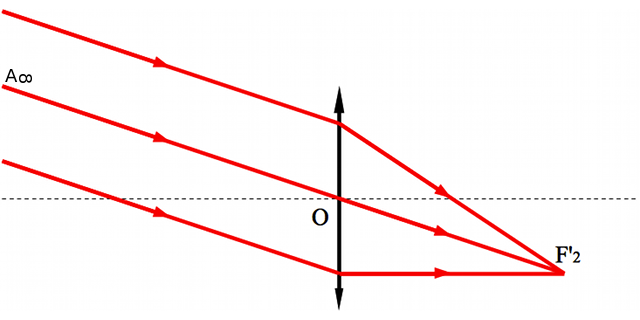
Crédit :
ASM/B. Mollier
Remarque : En fait, cette dernière remarque est vraie dans l'approximation de Gauss, qui garantit un aplanétisme approché.
Si l'inclinaison du faisceau varie, ce point (le foyer secondaire) parcourt ce que l'on nomme le plan focal de la lentille.
Pour une lentille divergente, on retrouve le même phénomène, sauf que les foyers secondaires images sont virtuels et situés en amont de la lentille. Comme précédemment, nous allons pouvoir définir un foyer secondaire objet, comme étant l'antécédent d'un point image situé à l'infini, en dehors de l'axe optique. L'ensemble des foyers secondaires objets constitueront le plan focal objet.
Exemple de foyer secondaire pour une lentille divergente
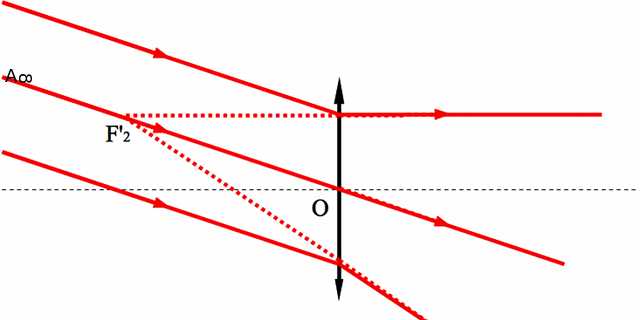
Crédit :
ASM/B. Mollier
Dans les conditions de Gauss, les plans focaux sont perpendiculaires à l'axe optique. Dans la vraie vie, ce sont des surfaces non planes. Les plaques photos utilisées au foyer d'un télescope de Schmidt étaient sphériques.
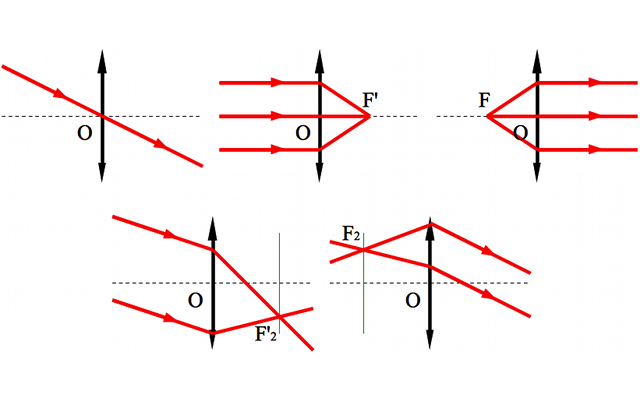
Munis de ces outils, nous allons pouvoir définir quelques propriétés sur les rayons lumineux traversant des lentilles. Elles vont nous permettre d'aborder, au paragraphe suivant, la construction des images.
- Tout rayon passant par le centre de la lentille n'est pas dévié.
- Tout rayon parallèle à l'axe optique converge au foyer principal image.
- Tout rayon passant par le foyer principal objet ressort parallèle à l'axe optique.
- Deux rayons parallèles entre eux se croisent dans le plan focal image.
- Deux rayons se croisant dans le plan focal objet ressortent parallèles entre eux.
Résumé
Crédit :
ASM/B. Mollier
 Remarques
Remarques
- L'image
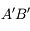 est inversée. On retrouve le deuxième cas décrit dans l'exemple décrit précédemment.
est inversée. On retrouve le deuxième cas décrit dans l'exemple décrit précédemment. - L'image
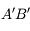 est réelle car en aval de la lentille.
est réelle car en aval de la lentille.
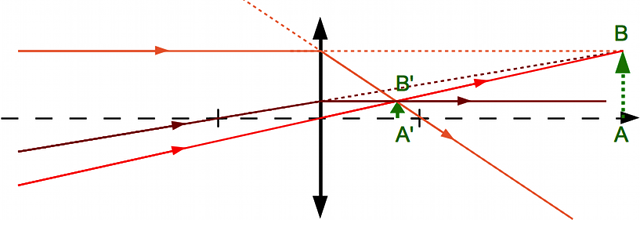
Continuons à faire avancer l'objet de telle manière qu'il passe de l'autre côté de la lentille. Il est dorénavant virtuel. Comment arriver à un tel résultat. Facile. En utilisant une deuxième lentille. On place un objet réel devant cette seconde lentille. Elle produit une image réelle. Plaçons la première lentille entre la seconde et l'image, et le tour est joué. Que nous donne le tracé cette fois-ci ?
Objet virtuel
Crédit :
ASM/B. Mollier
 On constate que
On constate que
 Remarque
Remarque
Remarquons tout de suite que la taille de l'image (sur un détecteur CCD par exemple) est tout simplement le produit du diamètre apparent (en radians) par la focale de l'instrument.
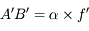
 Cas de la lentille divergente
Cas de la lentille divergente
Changeons de lentille pour passer aux lentilles divergentes. La différence par rapport aux cas précédents est que les positions des foyers objets et images sont inversées. Recommençons la procédure précédente.
 Objet virtuel à travers une lentille divergente
Objet virtuel à travers une lentille divergente
Bon, je pense que vous avez compris le principe. Je vous laisse les deux suivants en exercice.
Ne vous inquiétez pas, on ne va pas être obligé de systématiquement tracer toutes nos images dès qu'on voudra obtenir la moindre position ou taille. Il existe des relations simples, nommées relations de conjugaison, permettant d'accéder à toutes ces données, connaissant uniquement la distance focale de la lentille.
Nous allons les démontrer à partir des constructions précédentes.
Crédit :
B. Mollier
Nous avons vu que la taille de l'image n'est pas nécessairement la même que celle de l'objet. Et celle-ci varie en fonction de la distance de l'objet et de la distance focale.
 Grandissement
Grandissement
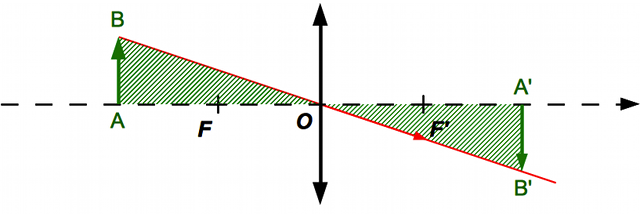
Nous allons appeler grandissement le rapport des tailles de l'objet et de l'image.
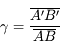
Crédit :
B. Mollier
En appliquant le théorème de Thalès, on trouve immédiatement que :
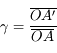
 Remarque
Remarque
Connaissant la distance de l'objet et de l'image, il est donc possible de calculer la taille de l'image.
Si le grandissement est positif, alors l'objet et l'image sont dans le même sens ; s'il est négatif, l'image est inversée par rapport à l'objet.
Si le grandissement est supérieur à 1, ou inférieur à -1, alors l'image est plus grande que l'objet. S'il est compris entre -1 et 1, l'image sera plus petite.
Auteur: B. Mollier
 Quelques grandissements
Quelques grandissements
Difficulté : ☆
Temps : 5 min
Voici 3 constructions géométriques :
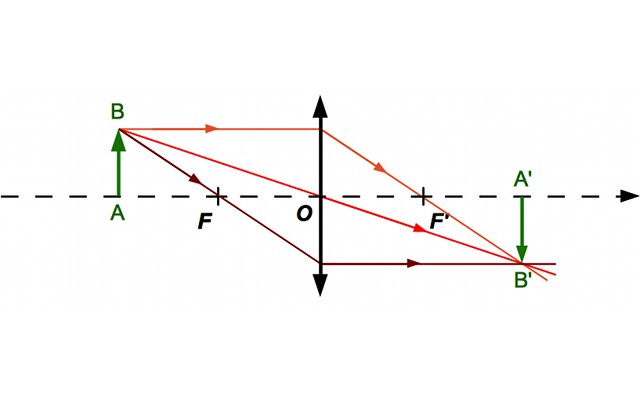
Construction 1
Crédit :
ASM/B. Mollier
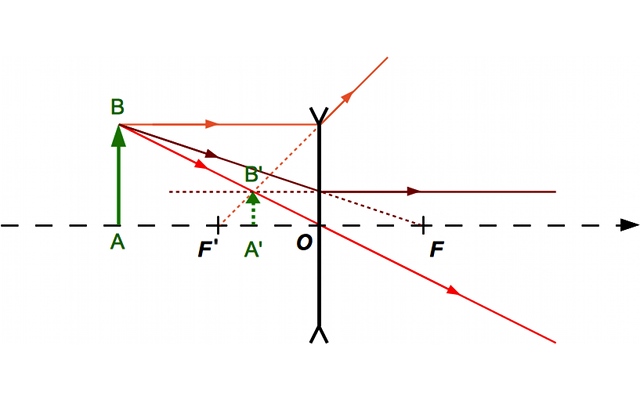
Construction 2
Crédit :
ASM/B. Mollier
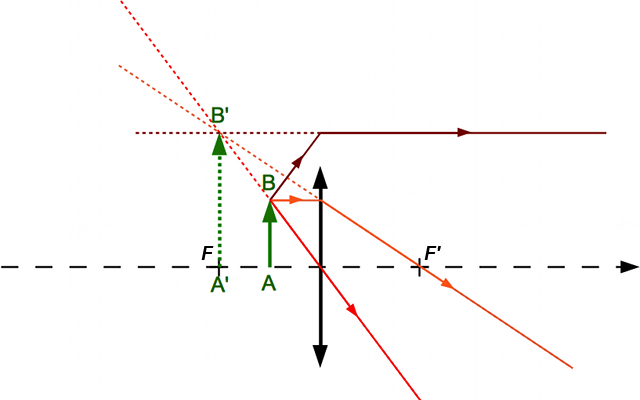
Construction 3
Crédit :
ASM/B. Mollier
Question 1)
Calculez le grandissement dans les trois cas.
Prenez les mesures sur les dessins.
 Grandissement : origines aux foyers
Grandissement : origines aux foyers
Et si on ne connaît pas la position de l'image ? Nous allons utiliser les foyers. En appliquant cette fois-ci le théorème de Thalès deux fois de chaque côté de la lentille, on obtient :
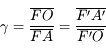
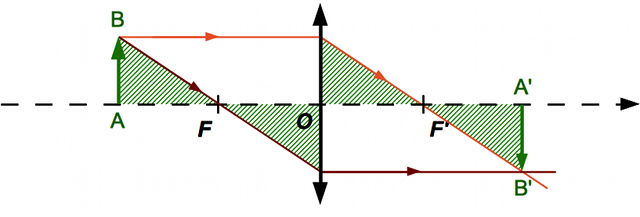
Crédit :
ASM/B. Mollier
Et voilà, connaissant la distance focale et la distance de l'objet, on peut calculer le grandissement.
 Relation de conjugaison de Newton (origines aux foyers)
Relation de conjugaison de Newton (origines aux foyers)
Remarquons qu'à partir de ces deux formules, on va pouvoir calculer la distance de l'image.
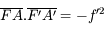
Nous venons d'établir la relation de conjugaison de Newton. Elle est aussi appelée relation de conjugaison avec origine au foyer, car les distances de l'objet et de l'image sont comptées à partir des foyers principaux.
Auteur: B. Mollier
 Quelques grandissements (2)
Quelques grandissements (2)
Difficulté : ☆
Temps : 5 min
On reprend les mêmes et on recommence !
Construction 1

Crédit :
ASM/B. Mollier
Construction 2

Crédit :
ASM/B. Mollier
Construction 3

Crédit :
ASM/B. Mollier
Question 1)
Sachant que la distance focale est de 4 cm en valeur absolue dans les 3 cas, retrouvez les valeurs de grandissement précédemment établies.
Pour ceux qui aurait la flemme de mesurer les distances 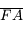 sur les figures,
sur les figures,
Auteur: B. Mollier
 Formule de Newton
Formule de Newton
On considère une lentille convergente de vergence 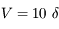 . On place un objet à une distance
. On place un objet à une distance 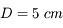 en amont du centre de la lentille.
en amont du centre de la lentille.
Question 1)
Calculez la position de l'image.
Calculez la distance focale image à partir de la vergence. Calculez la distance 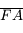 en appliquant la relation de Chasles. En déduire la position de l'image en appliquant la formule de Newton.
en appliquant la relation de Chasles. En déduire la position de l'image en appliquant la formule de Newton.
Question 2)
Est-elle réelle ou virtuelle ?
Question 3)
Calculez sa taille.
 Une autre relation de conjugaison
Une autre relation de conjugaison
Nous pouvons également obtenir une relation similaire, avec origine au centre de la lentille cette fois-ci. En partant de la formule du grandissement :
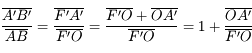
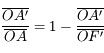
 Relation de conjugaison de Descartes (avec origine au centre)
Relation de conjugaison de Descartes (avec origine au centre)
On obtient ainsi la relation de conjugaison de Descartes :
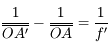
Auteur: B. Mollier
 Lunettes pour myope
Lunettes pour myope
Difficulté : ☆☆
Temps : 10 min
Considérons une paire de lunettes correctrices pour la myopie. L'ordonnance indique une vergence de 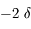 .
.

Crédit :
B. Mollier
Question 1)
Quelle est la distance focale image de la paire de lunettes ? Quelle est le type de lentilles utilisées ?
Question 2)
Muni de cette paire de lunettes, je lis un livre situé à 30 cm de mon visage. Quelle est la distance de l'image de cet ouvrage à travers les lunettes ?
Auteur: B. Mollier
 Condition de formation d'image
Condition de formation d'image
Difficulté : ☆☆☆
Temps : 20 min
On dispose d'un objet, d'un écran, et d'une lentille convergente de distance focale image 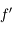 .
.
Question 1)
Quelle doit être la distance minimale 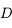 entre l'objet et l'écran pour pouvoir y former son image ?
entre l'objet et l'écran pour pouvoir y former son image ?
 Les lentilles
Les lentilles
Nous venons donc de voir qu'il existe deux types de lentilles minces : des lentilles convergentes, une loupe par exemple, qui ont la propriété de faire converger un faisceau lumineux ; des lentilles divergentes, comme des verres correcteurs de myopie, qui font diverger un faisceau lumineux.
 Éléments cardinaux
Éléments cardinaux
Nous avons défini trois points particuliers d'une lentille : le centre 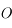 , centre de symétrie de celle-ci, par lequel aucun rayon lumineux n'est dévié ; le foyer principal image, image d'un point situé à l'infini sur l'axe optique ; le foyer principal objet, antécédent d'un point situé à l'infini sur l'axe optique. Ces points sont appelés éléments cardinaux de la lentille.
, centre de symétrie de celle-ci, par lequel aucun rayon lumineux n'est dévié ; le foyer principal image, image d'un point situé à l'infini sur l'axe optique ; le foyer principal objet, antécédent d'un point situé à l'infini sur l'axe optique. Ces points sont appelés éléments cardinaux de la lentille.
 Distance focale. Vergence
Distance focale. Vergence
Les distances entre ces points sont appelées distances focales. Ce sont des données de la lentille. Elles caractérisent la vergence de la lentille, c'est-à-dire son pouvoir de dévier les rayons lumineux.
 Tracés d'images
Tracés d'images
À l'aide de trois rayons, il nous est désormais possible de tracer l'image d'un objet à travers une lentille. Le rayon lumineux passant par le centre d'une lentille n'est pas dévié, celui arrivant parallèle à l'axe optique ressort en croisant le foyer principal image, et celui passant par le foyer principal objet ressortira de la lentille parallèle à l'axe optique.
 Relations de conjugaison
Relations de conjugaison
Enfin, nous avons quelques relations qui nous permettront de calculer des tailles d'images, les distances où elles se forment et pourquoi pas des champs de vue et des grossissements. Ce sera pour bientôt.

Crédit :
B. Mollier



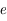 est petite devant le rayon de courbure des dioptres et devant la distance entre les centres
est petite devant le rayon de courbure des dioptres et devant la distance entre les centres  et
et  .
.




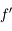 . C'est une quantité algébrique, c'est-à-dire qu'on la compte positivement dans le sens de propagation de la lumière.
. C'est une quantité algébrique, c'est-à-dire qu'on la compte positivement dans le sens de propagation de la lumière. 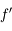 est positif dans le cas d'une lentille convergente et négatif dans le cas d'une divergente.
est positif dans le cas d'une lentille convergente et négatif dans le cas d'une divergente.

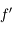 comme étant la distance du centre
comme étant la distance du centre 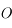 de la lentille au foyer principal image
de la lentille au foyer principal image 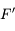 . Notez le sens de la flèche. Dans le cas d'une lentille convergente, elle est dans le même sens que celui de la propagation de la lumière. Cette distance est alors positive. Dans le cas de la lentille divergente, cette flèche est dans le sens opposé à la propagation de la lumière. Cette distance est alors comptée négativement. Pour plus d'information sur ces notions de distances positives et négatives, lisez cette
. Notez le sens de la flèche. Dans le cas d'une lentille convergente, elle est dans le même sens que celui de la propagation de la lumière. Cette distance est alors positive. Dans le cas de la lentille divergente, cette flèche est dans le sens opposé à la propagation de la lumière. Cette distance est alors comptée négativement. Pour plus d'information sur ces notions de distances positives et négatives, lisez cette 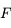 et
et 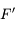 étant symétriques par rapport au centre
étant symétriques par rapport au centre 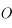 , on obtient
, on obtient 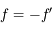 .
.

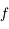 comme étant la distance séparant le centre de la lentille et le foyer principal objet. Là encore, le sens des flèches à son importance.
comme étant la distance séparant le centre de la lentille et le foyer principal objet. Là encore, le sens des flèches à son importance. 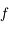 est négative dans le cas d'une lentille convergente et positive dans le cas d'une lentille divergente.
est négative dans le cas d'une lentille convergente et positive dans le cas d'une lentille divergente.
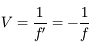
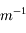 ou encore en dioptrie (noté
ou encore en dioptrie (noté 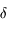 ). Par exemple, une lentille divergente de distance focale
). Par exemple, une lentille divergente de distance focale 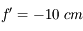 (correction pour une myopie sévère) possède une vergence de
(correction pour une myopie sévère) possède une vergence de 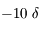 . C'est le nombre annoncé dans les ordonnances pour les lunettes.
. C'est le nombre annoncé dans les ordonnances pour les lunettes.

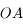 car tout rayon passant par le centre de la lentille n'est pas dévié. On s'aperçoit que ce point, que nous appellerons foyer secondaire image, est à la verticale du foyer principal image.
car tout rayon passant par le centre de la lentille n'est pas dévié. On s'aperçoit que ce point, que nous appellerons foyer secondaire image, est à la verticale du foyer principal image.



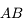 en amont de la lentille et du foyer objet. On cherche à tracer son image à travers la lentille.
en amont de la lentille et du foyer objet. On cherche à tracer son image à travers la lentille.
 et passant par
et passant par 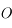 . Il n'est pas dévié.
. Il n'est pas dévié.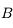 . En effet, dans les conditions de stigmatisme approché, deux rayons suffisent à définir un point image. On a le choix entre deux autres rayons. On trace par exemple le rayon issu de
. En effet, dans les conditions de stigmatisme approché, deux rayons suffisent à définir un point image. On a le choix entre deux autres rayons. On trace par exemple le rayon issu de 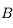 et parallèle à l'axe optique. Il ressort de la lentille en passant par le foyer principal image
et parallèle à l'axe optique. Il ressort de la lentille en passant par le foyer principal image 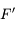 . Il croise le premier rayon en
. Il croise le premier rayon en 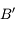 , image de
, image de 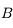 par la lentille.
par la lentille.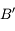 . Traçons le rayon issu de
. Traçons le rayon issu de 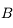 et passant par le foyer principal objet
et passant par le foyer principal objet 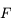 . Il ressort parallèle à l'axe optique. On vérifie ainsi qu'il passe effectivement par le point
. Il ressort parallèle à l'axe optique. On vérifie ainsi qu'il passe effectivement par le point 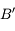 .
.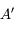 du point
du point 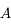 . On ne peut utiliser la même méthode que le point
. On ne peut utiliser la même méthode que le point 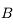 car tous ces rayons sont identiques et confondus avec l'axe optique. Comment s'en sortir alors ? Utilisons la propriété d'aplanétisme. On sait que
car tous ces rayons sont identiques et confondus avec l'axe optique. Comment s'en sortir alors ? Utilisons la propriété d'aplanétisme. On sait que 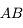 est perpendiculaire à l'axe optique. L'image
est perpendiculaire à l'axe optique. L'image 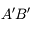 l'est également.
l'est également. 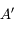 est donc le point de l'axe optique à la verticale de
est donc le point de l'axe optique à la verticale de 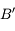 . Le tour est joué.
. Le tour est joué.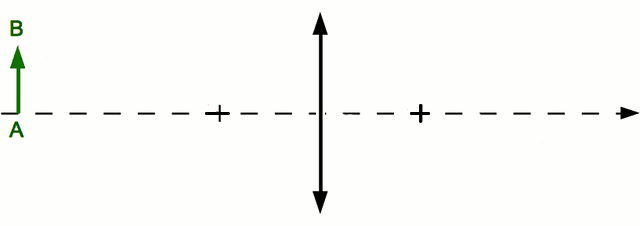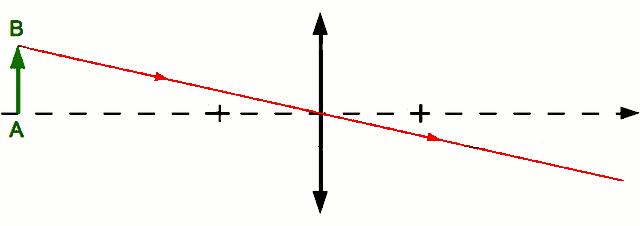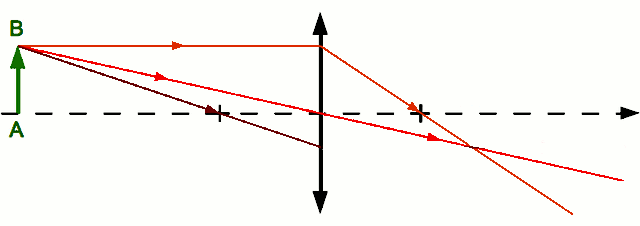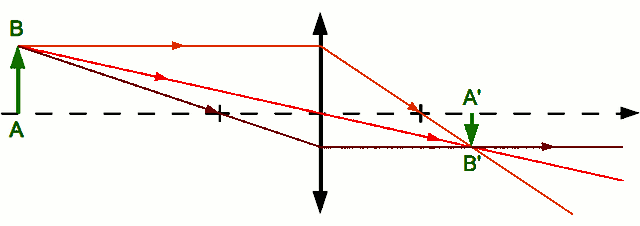
 est inversée. On retrouve le deuxième cas décrit dans l'exemple décrit
est inversée. On retrouve le deuxième cas décrit dans l'exemple décrit  est réelle car en aval de la lentille.
est réelle car en aval de la lentille.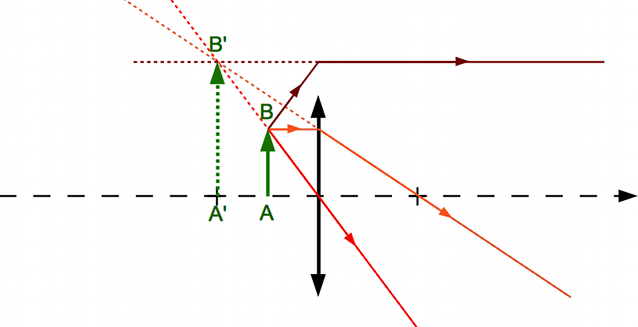
 est dans le même sens.
est dans le même sens. est virtuelle car en amont de la lentille.
est virtuelle car en amont de la lentille.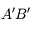 est plus grande que l'objet. On a affaire à une loupe.
est plus grande que l'objet. On a affaire à une loupe.
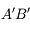 est :
est :
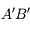 est :
est :
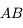 à l'infini. Il possédera un diamètre apparent
à l'infini. Il possédera un diamètre apparent 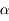 .
.
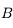 et passant par
et passant par 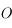 . Il n'est pas dévié.
. Il n'est pas dévié.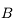 sont parallèles les uns aux autres. Nous pouvons cependant tracer le rayon parallèle au premier passant par le foyer objet. Il ressortira parallèle à l'axe optique. On constate qu'il coupe le premier dans le plan focal. C'est normal. Nous avons défini le plan focal image comme ceci.
sont parallèles les uns aux autres. Nous pouvons cependant tracer le rayon parallèle au premier passant par le foyer objet. Il ressortira parallèle à l'axe optique. On constate qu'il coupe le premier dans le plan focal. C'est normal. Nous avons défini le plan focal image comme ceci.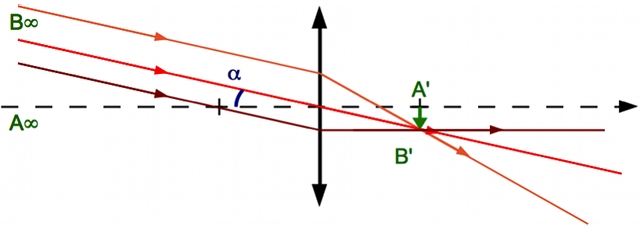
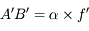
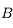 et passant par
et passant par 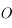 . Il n'est toujours pas dévié.
. Il n'est toujours pas dévié.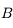 et parallèle à l'axe optique. Il ressort de la lentille en passant par le foyer principal image
et parallèle à l'axe optique. Il ressort de la lentille en passant par le foyer principal image 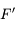 . Mais ce foyer est en amont de la lentille.
. Mais ce foyer est en amont de la lentille.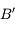 . Traçons le rayon issu de
. Traçons le rayon issu de 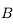 et passant par le foyer principal objet
et passant par le foyer principal objet 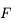 . Il ressort parallèle à l'axe optique. On vérifie ainsi qu'il passe effectivement par le point
. Il ressort parallèle à l'axe optique. On vérifie ainsi qu'il passe effectivement par le point 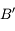
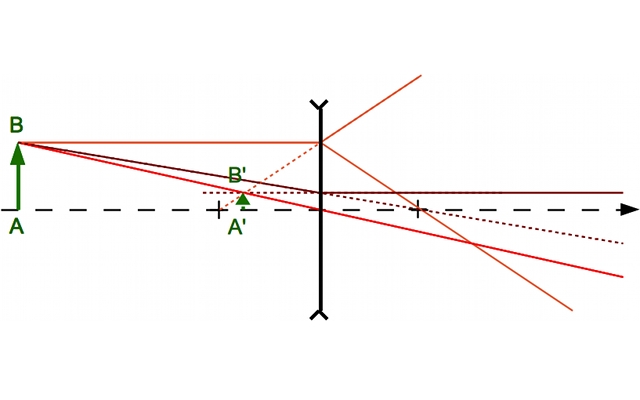
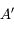 du point
du point 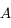 . On ne peut utiliser la même méthode que le point
. On ne peut utiliser la même méthode que le point 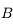 car tous ces rayons sont identiques et confondus avec l'axe optique. Comment s'en sortir alors. Utilisons la propriété d'aplanétisme. On sait que
car tous ces rayons sont identiques et confondus avec l'axe optique. Comment s'en sortir alors. Utilisons la propriété d'aplanétisme. On sait que 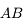 est perpendiculaire à l'axe optique. L'image
est perpendiculaire à l'axe optique. L'image 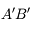 l'est également.
l'est également. 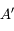 est donc le point de l'axe optique à la verticale de
est donc le point de l'axe optique à la verticale de 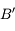 .
.
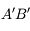 est :
est :
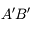 est :
est :
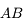 et d'une lentille divergente. Trouvez le tracé correct.
et d'une lentille divergente. Trouvez le tracé correct.

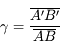

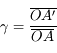



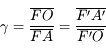

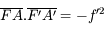
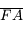 sur les figures,
sur les figures,
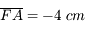
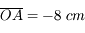
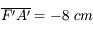
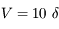 . On place un objet à une distance
. On place un objet à une distance 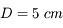 en amont du centre de la lentille.
en amont du centre de la lentille.
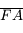 en appliquant la relation de Chasles. En déduire la position de l'image en appliquant la formule de Newton.
en appliquant la relation de Chasles. En déduire la position de l'image en appliquant la formule de Newton.
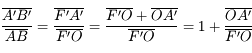
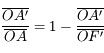
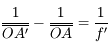
 et
et 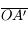 respectivement
respectivement 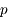 et
et 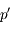 .
.
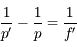
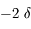 .
.

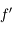 .
.
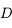 entre l'objet et l'écran pour pouvoir y former son image ?
entre l'objet et l'écran pour pouvoir y former son image ?
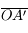 en fonction de
en fonction de 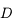 et
et 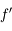 . Déduisez-en une condition sur
. Déduisez-en une condition sur 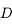 pour que l'image existe.
pour que l'image existe.
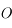 , centre de symétrie de celle-ci, par lequel aucun rayon lumineux n'est dévié ; le foyer principal image, image d'un point situé à l'infini sur l'axe optique ; le foyer principal objet, antécédent d'un point situé à l'infini sur l'axe optique. Ces points sont appelés éléments cardinaux de la lentille.
, centre de symétrie de celle-ci, par lequel aucun rayon lumineux n'est dévié ; le foyer principal image, image d'un point situé à l'infini sur l'axe optique ; le foyer principal objet, antécédent d'un point situé à l'infini sur l'axe optique. Ces points sont appelés éléments cardinaux de la lentille.
 , l'image et l'objet font la même taille mais sont inversés l'un par rapport à l'autre.
, l'image et l'objet font la même taille mais sont inversés l'un par rapport à l'autre. , l'image est 3 fois plus petite et dans le même sens que l'objet.
, l'image est 3 fois plus petite et dans le même sens que l'objet. , l'image est 2 fois plus grande et dans le même sens que l'objet.
, l'image est 2 fois plus grande et dans le même sens que l'objet. , l'image et l'objet font la même taille mais sont inversés l'un par rapport à l'autre.
, l'image et l'objet font la même taille mais sont inversés l'un par rapport à l'autre. , l'image est 3 fois plus petite et dans le même sens que l'objet.
, l'image est 3 fois plus petite et dans le même sens que l'objet. , l'image est 2 fois plus grande et dans le même sens que l'objet.
, l'image est 2 fois plus grande et dans le même sens que l'objet. vaut
vaut  .
.
 .
.




 . Cette distance est négative, il s'agit donc de lentilles divergentes.
. Cette distance est négative, il s'agit donc de lentilles divergentes.
 .
.
 d'où
d'où 

 .
.

 en fonction de
en fonction de  et
et 



 . Si la distance entre l'objet et l'écran est inférieure à 4 fois la distance focale, il sera impossible de faire apparaître l'image sur l'écran !
. Si la distance entre l'objet et l'écran est inférieure à 4 fois la distance focale, il sera impossible de faire apparaître l'image sur l'écran !