Bruit de Poisson

Introduction

Cette démonstration simule le comportement d'une variable aléatoire entière suivant la loi de Poisson. Typiquement, il s'agit du nombre d'événements poissonien survenant pendant un temps fixe donné à l'avance. Ce peut être le nombre de photons arrivant sur un détecteur pendant une unité de temps.

Une variable aléatoire de Poisson est caractérisée part un seul nombre qui est à la fois la moyenne du nombre d'événements arrivant dans le temps considéré et la variance de ce nombre. Si T désigne le temps que dure l'observation, on a = 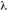T où 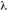désigne le taux moyen d'arrivée des événements ( en nombre d'événements par seconde par exemple. )

La loi de Poisson est souvent appelée la "loi des événements rares" car elle peut s'obtenir comme cas limite de la loi binomiale lorsque la probabilité de succès est faible devant le nombre d'épreuves.

Liste des paramètres de l'applet

• label : mu
  type : nombre
  titre : nombre moyen d'événements dans le temps T
  unités : sans dimension
  Le premier champ désigne le nombre moyen d'événements dans le temps donné T. Par défaut cette valeur est mise à 5, on peut garder cette valeur dans un premier temps.
• label : npts
  type : nombre
  titre : nombre d'expériences successives
  unités : nombre sans dimension
  Le deuxième champ est la taille de l'échantillon de Poisson. Par défaut on procède à 30 expériences qui sont autant d'observations de la variable aléatoire de Poisson.

Mode d'emploi de l'applet

1. Le bouton "Bruit de Poisson" lance une simulation d'un échantillon poissonien de la taille sélectionnée. Le bouton "Relancer" permet de passer à l'échantillon suivant.
2. Le bouton "Moyenne" illustre la loi des grands nombres. Une série de simulations est lancée et en même temps la moyenne arithmétique de ces simulations est calculée. L'échantillon est en rouge et la moyenne arithmétique est en bleu. Cette simulation est sans fin, il faut l'arrêter avec le bouton "Stop".
3. Le bouton "Tableau" présente l'échantillon de Poisson suivant un tableau à deux colonnes. La colonne de gauche "sx" est le rang de la variable de Poisson dans l'échantillon et la colonne de droite "sy" est la valeur prise par la variable de Poisson.

Exemple d'utilisation

Dans ce premier exemple on laisse les paramètres à leurs valeurs par défaut c'est-à-dire 5 pour la moyenne et 30 pour la taille de l'échantillon. On clique ensuite sur le bouton "bruit de Poisson" pour obtenir un échantillon de 30 réalisations indépendantes d'une variable de Poisson de moyenne 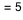, ces réalisations sont figurées par une barre rouge dont la hauteur est le nombre obtenu, il s'agit toujours d'un entier positif.

Exemple d'utilisation

Dans notre cas la loi des grands nombres dit que la moyenne arithmétique de 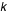variables de Poisson indépendantes converge vers leur moyenne commune . Pour le voir, gardez les valeurs par défaut et lancez l'application en cliquant sur "moyenne". On voit alors une animation où les barres rouges représentent les échantillons de Poisson successifs et les barres bleues la moyenne arithmétique des échantillons. On constate que les fluctuations des barres rouges restent constantes alors que celles des barres bleues semblent s'amortir avec le temps et converger vers une droite de valeur (qui devrait être restée à cinq si vous avez laissé les valeurs par défaut). Les barres rouges et bleues sont décalées pour plus de visibilité. L'animation est limité à 400 itérations, laissez-la se dérouler cent fois environ et arrêtez-la avec le bouton "stop".

On constate alors que les barres bleues (les moyennes arithmétiques) fluctuent beaucoup moins que l'échantillon lui-même autour de . Les moyennes arithmétiques sont des variables aléatoires, ce ne sont pas des variables aléatoires de Poisson, elles possèdent la moyenne mais leur variance n'est pas elle est égale à / 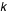où 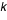est le nombre de variables dont on fait la moyenne arithmétique. La meilleure qualité de l'échantillon bleu par rapport à une réalisation rouge s'exprime à l'aide du rapport signal-sur-bruit noté : 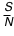. Ce rapport n'a de sens que pour des variables positives, il est égal au quotient de la moyenne divisé par l'écart type (l'écart type est la racine carré de la variance) il vaut 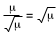pour l'échantillon rouge et 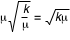pour la moyenne arithmétique. Ainsi lorsque le nombre d'échantillons augmente, le rapport signal-sur-bruit de leur moyenne arithmétique augmente aussi, le signal converge vers la moyenne le rapport signal-sur-bruit permet de quantifier la qualité de l'approximation de la moyenne par la moyenne arithmétique.