Fonction de répartition d'une loi de Poisson
Date de création : 12/01/2004
Auteur: Didier Pelat
Introduction
Cette démonstration est assez semblable dans ces objectifs à celle sur les histogrammes mais elle introduit un outil beaucoup plus pratique que l'histogramme : la fonction de répartition.
On introduit la fonction de répartition théorique et la fonction de répartition empirique.
La fonction de répartition d'une variable aléatoire est la probabilité pour que cette variable ne dépasse pas un certain seuil 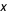 , ou ce qui revient au même, pour quelle soit inférieure ou égale à 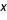 .
Si 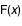 désigne la fonction de répartition de la variable aléatoire 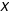 on a par définition :  .
La fonction de répartition empirique correspond à la proportion des valeurs de l'échantillon où le niveau 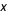 n'a pas été dépassé.
Elle est donc égale au nombre de fois où la valeur de l'échantillon est inférieure ou égale à 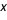 divisé par la taille de l'échantillon.
L'avantage de la fonction de répartition empirique sur l'histogramme, c'est que sa définition est la même pour les variables discrètes et continues, il n'y a pas de problème de classes.
Cette démonstration illustre, pour la loi de Poisson, un résultat important de probabilité qui dit que la fonction de répartition empirique converge presque-sûrement et uniformément vers la fonction de répartition théorique.
Ce résultat est connu sous le nom de théorème de Glivenko-Cantelli.
Liste des paramètres de l'applet
-
label : mu
type : nombre
titre : moyenne de la loi de Poisson
unités : sans dimensions
Cette case permet de préciser la moyenne de la variable de Poisson que l'on désire étudier par défaut elle vaut cinq.
-
label : npts
type : nombre
titre : taille de l'échantillon dont on calcule la fonction de répartition empirique
unités : nombre entier positif
Ici on précise la taille de l'échantillon, il vaut trente par défaut.
-
label : tcl
type : string
titre : affiche ou non la loi de Gauss de même moyenne et de même écart type
Cette case à cocher permet de visualiser la fonction de répartition de l'approximation gaussienne.
Dans un premier temps, il est recommandé de laisser cette case décochée.
Mode d'emploi de l'applet
La démonstration est lancée à l'aide de deux boutons :
- Le bouton "bruit de Poisson-fct de répartition" affiche en rouge la fonction de répartition empirique obtenu à l'aide de l'échantillon de la taille sélectionnée (30 si on a laissé les valeurs par défaut).
- Le bouton "moyenne" montre la convergence de la moyenne arithmétique des fonctions de répartitions empiriques vers la fonction de répartition théorique.
Exemple d'utilisation
Cet exemple va nous permettre de nous familiariser avec la forme d'une fonction de répartition empirique d'une variable de Poisson.
On lance la démonstration en cliquant sur le bouton "bruit de Poisson-fct de répartition".
Il est recommandé de décocher la case "Gauss limit" et de laisser les valeurs par défaut.
La fonction de répartition théorique est en bleu, c'est une fonction en escalier non décroissante comme il se doit pour les variables aléatoires discrètes.
La fonction de répartition empirique est en rouge, c'est toujours une fonction en escalier, que la variable soit discrète ou continue.
Normalement cette fonction est discontinue pour les valeurs observées et les traits verticaux ne devraient pas figurer.
On les a cependant tracés ici ce qui permet, pour la fonction empirique, de visualiser à l'aide de petit traits horizontaux le nombre de fois où la valeur a été observée.
On peut obtenir d'autres histogrammes empiriques en cliquant sur la case "Relancer".
Exemple d'utilisation
Cette démonstration illustre le très important théorème de Glivenko-Cantelli évoqué plus haut.
On revient au début de la démonstration en cliquant, si nécessaire, sur la barre "Réinitialiser".
On laisse 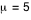 et "sample size" à 30 et on clique sur le bouton "convergence".
Pour arrêter la démonstration il faut cliquer sur "stop".
L'animation montre la fonction de répartition empirique lorsque la taille de l'échantillon augmente à partir de 1.
On constate qu'au fur et à mesure que la taille de l'échantillon augmente, la courbe empirique rouge se rapproche de la courbe théorique bleue au sens que leur différence verticale (la distance de Kolmogoroff) diminue en moyenne quand la taille de l'échantillon augmente.
Il ne faut pas oublier qu'il s'agit d'une convergence stochastique et que de grandes fluctuations restent possibles.
|