On lance l'animation en cliquant sur le bouton "TCL". On constate alors qu'effectivement la courbe rouge se rapproche de plus en plus de la courbe bleue. On mesure l'écart entre les deux courbes à l'aide d'un nombre égal à leur plus grande séparation verticale. Ce nombre est la distance de Kolmogoroff entre les deux courbes, c'est effectivement une distance au sens mathématique du terme. Ce que l'on voit, c'est que lorsque la moyenne d'une loi de Poisson augmente, alors la fonction de répartition de la variable réduite se rapproche au sens de la distance de Kolmogoroff de la fonction de répartition d'une loi normale réduite (c'est-à-dire d'une loi normale de moyenne nulle et d'écart type unité). On dit que la variable aléatoire de Poisson réduite converge en loi vers une variable aléatoire normale réduite lorsque tend vers l'infini.

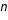
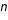
La convergence en loi d'une variable de Poisson réduite vers une variable normale réduite est prévue par le Théorème central limite. Ce théorème dit, dans une de ces nombreuses versions, que la somme de variables aléatoires identiques et indépendantes converge en loi vers la loi normale lorsque tend vers l'infini à condition que les variables dont on fait la somme possèdent une moyenne et une variance (ou un écart type). Le théorème s'applique en effet car une variable aléatoire de Poisson de moyenne entière (ce qui est le cas ici) est la somme de lois de Poisson indépendantes de moyenne unité et donc de variance unité aussi. On trouvera une autre illustration de ce théorème, mais pour des variables continues, avec l'animation "TCL2".
Remarque : L'expression Théorème central limite veut dire "Théorème établissant une limite dont l'importance est centrale", c'est la traduction mot-à-mot d'une expression allemande. Ce qui est central c'est le théorème pas la limite, et l'expression, parfois rencontrée, de "Théorème de la limite centrée" est fautive.