Simulation: Onde d'Alfven
Auteur:
Roch Smets
Date de création: 06/05/2002
Date de mise à jour: 13/06/2002
Introduction:
Cette appliquette permet de visualiser la propagation d'une onde d'Alfvèn
dans un plasma magnétisé uniforme. Pour rendre le système le plus
simlple possible, la géométrie est supposée à une dimension. Il y a une
seule variable dans le système ;
 . Les vecteurs gardent cependant leurs 3 composantes. Pour pouvoir faire de tels calculs, il faut commencer par écrire les équations de la
MHD
qui gouvernent l'évolution du système. Ensuite, avant d'intégrer
numériquement ces équations, il faut les réécrire sans dimensions
. Ensuite se pose le choix de l'algorithme qui va permettre d'integrer ce
système correctement. Pour le système MHD idéal, l'algorithme de
Lax-Wendroff
est simple et bien adapté. Les conditions aux limites du code
étant périodiques, les grandeurs physiques ont la même valeur
aux deux extrémités. Avant de faire tourner l'appliquette, il ne
reste plus qu'à initialiser les paramètres d'entrée de l'appliquette
:
. Les vecteurs gardent cependant leurs 3 composantes. Pour pouvoir faire de tels calculs, il faut commencer par écrire les équations de la
MHD
qui gouvernent l'évolution du système. Ensuite, avant d'intégrer
numériquement ces équations, il faut les réécrire sans dimensions
. Ensuite se pose le choix de l'algorithme qui va permettre d'integrer ce
système correctement. Pour le système MHD idéal, l'algorithme de
Lax-Wendroff
est simple et bien adapté. Les conditions aux limites du code
étant périodiques, les grandeurs physiques ont la même valeur
aux deux extrémités. Avant de faire tourner l'appliquette, il ne
reste plus qu'à initialiser les paramètres d'entrée de l'appliquette
:
L'appliquette est disponible en suivant ce lien.
Retour au menu des appliquettes.
Liste des paramètres de l'appliquette:
-
label: b0
type: nombre
titre: magnitude B
unités: normalise
mode d'acquisition: champ
Intensite du champ magnétique statique qui règne dans le milieu.
-
label: n0
type: nombre
titre: densité
unités: normalise
mode d'acquisition: champ
Densité initiale
-
label: p0
type: nombre
titre: pression cinetique
unités: normalise
mode d'acquisition: champ
Pression cinétique initiale
-
label: kx
type: nombre
titre: nombre d'onde
unités: normalise
mode d'acquisition: choix
Nombre d'onde : il represente le nombre de longueurs d'onde présentes dans la boîte de simulation
-
label: am
type: nombre
titre: amplitude
unités: normalise
mode d'acquisition: champ
Amplitude de la perturbation magnétique dans la direction
y
-
label: th
type: nombre
titre: theta entre B et k
unités: degrés
mode d'acquisition: champ
Angle entre le champ magnétique compris dans le plan
xz et le vecteur d'onde dans la direction x
-
label: tm
type: nombre
titre: temps de la simulation
unités: normalise
mode d'acquisition: champ
Temps total de la simulation
Les autres paramètres de la simulation sont fixés
: la longueur de la boite est égale à 1, le pas de
grille est égale à 0.01 et le pas de temps est égale
à 0.005.
Equations MHD à 1 dimension
Comme cela a été présenté, un système MHD
se compose de plusieurs équations : les équations
constitutives du plasma et les équations du champ
électromagnétique (équations de Maxwell). La
résolution d'un tel système nécessite de résoudre
toute ces équations en même temps dans la
mesure ou elles sont couplées. Cette résolution
peut se faire numériquement sous certaines
conditions. Il faut pour cela utiliser un schéma
numérique qui permette d'intégrer ces équations
correctement. Un des schémas le plus simple et
le plus étudié est le schéma de Lax-Wendroff.
Il permet d'intégrer les équations aux dérivées
partielles de la forme
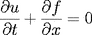
où
 et
et
 sont des vecteurs dépendant de la position et du
temps (cette forme particulière s'appelle encore
forme conservative des équations). Pour simplifier
le problème, on se place dans le cas à une dimension.
Les gradients n'ont donc plus qu'une composante
dans une direction que l'on nommera
sont des vecteurs dépendant de la position et du
temps (cette forme particulière s'appelle encore
forme conservative des équations). Pour simplifier
le problème, on se place dans le cas à une dimension.
Les gradients n'ont donc plus qu'une composante
dans une direction que l'on nommera
 . Pour les équations MHD, on arrive alors simplement
après un peu d'algèbre au système
. Pour les équations MHD, on arrive alors simplement
après un peu d'algèbre au système
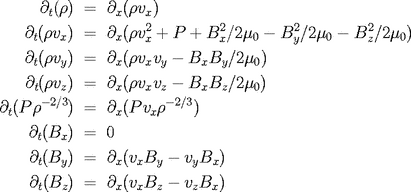
L'équation sur
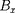 donne simplement que cette composante est
constante. Il reste donc à intégrer un système de
7 équations à 7 inconnues pour lequel on a
explicitement les composantes du vecteur u et
f.
donne simplement que cette composante est
constante. Il reste donc à intégrer un système de
7 équations à 7 inconnues pour lequel on a
explicitement les composantes du vecteur u et
f.
Equations sans dimension
De manière générale en simulation numérique,
pour éviter les erreurs d'arrondis et pour ne
pas travailler sur des nombres trop grand ou
trop petits, on récrit le système en fonction
de variables sans dimensions. La densité est
alors normalisée à la valeur de la densité
initiale (uniforme), le champ magnétique au
champ statique uniforme initiale, les vitesses
sont normalisées à la vitesse d'Alfvèn associée,
la longueur est normalisé à une longueur
caractéristique - la longueur de la boite de
simulation - et la pression est normalisée à la
pression initiale uniforme.
Algorithme de Lax-Wendroff
La résolution numérique d'une équation nécessite
d'utiliser une grille aussi bien en espace qu'en
temps : ainsi, les valeurs des champs
 et
et
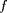 intervenant dans l'équation conservative ne seront
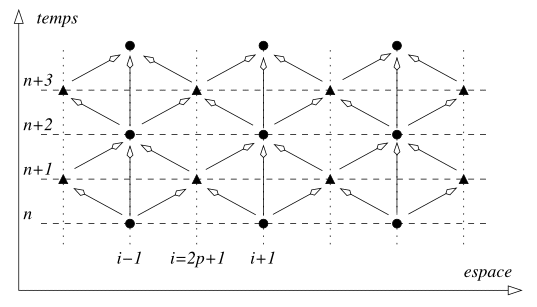
connues que sur ces points grilles. L'algorithme de
Lax-Wendroff est un algorithme de type saute-mouton
(leap-frog) qui utilise deux grilles décallées en espace
et en temps.
intervenant dans l'équation conservative ne seront
connues que sur ces points grilles. L'algorithme de
Lax-Wendroff est un algorithme de type saute-mouton
(leap-frog) qui utilise deux grilles décallées en espace
et en temps.
Si l'on connait à l'instant
 pair la valeur des champs
pair la valeur des champs
 et
et
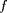 sur les points de grille pairs (indiqués par des
cercles sur le schema), on en déduit les valeurs
de
sur les points de grille pairs (indiqués par des
cercles sur le schema), on en déduit les valeurs
de
 (et donc de
(et donc de
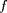 ) à l'instant
) à l'instant
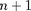 impair sur les points de grille impair (indiqués par des
triangles) avec
impair sur les points de grille impair (indiqués par des
triangles) avec
![n+1 n n n n u i = (1/2)[u i+1+u i- 1]- (Dt/2Dx)[f i+1 - f i- 1]](images-TeX4ht/mhd19x.gif)
On construit ensuite les valeurs de
 à l'instant
à l'instant
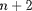 pair sur les points de grille pairs avec
pair sur les points de grille pairs avec
![n+2 n n+1 n+1 u i = u i- (Dt/Dx)[f i+1 - fi- 1 ]](images-TeX4ht/mhd22x.gif)
Avec cette méthode, la valeur du vecteur
 qui nous interesse ne sera connue qu'aux instants
qui nous interesse ne sera connue qu'aux instants
 pairs sur les points grille
pairs sur les points grille
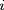 pairs, et que la grille des indices spatiaux et
temporelles impairs ne sert qu'à des calculs
intermédiaires.
pairs, et que la grille des indices spatiaux et
temporelles impairs ne sert qu'à des calculs
intermédiaires.
 . Les vecteurs gardent cependant leurs 3 composantes. Pour pouvoir faire de tels calculs, il faut commencer par écrire les équations de la
MHD
qui gouvernent l'évolution du système. Ensuite, avant d'intégrer
numériquement ces équations, il faut les réécrire sans dimensions
. Ensuite se pose le choix de l'algorithme qui va permettre d'integrer ce
système correctement. Pour le système MHD idéal, l'algorithme de
Lax-Wendroff
est simple et bien adapté. Les conditions aux limites du code
étant périodiques, les grandeurs physiques ont la même valeur
aux deux extrémités. Avant de faire tourner l'appliquette, il ne
reste plus qu'à initialiser les paramètres d'entrée de l'appliquette
:
. Les vecteurs gardent cependant leurs 3 composantes. Pour pouvoir faire de tels calculs, il faut commencer par écrire les équations de la
MHD
qui gouvernent l'évolution du système. Ensuite, avant d'intégrer
numériquement ces équations, il faut les réécrire sans dimensions
. Ensuite se pose le choix de l'algorithme qui va permettre d'integrer ce
système correctement. Pour le système MHD idéal, l'algorithme de
Lax-Wendroff
est simple et bien adapté. Les conditions aux limites du code
étant périodiques, les grandeurs physiques ont la même valeur
aux deux extrémités. Avant de faire tourner l'appliquette, il ne
reste plus qu'à initialiser les paramètres d'entrée de l'appliquette
: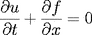
 et
et
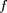 sont des vecteurs dépendant de la position et du
temps (cette forme particulière s'appelle encore
forme conservative des équations). Pour simplifier
le problème, on se place dans le cas à une dimension.
Les gradients n'ont donc plus qu'une composante
dans une direction que l'on nommera
sont des vecteurs dépendant de la position et du
temps (cette forme particulière s'appelle encore
forme conservative des équations). Pour simplifier
le problème, on se place dans le cas à une dimension.
Les gradients n'ont donc plus qu'une composante
dans une direction que l'on nommera
 . Pour les équations MHD, on arrive alors simplement
après un peu d'algèbre au système
. Pour les équations MHD, on arrive alors simplement
après un peu d'algèbre au système
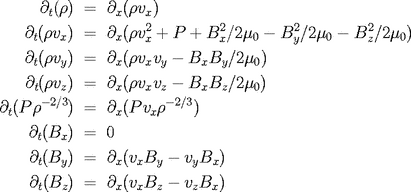
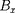 donne simplement que cette composante est
constante. Il reste donc à intégrer un système de
7 équations à 7 inconnues pour lequel on a
explicitement les composantes du vecteur u et
f.
donne simplement que cette composante est
constante. Il reste donc à intégrer un système de
7 équations à 7 inconnues pour lequel on a
explicitement les composantes du vecteur u et
f.
 et
et
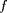 intervenant dans l'équation conservative ne seront
connues que sur ces points grilles. L'algorithme de
Lax-Wendroff est un algorithme de type saute-mouton
(leap-frog) qui utilise deux grilles décallées en espace
et en temps.
intervenant dans l'équation conservative ne seront
connues que sur ces points grilles. L'algorithme de
Lax-Wendroff est un algorithme de type saute-mouton
(leap-frog) qui utilise deux grilles décallées en espace
et en temps.

 pair la valeur des champs
pair la valeur des champs
 et
et
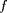 sur les points de grille pairs (indiqués par des
cercles sur le schema), on en déduit les valeurs
de
sur les points de grille pairs (indiqués par des
cercles sur le schema), on en déduit les valeurs
de
 (et donc de
(et donc de
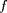 ) à l'instant
) à l'instant
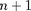 impair sur les points de grille impair (indiqués par des
triangles) avec
impair sur les points de grille impair (indiqués par des
triangles) avec
![n+1 n n n n u i = (1/2)[u i+1+u i- 1]- (Dt/2Dx)[f i+1 - f i- 1]](images-TeX4ht/mhd19x.gif)
 à l'instant
à l'instant
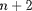 pair sur les points de grille pairs avec
pair sur les points de grille pairs avec
![n+2 n n+1 n+1 u i = u i- (Dt/Dx)[f i+1 - fi- 1 ]](images-TeX4ht/mhd22x.gif)
 qui nous interesse ne sera connue qu'aux instants
qui nous interesse ne sera connue qu'aux instants
 pairs sur les points grille
pairs sur les points grille
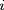 pairs, et que la grille des indices spatiaux et
temporelles impairs ne sert qu'à des calculs
intermédiaires.
pairs, et que la grille des indices spatiaux et
temporelles impairs ne sert qu'à des calculs
intermédiaires.