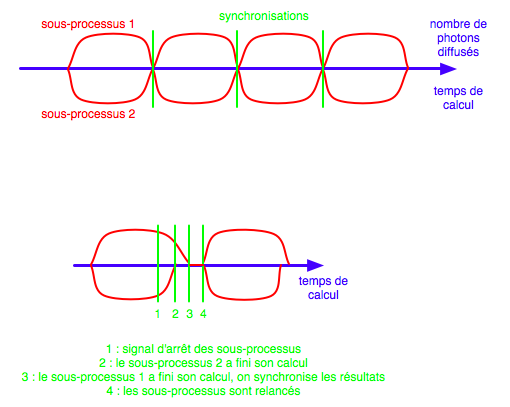
Nous allons décrire dans cette section l'algorithme qui nous a permis de réaliser cette statistique sur les trajectoires de sortie des photons.
On considère un faisceau de photons dirigé vers un nuage diffusif représenté dans notre cas par une couche à deux dimensions de largeur fixée par l'utilisateur. On exprime la largeur de la couche diffusive en unité de libre parcours moyen (λ), au lieu d'utiliser la densité de particules et la section efficace. Cette approche permet de simplifier le problème.
On considère un faisceau de photons dirigé vers un nuage diffusif représenté dans notre cas par une couche à deux dimensions de largeur fixée par l'utilisateur. On exprime la largeur de la couche diffusive en unité de libre parcours moyen (λ), au lieu d'utiliser la densité de particules et la section efficace. Cette approche permet de simplifier le problème.
Schéma explicatif
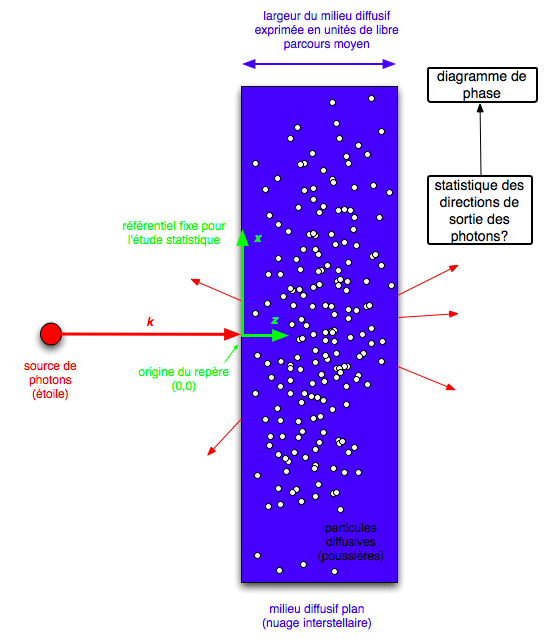

La trajectoire du photon est déterminée via deux paramètres : une distance et un couple d'angles qui sont tous tirés aléatoirements grâce à un générateur de nombre pseudo-aléatoires. La position est ainsi connue au fur et à mesure des diffusions successives. Lorsque le photon sort du nuage (sa position par rapport à l'axe z est au-delà de la largeur du nuage), on passe au photon suivant.
La distance parcourue par le photon est tirée aléatoirement suivant une loi de Poisson (loi exponentielle). Pour cela on s'intéresse à la fonction de répartition telle que : f(x)->F(u).
Si l'on considère F comme étant la fonction de répartition d'une variable aléatoire continue X, alors la variable aléatoire F(X) est uniforme entre 0 et 1. On sait que si deux fonctions de répartition sont identiques, alors les variables aléatoires associées sont égales. On peut donc écrire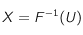 . On peut utiliser un changement de variable pour générer des nombres aléatoires X sous une loi F.
On part de la loi exponentielle avec
. On peut utiliser un changement de variable pour générer des nombres aléatoires X sous une loi F.
On part de la loi exponentielle avec 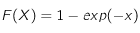 .
On peut en déduire :
.
On peut en déduire :
Si l'on considère F comme étant la fonction de répartition d'une variable aléatoire continue X, alors la variable aléatoire F(X) est uniforme entre 0 et 1. On sait que si deux fonctions de répartition sont identiques, alors les variables aléatoires associées sont égales. On peut donc écrire
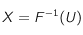 . On peut utiliser un changement de variable pour générer des nombres aléatoires X sous une loi F.
On part de la loi exponentielle avec
. On peut utiliser un changement de variable pour générer des nombres aléatoires X sous une loi F.
On part de la loi exponentielle avec 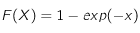 .
On peut en déduire :
.
On peut en déduire :
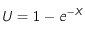
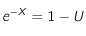
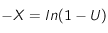
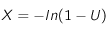
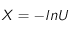
 U étant tiré au hasard par le générateur, X est donc un nombre aléatoire entre 0 et 1.
U étant tiré au hasard par le générateur, X est donc un nombre aléatoire entre 0 et 1.
- Si la distance tirée est supérieure à la largeur du nuage, le photon n'est pas diffusé (il traverse directement le nuage sans interaction) et on passe alors au photon suivant.
- Si la distance tirée est inférieure à la largeur du nuage (c'est à dire dans le nuage), le photon est diffusé. On tire alors un angle déterminant la direction post-diffusion du photon.
Remarque : Afin d'optimiser le temps de calcul, nous avons utilisé les probabilités conditionnelles afin qu'un photon lancé soit un photon diffusé. Cela permet de gagner un temps considérable au niveau du calcul. On exprime cette probabilité ainsi :
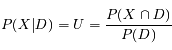
On en déduit une loi de tirage pour la première distance de pénétration dans le nuage :
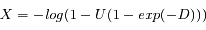
On s'assure ainsi que tous les photons soient diffusés lorsqu'ils entrent dans le nuage diffusif.
La distance étant tirée il faut à présent générer deux angles (θ, ) qui détermineront la direction du photon après sa diffusion.
) qui détermineront la direction du photon après sa diffusion.
Afin de suivre cette trajectoire, nous considérons deux référentiels distincts : le référentiel du point d'entrée dans le nuage (voir schéma 1) ainsi qu'un référentiel centré sur la particule diffusive.
Le référentiel d'entrée dans le nuage (R): il possède une base orthonormée directe (e1,e2,e3), avec e3 (axe z sur le schéma 1) perpendiculaire au plan formé par le nuage. C'est par rapport à ce repère que l'on positionne le photon dans le nuage.
Le référentiel de diffusion (R'): ce référentiel possède lui aussi une base orthonormée directe (e1',e2',e3') avec e3' dirigé suivant le vecteur d'onde du photon avant diffusion.
Si on considère les angles (θ, ) comme étant les coordonnées sphériques du vecteur d'onde unitaire dans R, on peut déterminer entièrement le référentiel R' suivant deux rotations successives.
) comme étant les coordonnées sphériques du vecteur d'onde unitaire dans R, on peut déterminer entièrement le référentiel R' suivant deux rotations successives.
La génération aléatoire de ces deux angles fait intervenir le type de la diffusion. Dans cet applet, nous traitons deux cas seulement (bien qu'il en existe d'autres): la diffusion isotrope et la diffusion Rayleigh. La diffusion isotrope, comme son nom l'indique, produit des angles sans directions privilégiées. La diffusion Rayleigh, quant à elle, a tendance à focaliser les angles de diffusion sur les directions "avant" et "arrière" du vecteur d'onde du photon avant diffusion. Les deux prochaines sections sont dédiées à la description des algorithmes permettant de générer ces angles dans chacun des types de diffusion abordés ici.
 ) qui détermineront la direction du photon après sa diffusion.
) qui détermineront la direction du photon après sa diffusion.
Afin de suivre cette trajectoire, nous considérons deux référentiels distincts : le référentiel du point d'entrée dans le nuage (voir schéma 1) ainsi qu'un référentiel centré sur la particule diffusive.
Le référentiel d'entrée dans le nuage (R): il possède une base orthonormée directe (e1,e2,e3), avec e3 (axe z sur le schéma 1) perpendiculaire au plan formé par le nuage. C'est par rapport à ce repère que l'on positionne le photon dans le nuage.
Le référentiel de diffusion (R'): ce référentiel possède lui aussi une base orthonormée directe (e1',e2',e3') avec e3' dirigé suivant le vecteur d'onde du photon avant diffusion.
Si on considère les angles (θ,
 ) comme étant les coordonnées sphériques du vecteur d'onde unitaire dans R, on peut déterminer entièrement le référentiel R' suivant deux rotations successives.
) comme étant les coordonnées sphériques du vecteur d'onde unitaire dans R, on peut déterminer entièrement le référentiel R' suivant deux rotations successives.
La génération aléatoire de ces deux angles fait intervenir le type de la diffusion. Dans cet applet, nous traitons deux cas seulement (bien qu'il en existe d'autres): la diffusion isotrope et la diffusion Rayleigh. La diffusion isotrope, comme son nom l'indique, produit des angles sans directions privilégiées. La diffusion Rayleigh, quant à elle, a tendance à focaliser les angles de diffusion sur les directions "avant" et "arrière" du vecteur d'onde du photon avant diffusion. Les deux prochaines sections sont dédiées à la description des algorithmes permettant de générer ces angles dans chacun des types de diffusion abordés ici.
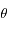 .
.
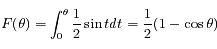
![[0,1]](eq_tex_diffusion_doc/equation28.png) , alors:
, alors:
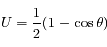
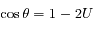
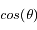 est donc uniforme entre -1 et 1. Par conséquent, nous utiliserons cette variable plutôt que
est donc uniforme entre -1 et 1. Par conséquent, nous utiliserons cette variable plutôt que 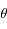 . Il y a par contre un désavantage à cause de la présence des pôles en
. Il y a par contre un désavantage à cause de la présence des pôles en 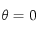 et
et 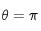 . Pour s'en affranchir, nous plongeons la sphère dans l'espace euclidien
. Pour s'en affranchir, nous plongeons la sphère dans l'espace euclidien 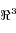 , et l'on rammène tous les points tirés aléatoirement sur la sphère unité.
, et l'on rammène tous les points tirés aléatoirement sur la sphère unité.
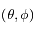 du vecteur d'onde sortant du nuage.
du vecteur d'onde sortant du nuage.
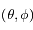 de sortie du nuage des photons. Pour tracer ce diagramme, on échantillonne
de sortie du nuage des photons. Pour tracer ce diagramme, on échantillonne 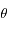 sur un certain nombre d'intervalles. De nos angles de sortie, on en déduit quel intervalle incrémenter.
sur un certain nombre d'intervalles. De nos angles de sortie, on en déduit quel intervalle incrémenter.
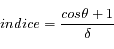

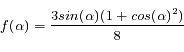
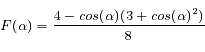
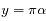 . On peut donc inverser la fonction de répartition (calculée à partir de la fonction de phase) en utilisant une méthode de Newton. On génère un nombre aléatoire u entre 0 et 1. On en déduit un angle
. On peut donc inverser la fonction de répartition (calculée à partir de la fonction de phase) en utilisant une méthode de Newton. On génère un nombre aléatoire u entre 0 et 1. On en déduit un angle 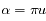 compris entre
compris entre ![[0,\pi]](eq_tex_diffusion_doc/equation36.png) . L'élément de correction
. L'élément de correction 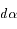 est de la forme:
est de la forme:
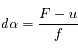
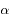 afin que la distribution statistique globale de ces angles suive bien une loi de diffusion de Rayleigh:
afin que la distribution statistique globale de ces angles suive bien une loi de diffusion de Rayleigh:
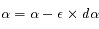
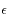 un critère de convergence fixé à 0.8 dans notre cas.
un critère de convergence fixé à 0.8 dans notre cas.
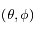 , on fait subir une rotation au couple
, on fait subir une rotation au couple 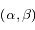 (avec
(avec 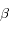 un angle généré aléatoirement entre
un angle généré aléatoirement entre ![[0,2\pi]](eq_tex_diffusion_doc/equation34.png) ) conformément à ce qui a été décrit plus haut.
Cette rotation nous permet de passer du référentiel du photon au référentiel d'entrée.
) conformément à ce qui a été décrit plus haut.
Cette rotation nous permet de passer du référentiel du photon au référentiel d'entrée.