Simulation: Un modèle numérique de la structure interne des étoiles
Auteur: Daniel Péquignot (documentation)
Auteur: Alain Hui-Bon-Hoa (version JAVA du programme)
Introduction:
Une étoile peut se définir comme un astre autogravitant, connexe, opaque
et intrinsèquement lumineux. La phase lumineuse d'une étoile
étant nécessairement de durée finie, l'objet compact qui lui survit
éventuellement est encore à ranger parmi les étoiles.
Une étoile transforme de l'énergie potentielle "macroscopique"
(contraction gravitationnelle) et "microscopique" (fusion de noyaux
atomiques) en énergie cinétique microscopique locale (pression), en
rayonnement (émission de photons et de neutrinos à la surface)
et en énergie mécanique (rotation, vents stellaires, explosions).
L'énergie disponible par particule ne sera significative que si la masse
autogravitante est suffisamment élevée : une étoile se distingue
fondamentalement d'une planète par sa masse.
Une fraction dominante de la matière baryonique détectable de
l'Univers semble se trouver sous forme d'étoiles. En rejetant dans le
milieu interstellaire une matière enrichie en éléments plus lourds
que l'hydrogène (pour de futures générations d'étoiles) et en
fixant une partie de la matière sous forme de restes compacts
inertes, les étoiles constituent le moteur principal de l'évolution
cosmique.
Que nous soyons pour l'essentiel formés de "poussières d'étoiles" est
maintenant bien établi. Que notre étoile, le Soleil, soit, au même titre que
la Terre, la condition première de notre existence est une évidence. Une
quête de nos origines passe par une connaissance de la nature des
étoiles.
Plus modestement, l'observation des étoiles a dû jouer un rôle dans la
structuration de l'esprit humain depuis les temps préhistoriques.
Aujourd'hui, la théorie de la structure et de l'évolution des étoiles, la plus
élaborée de l'Astrophysique, est une théorie vivante et créative, à la
croisée d'une physique sophistiquée et d'une réalité observationnelle
toujours plus diversifiée et contraignante.
Mais un attrait de cette théorie est que la mise en oeuvre de quelques
hypothèses et lois physiques fondamentales permet d'accéder directement
à une compréhension profonde et déjà raisonablement quantitative de ce
qu'est une étoile. La luminosité d'une étoile se ramène en ordre de
grandeur à une combinaison de constantes physiques fondamentales,
tandis que son rayon est d'abord une manifestation de l'effet tunnel.
Cependant, l'épuisement progressif du combustible nucléaire entraîne une
évolution étonnante, encore incomplètement élucidée, des paramètres
stellaires. Cette évolution, insoupçonable si l'on s'en tient à une approche
dimensionnelle, n'est révélée qu'à l'aide de modèles numériques résolvant
les équations qui régissent la structure des étoiles. C'est à la construction
d'un tel modèle, simplifié mais déjà réaliste, qu'est consacré ce
chapitre.
Le comportement des étoiles est rythmé par les échelles de temps
d'évolution dynamique, thermique et nucléaire, qui, pendant l'essentiel de
la vie d'une étoile, diffèrent les unes des autres par plusieurs ordres de
grandeur. Hormis quelques phases critiques et en ignorant les
conséquences d'éventuelles pulsations, sur des durées de l'ordre de
l'échelle de temps thermique, l'énergie gravitationnelle et les paramètres
thermodynamiques de l'étoile restent pratiquement inchangés, l'évolution
se résumant à la lente transmutation de quelques éléments dans les zones
de fusion thermonucléaire. Dans ces états quasi-stationnaires, la
description de la structure de l'étoile se trouve grandement simplifiée
parce que le paramètre temporel peut être sans grand dommage ignoré.
Le modèle d'étoile présenté ici est construit dans l'approximation
stationnaire.
L'appliquette est disponible en suivant ce lien.
Retour au menu des appliquettes.
Equations de la structure interne des étoiles.
La physique et l'évolution des étoiles sont considérés dans
l'excellent ouvrage de R. Kippenhahn et A. Weigert Stellar
Structure & Evolution (A&A library, Springer-Verlag), qui
font référence aux nombreuses monographies antérieures.
Représentons donc en première approximation une étoile
comme une structure gazeuse à symétrie sphérique en
équilibre hydrostatique et en état stationnaire de masse
M, de rayon R et de luminosité L.
La position à l'intérieur de cette sphère est commodément
représentée par la masse
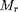 contenue dans la sphère de rayon
contenue dans la sphère de rayon
 (
(
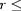 R) :
R) :
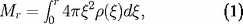
où
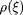 est la masse volumique au rayon
est la masse volumique au rayon
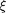 . Rayon et masse sont reliés par l'équation différentielle :
. Rayon et masse sont reliés par l'équation différentielle :
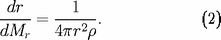
L'équation de l'équilibre hydrostatique :

où
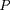 est la pression totale et
est la pression totale et
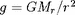 l'intensité du champ de gravité (
l'intensité du champ de gravité (
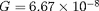 constante de la gravitation), se réécrit :
constante de la gravitation), se réécrit :
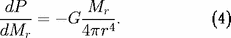
En pratique, dans le logiciel présenté ici, la masse volumique
 sera préférée à
sera préférée à
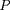 comme fonction à intégrer. L'équation (4) est substituée en
appliquant :
comme fonction à intégrer. L'équation (4) est substituée en
appliquant :
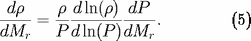
Si
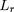 est la puissance thermique nette sortant de la sphère
est la puissance thermique nette sortant de la sphère
 et
et
 l'énergie thermique produite par unité de masse et par seconde
au niveau
l'énergie thermique produite par unité de masse et par seconde
au niveau
 du fait de la fusion nucléaire, la conservation de l'énergie en
état stationnaire se traduit par :
du fait de la fusion nucléaire, la conservation de l'énergie en
état stationnaire se traduit par :

Introduisons la notation (avec
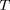 la température) :
la température) :
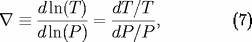
de sorte que :
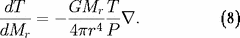
L'opacité
 par unité de masse de gaz est définie par la relation :
par unité de masse de gaz est définie par la relation :
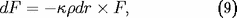
où
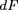 est l'extinction subie par un flux de rayonnement
est l'extinction subie par un flux de rayonnement
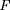 sur la distance
sur la distance
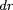 . La quantité
. La quantité
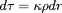 est l'élément d'épaisseur optique et 1/
est l'élément d'épaisseur optique et 1/
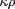 le libre parcours moyen des photons.
le libre parcours moyen des photons.
La matière stellaire étant très opaque, le champ de rayonnement
y est presque isotrope et presqu'exactement celui d'un corps
noir à la température locale
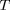 , d'où la densité de rayonnement :
, d'où la densité de rayonnement :

avec
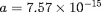 constante de la radiation. A l'approximation de l'équation de
diffusion, le flux net de rayonnement est (
constante de la radiation. A l'approximation de l'équation de
diffusion, le flux net de rayonnement est (
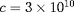 cm/s vitesse de la lumière) :
cm/s vitesse de la lumière) :
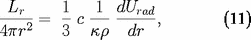
qui peut se récrire, compte tenu de (8) :
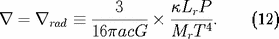
Mais, lorsque
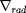 devient plus grand que la valeur adiabatique
devient plus grand que la valeur adiabatique
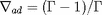 , avec
, avec
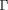 l'exposant adiabatique (
l'exposant adiabatique (
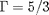 pour un gaz parfait monoatomique), le gaz entre spontanément
en mouvement de convection, transportant alors efficacement
une énergie thermique supplémentaire et ramenant en première
approximation le gradient de température à sa valeur
adiabatique :
pour un gaz parfait monoatomique), le gaz entre spontanément
en mouvement de convection, transportant alors efficacement
une énergie thermique supplémentaire et ramenant en première
approximation le gradient de température à sa valeur
adiabatique :
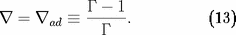
On a donc finalement :
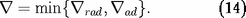
L'intégration des quatre équations différentielles du premier
ordre couplées (2), (4)+(5), (6) et (8)+(14) pour une étoile
statique stationnaire nécessite la donnée de quatre conditions
aux limites.
Conditions aux limites.
Adoptant
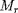 comme variable principale, il existe deux conditions au
centre :
comme variable principale, il existe deux conditions au
centre :
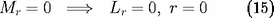
et deux à la "surface" de l'étoile, assimilée ici à la photosphère
de rayon R, d'où échappe directement l'essentiel des
photons :
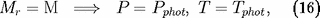
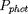 et
et
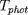 résultant en principe d'un modèle décrivant l'atmosphère de
l'étoile. Un modèle détaillé d'atmosphère, absent du présent
modèle de structure interne, peut devenir nécessaire pour
résoudre l'équation de transfert du rayonnement et
traiter explicitement les différents mode de transport de
l'énergie.
résultant en principe d'un modèle décrivant l'atmosphère de
l'étoile. Un modèle détaillé d'atmosphère, absent du présent
modèle de structure interne, peut devenir nécessaire pour
résoudre l'équation de transfert du rayonnement et
traiter explicitement les différents mode de transport de
l'énergie.
Notons que R =
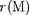 et L =
et L =
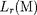 résulteront de la résolution des équations de structure
interne.
résulteront de la résolution des équations de structure
interne.
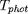 est identifiée à la température effective
est identifiée à la température effective
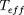 de l'étoile, c'est-à-dire à la température du corps noir de même
puissance par unité de surface :
de l'étoile, c'est-à-dire à la température du corps noir de même
puissance par unité de surface :
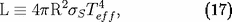
(
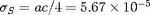 constante de Stefan).
constante de Stefan).
Une description simple du transfert du rayonnement
(approximation semi-isotrope d'Eddington) montre que la
profondeur optique de la photosphère est
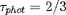 et donc que, en ordre de grandeur, compte tenu de (3) et
(9) :
et donc que, en ordre de grandeur, compte tenu de (3) et
(9) :
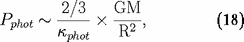
où
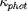 est l'opacité photosphérique. Cette expression fournit une
masse volumique
est l'opacité photosphérique. Cette expression fournit une
masse volumique
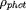 .
.
Pour obtenir un modèle, il faut encore spécifier les lois
décrivant les deux fonctions physiques rencontrées et
l'équation d'état reliant les grandeurs thermodynamiques :
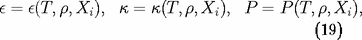
dans lesquelles
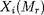 symbolise la composition chimique et isotopique.
symbolise la composition chimique et isotopique.
Processus physiques et équation d'état.
Composition chimique.
Il est d'usage de noter
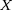 la masse d'hydrogène par unité de masse de matière
stellaire,
la masse d'hydrogène par unité de masse de matière
stellaire,
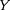 celle d'hélium et
celle d'hélium et
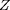 la somme de celles des autres éléments (surtout
C, N et O). Les valeurs rencontrées dans la photosphère
solaire (
la somme de celles des autres éléments (surtout
C, N et O). Les valeurs rencontrées dans la photosphère
solaire (
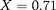 ,
,
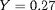 ,
,
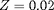 ) sont typiques de celles qu'aura une étoile de
composition encore homogène peu de temps après
sa formation (
) sont typiques de celles qu'aura une étoile de
composition encore homogène peu de temps après
sa formation (
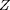 dépend cependant de la "population" d'étoiles
considérée).
dépend cependant de la "population" d'étoiles
considérée).
Cette description simplifiée de la composition
chimique est suffisante pour définir des formes
approchées des fonctions physiques.
En admettant que l'oxygène représente bien la
moyenne des éléments lourds, on définit le poids
moléculaire moyen des ions, considérés seuls :
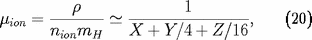
le poids moléculaire moyen par électron libre, lorsque le
gaz est complètement ionisé :
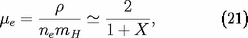
et le poids moléculaire moyen par particule libre, à
nouveau pour un gaz ionisé :
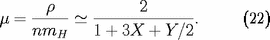
Dans ces expressions,
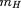 est la masse de l'atome d'hydrogène,
est la masse de l'atome d'hydrogène,
 la densités numérique totale de toutes les particules
libres,
la densités numérique totale de toutes les particules
libres,
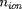 celle des ions et
celle des ions et
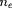 celle des électrons libres. Ces expressions de
celle des électrons libres. Ces expressions de
 et surtout de
et surtout de
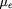 sont à modifier dans l'atmosphère des étoiles froides,
incomplètement ionisées.
sont à modifier dans l'atmosphère des étoiles froides,
incomplètement ionisées.
Equation d'état de la matière stellaire.
La pression est la somme de la pression de radiation
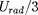 , donnée par (10), et de la pression gazeuse :
, donnée par (10), et de la pression gazeuse :
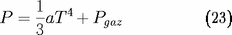
Pour un gaz parfait ordinaire :
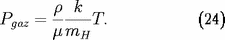
Si le gaz de noyaux reste parfait en presque toutes
circonstances (sauf dans les étoiles à neutrons),
le gaz d'électrons, plus sensible au principe
d'exclusion de Pauli, peut devenir dégénéré dans des
conditions stellaires. Il est alors plus commode de
distinguer la pression des ions de la pression
électronique :
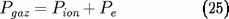
avec :
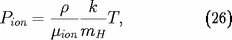
et, pour la composante non dégénérée de la pression
électronique :
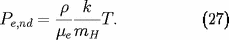
La pression du gaz de Fermi d'électrons prend une
forme simple dans les cas limites d'un gaz
complètement dégénéré soit non relativiste, soit ultra
relativiste :
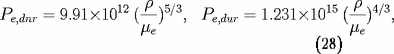
la transition semi-relativiste se produisant
pour
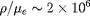 g/cm
g/cm
 . Une forme approchée de la pression de dégénérescence
est alors :
. Une forme approchée de la pression de dégénérescence
est alors :
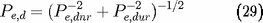
et la pression totale du gaz d'électrons est
approximativement :
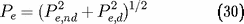
Opacité du gaz.
Pour un champ de rayonnement proche de celui
du corps noir, l'opacité moyenne
 est une moyenne harmonique de l'opacité monochromatique
est une moyenne harmonique de l'opacité monochromatique
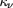 , pondérée par la dérivée de la fonction de Planck
, pondérée par la dérivée de la fonction de Planck
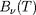 ("moyenne de Rosseland") :
("moyenne de Rosseland") :
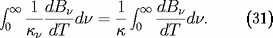
Cette expression peut devenir imprécise aux
profondeurs optiques faibles.
La diffusion électronique est indépendante de la
fréquence et donne lieu à une opacité :
![ke = 0.20(1+X )[1+2.7 × 1011r/T 2]- 1[1+(T /4.5 × 108)0.86] - 1, (32)](images-TeX4ht/stellar90x.gif)
où les deux termes entre crochets apportent des
corrections tenant compte de la dégénérescence et de la
relativite restreinte (
 et/ou
et/ou
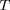 très élevées).
très élevées).
L'absorption des photons par les atomes et
les ions (photoexcitation, photoionisation,
absorption libre-libre) est donnée en toute
première approximation par la loi d'opacité de
Kramers :
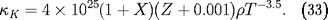
Dans les gaz froids relativement neutres, l'ion
faiblement lié H
 , formé par recombinaison d'électrons libres issus de
métaux partiellement ionisés avec l'atome d'hydrogène,
ainsi que les molécules deviennent des absorbants
importants. En ordre de grandeur, on adopte
pour l'opacité du milieu dans le régime basse
température (d'autres sources d'opacité que
H
, formé par recombinaison d'électrons libres issus de
métaux partiellement ionisés avec l'atome d'hydrogène,
ainsi que les molécules deviennent des absorbants
importants. En ordre de grandeur, on adopte
pour l'opacité du milieu dans le régime basse
température (d'autres sources d'opacité que
H
 sont implicitement ajoutées vers 10
sont implicitement ajoutées vers 10
 K) :
K) :
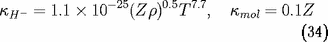
(
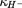 est utilisé harmoniquement).
est utilisé harmoniquement).
La conduction électronique, importante lorsque le gaz
devient dense et dégénéré, donne lieu à un transport
d'énergie thermique fonctionnellement analogue à celui
du transport radiatif (flux net proportionnel au
gradient de
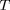 ) et peut donc être formellement représentée au moyen
d'une "opacité conductive", dont une expression
approchée est :
) et peut donc être formellement représentée au moyen
d'une "opacité conductive", dont une expression
approchée est :
![- 7 2 6 2/3 kcond = 2.6 × 10 (X +2Y +8Z )(T /r) [1+(r/2 × 10 ) ]. (35)](images-TeX4ht/stellar100x.gif)
Le calcul de l'opacité moyenne proprement
dite
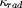 est alors effectué à l'aide de :
est alors effectué à l'aide de :
![1 1 k = k + [------ + -------------]- 1. (36) rad mol k - (k + k ) H e K](images-TeX4ht/stellar102x.gif)
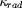 présente un maximum prononcé pour
présente un maximum prononcé pour
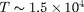 K (ionisation de l'hydrogène).
K (ionisation de l'hydrogène).
L'opacité moyenne à utiliser effectivement dans
l'expression (12) pour
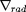 est :
est :
![1 1 k = [------+ -------]- 1. (37) krad kcond](images-TeX4ht/stellar106x.gif)
Convection.
Le calcul de
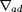 (équation 13) s'effectue directement à partir des
grandeurs thermodynamiques car
(équation 13) s'effectue directement à partir des
grandeurs thermodynamiques car
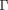 n'est pas connu a priori :
n'est pas connu a priori :
![@ ln(P ) @ ln(r) @ ln(P ) - 1 \~/ ad = [ ----------|s ----------|s + ----------|r ] . @ ln(r) @ ln(T ) @ ln(T ) (38)](images-TeX4ht/stellar109x.gif)
Le transport convectif, qui garantit un gradient
de température quasi adiabatique à un haut
degré d'approximation à l'intérieur des étoiles,
devient inefficace dans leurs couches extérieures
très peu denses. Ce gradient devient donc
intermédiaire entre le gradient adiabatique et le
gradient radiatif. Le flux convectif d'énergie
thermique
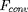 doit alors être calculé en détail en fonction des
caractéristiques du milieu et ajouté au flux
radiatif
doit alors être calculé en détail en fonction des
caractéristiques du milieu et ajouté au flux
radiatif
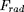 . La conservation du flux net impose :
. La conservation du flux net impose :
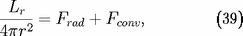
où
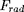 est encore obtenu à l'aide de l'expression (12)
est encore obtenu à l'aide de l'expression (12)
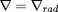 , mais dans laquelle
, mais dans laquelle
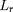 a été remplacée par
a été remplacée par
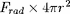 . Rappelons cependant que, dans les couches les plus
externes, les expression (12) et (31) elles-mêmes cessent
d'être précises.
. Rappelons cependant que, dans les couches les plus
externes, les expression (12) et (31) elles-mêmes cessent
d'être précises.
Le détail de la convection, habituellement traité grâce à
une théorie phénoménologique approchée, dite "de la
longueur de mélange", n'est pas considéré dans le
présent modèle.
Taux de production d'énergie nucléaire.
Aux très basses énergies associées aux températures
stellaires, la fusion des noyaux atomiques est rendue
possible grâce à l'effet tunnel. Pour une collision
d'énergie
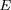 entre particules de charges
entre particules de charges
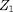 et
et
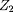 et de masse réduite
et de masse réduite
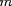 , la probabilité de traverser la barrière coulombienne
répulsive est
, la probabilité de traverser la barrière coulombienne
répulsive est
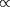 exp(
exp(
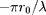 ), avec
), avec
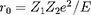 la distance d'approche classique et
la distance d'approche classique et
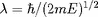 la longueur d'onde De Broglie. Pour une distribution
de Maxwell des noyaux, la probabilité de rencontrer
une paire d'énergie
la longueur d'onde De Broglie. Pour une distribution
de Maxwell des noyaux, la probabilité de rencontrer
une paire d'énergie
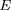 est
est
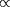 exp(
exp(
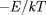 ). L'intégrale du produit de ces deux probabilités,
principal facteur dépendant de
). L'intégrale du produit de ces deux probabilités,
principal facteur dépendant de
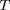 dans le taux de fusion, est
dans le taux de fusion, est
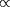 exp(
exp(
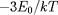 ), où
), où
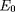 correspond au maximum de ce produit ("pic de
Gamow"). Le nombre de fusions /g/s est donné
par :
correspond au maximum de ce produit ("pic de
Gamow"). Le nombre de fusions /g/s est donné
par :
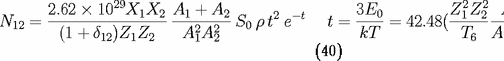
avec
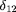 le symbole de Kronecker,
le symbole de Kronecker,
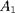 et
et
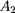 les poids atomiques,
les poids atomiques,
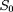 (en "kev-barn") la partie proprement nucléaire de la
section efficace et
(en "kev-barn") la partie proprement nucléaire de la
section efficace et
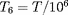 K. L'expression (40) est modifiée lorsque la section
nucléaire présente une résonance d'énergie voisine de
celle du pic de Gamow.
K. L'expression (40) est modifiée lorsque la section
nucléaire présente une résonance d'énergie voisine de
celle du pic de Gamow.
La fusion de protons
 H en noyaux
H en noyaux
 He s'effectue soit par des chaînes de réactions initiées
par la fusion proton-proton
He s'effectue soit par des chaînes de réactions initiées
par la fusion proton-proton
 H +
H +
 H
H
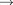
 H et impliquant seulement la fusion de protons avec
des sous-produits de cette fusion initiale ("chaînes
pp"), soit par des réactions dans lesquelles une
série d'isotopes de C, N et O jouent le rôle de
catalyseurs, globalement conservés au cours
de cycles successifs ("cycle CNO"). L'énergie
dégagée est d'environ 6.5 MeV par nucléon.
Les taux respectifs de production d'énergie
par unité de masse (en erg/s/g) sont donnés
par :
H et impliquant seulement la fusion de protons avec
des sous-produits de cette fusion initiale ("chaînes
pp"), soit par des réactions dans lesquelles une
série d'isotopes de C, N et O jouent le rôle de
catalyseurs, globalement conservés au cours
de cycles successifs ("cycle CNO"). L'énergie
dégagée est d'environ 6.5 MeV par nucléon.
Les taux respectifs de production d'énergie
par unité de masse (en erg/s/g) sont donnés
par :
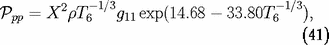
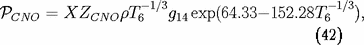
où :
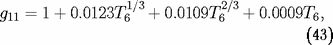
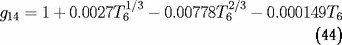
sont des facteurs tenant compte de la variation des
section nucléaires avec
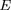 . La fraction de masse sous forme de CNO,
. La fraction de masse sous forme de CNO,
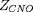 , vaut 2
, vaut 2
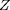 /3 dans le programme.
/3 dans le programme.
L'effet d'écran dû aux électrons libres environnant les
noyaux atomiques revient à remplacer l'énergie
cinétique incidente
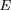 par
par
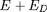 , avec
, avec
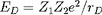 l'énergie de Debye (
l'énergie de Debye (
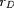 rayon de Debye), et donc à multiplier le taux de fusion
par le facteur d'écran :
rayon de Debye), et donc à multiplier le taux de fusion
par le facteur d'écran :
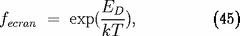
avec, dans les limites de l'écran "faible" :
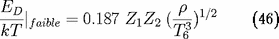
et de l'écran "fort" (
 élevée,
élevée,
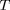 faible) :
faible) :
![ED 5/3 5/3 (r/me)1/3 -----|fort = 0.205 [(Z1+Z2)5/3 - Z 1 - Z 2 ]-------------. kT T6 (47)](images-TeX4ht/stellar159x.gif)
Le taux de production d'énergie par fusion de
l'hydrogène est :
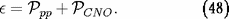
Le taux correspondant de décroissance de l'hydrogène
en g/s/g de matière stellaire, qui peut être introduit
dans une description quasi-statique de l'évolution, est
donné par :
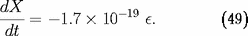
Les termes pp et CNO dominent aux basses et hautes
températures respectivement.
Une fois l'hydrogène totalement épuisé, l'élément
susceptible de fusionner est l'hélium, mais, dans les
conditions stellaires, le premier isotope stable au-delà
de
 He est
He est
 C, produisant environ 0.6 MeV par nucléon et exigeant
la fusion de trois particules
C, produisant environ 0.6 MeV par nucléon et exigeant
la fusion de trois particules
 , rendue possible par l'existence d'un noyau
métastable
, rendue possible par l'existence d'un noyau
métastable
 Be et d'une résonance
Be et d'une résonance
 C. Le taux de production d'énergie par fusion
3
C. Le taux de production d'énergie par fusion
3
 est, en fonction de
est, en fonction de
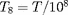 K :
K :
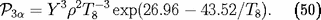
Le taux correspondant de croissance des éléments plus
lourds que l'hélium (
 C et
C et
 O) serait, à nouveau en g/s/g :
O) serait, à nouveau en g/s/g :
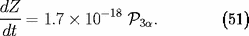
Les réactions de fusion de noyaux plus lourds n'ont pas
été introduites.
Neutrinos.
Chaque fusion de deux protons s'accompagne
de l'émission d'un neutrino. Le nombre de
neutrinos produit par seconde par ce processus
est calculé par le programme, mais non le
spectre en énergie. D'autres neutrinos, exigeant
l'introduction du réseau complet de réactions, ne
sont pas considérés ici.
Résolution des équations par la méthode du tir.
Principe.
Les quatre équations différentielles couplées à intégrer
pour
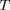 ,
,
 ,
,
 et
et
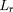 ayant une propension excessive à diverger aux
limites, il est interessant d'effectuer l'intégration
à la fois à partir de
ayant une propension excessive à diverger aux
limites, il est interessant d'effectuer l'intégration
à la fois à partir de
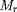 = 0 (vers l'extérieur) et de
= 0 (vers l'extérieur) et de
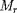 = M (vers l'intérieur) et de chercher par itération
à rendre les solutions continues en un point de
raccordement
= M (vers l'intérieur) et de chercher par itération
à rendre les solutions continues en un point de
raccordement
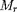 =
=
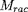 .
Les quatre paramètres de contour adoptés en pratique
sont, au centre, la température
.
Les quatre paramètres de contour adoptés en pratique
sont, au centre, la température
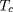 et la masse volumique
et la masse volumique
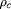 , à la surface, la température effective
, à la surface, la température effective
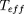 et la luminosité L (
et la luminosité L (
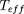 équivalente à R, moyennant (17)). L'intégration
peut être répétée en variant ces paramètres de tir,
ce qui permet d'évaluer la variation de l'écart sur
équivalente à R, moyennant (17)). L'intégration
peut être répétée en variant ces paramètres de tir,
ce qui permet d'évaluer la variation de l'écart sur
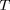 ,
,
 ,
,
 et
et
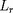 en
en
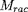 et d'améliorer ainsi le choix des paramètres de
contour pour l'itération suivante.
et d'améliorer ainsi le choix des paramètres de
contour pour l'itération suivante.
Exemples d'utilisation du programme.
Pour calculer un modèle, il faut entrer des paramètres stellaires
initiaux dans les différents champs de saisie et de lancer le calcul en cliquant sur le bouton.
Pour 1 masse solaire, vous constaterez que le résultat diffère du Soleil actuel, dont la
composition (
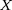 ,
,
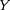 ) n'est plus homogène après
) n'est plus homogène après
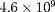 années d'évolution. Commentaire ? Commentez aussi la
variation des différentes variables avec la position : zone
de production d'énergie nucléaire, etc.
années d'évolution. Commentaire ? Commentez aussi la
variation des différentes variables avec la position : zone
de production d'énergie nucléaire, etc.
L'effet du choix des conditions aux limites peut être évalué
en inhibant le mode de convergence automatique et en
entrant soi-même des valeurs après chaque calcul (mode "apprentissage").
Recherchez les conditions dans lesquelles l'équation d'état
n'est plus celle d'un gaz parfait. La dégénérescence est-elle
significative dans le Soleil ? Dans une étoile de masse plus
faible ?
En calculant des modèles pour une série de masses M de
composition chimique donnée, trouvez la relation masse-luminosité
L(M) théorique. Il est conseillé de modifier M progressivement
pour partir de conditions initiales raisonables facilitant la
convergence.
Que se passe-t-il pour des masses très supérieures à 100
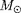 ou très inférieures à 0.5
ou très inférieures à 0.5
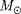 ? Explications ?
? Explications ?
Dans un diagramme HR (Hertzsprung-Russel) théorique,
chaque étoile est représentée par un point dans des axes
log(L) (L croissante vers le haut) versus log(
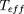 ) (
) (
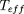 croissante vers la gauche). Reportez-y les résultats de
modèles d'étoiles déjà obtenus. Pour une composition solaire
uniforme, vous avez une représentation de la série principale
d'âge zéro (en anglais ZAMS pour "Zero Age Main Sequence").
croissante vers la gauche). Reportez-y les résultats de
modèles d'étoiles déjà obtenus. Pour une composition solaire
uniforme, vous avez une représentation de la série principale
d'âge zéro (en anglais ZAMS pour "Zero Age Main Sequence").
Découvrez, pour différentes valeurs de M, où se situent les
zones convectives à l'intérieur des étoiles. Explications ?
Cette liste d'applications n'est évidemment pas
exhaustive !
Suggestions de modifications et d'améliorations.
Le contenu physique de ce modèle peut être amélioré
ou enrichi de multiples façons, plus ou moins difficiles à
mettre en oeuvre.
L'opacité
peut par exemple être obtenue par interpolation dans une
table réaliste (malheureusement assez encombrante). Une
procédure d'interpolation remplacerait alors la procédure
de calcul Opacity.
D'autres extensions peuvent concerner le réseau de réactions
nucléaires. En introduisant suffisamment d'isotopes intervenant
dans les chaînes pp (
 Be,
Be,
 B, etc.), il devient par exemple possible de calculer un
spectre de neutrinos plus complet et de comparer les résultats
à ceux donnés dans les innombrables publications dédiées
au "mystère des neutrinos solaires".
B, etc.), il devient par exemple possible de calculer un
spectre de neutrinos plus complet et de comparer les résultats
à ceux donnés dans les innombrables publications dédiées
au "mystère des neutrinos solaires".
Au cours du temps, le coeur des étoiles s'enrichit en hélium
au détriment de l'hydrogène et les étoiles deviennent chimiquement
inhomogènes dans la mesure où elles ne sont pas entièrement
convectives. On peut essayer de se faire une idée de la
structure d'étoiles évoluées ayant quitté la ZAMS (et les
placer dans le diagramme HR) en considérant un modèle
comportant deux zones de compositions différentes. Il pourrait
être commode de changer de composition au point de
raccordement
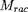 , la procédure Inward utilisant une composition modifiée
et la procédure Outward la composition habituelle. Le
sous-menu Composition pourrait être modifié pour afficher
cette nouvelle option. La valeur choisie pour
, la procédure Inward utilisant une composition modifiée
et la procédure Outward la composition habituelle. Le
sous-menu Composition pourrait être modifié pour afficher
cette nouvelle option. La valeur choisie pour
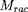 pourrait être motivée par des considérations sur la taille
de la zone convective centrale éventuelle des étoiles de la
ZAMS (voir plus haut).
pourrait être motivée par des considérations sur la taille
de la zone convective centrale éventuelle des étoiles de la
ZAMS (voir plus haut).
Lorsqu'une étoile a épuisé l'hydrogène dans ses régions
centrales, la fusion se poursuit à la frontière d'un
coeur d'hélium inerte à peu près isotherme, dans une
couche devenant de plus en plus fine et dans laquelle
certains gradients peuvent devenir très grands. Essayez
d'imaginer quelles approximations et quelles modifications
du programme pourraient être envisagées pour traiter ce
genre de situations et peut-être arriver à représenter une
géante rouge, dont l'enveloppe est entièrement convective.
Vous pouvez également activer la fusion 3
 en faisant appeler NuclearPowerAlpha par NuclearPower,
ce qui vous permet au moins d'étudier la ZAMS des étoiles
d'hélium pur. Plus ambitieux, vous pourriez vous intéresser
à des étoiles présentant un coeur d'hélium nucléairement
actif, entouré d'une enveloppe encore riche en hydrogène.
Notez que ces étoiles à coeur d'hélium continuent le plus
souvent à fusionner de l'hydrogène dans une couche fine
constituant la frontière du coeur, bien que l'une ou l'autre
source d'énergie puisse dominer selon les moments. Des
complications pourraient s'ensuivre...
en faisant appeler NuclearPowerAlpha par NuclearPower,
ce qui vous permet au moins d'étudier la ZAMS des étoiles
d'hélium pur. Plus ambitieux, vous pourriez vous intéresser
à des étoiles présentant un coeur d'hélium nucléairement
actif, entouré d'une enveloppe encore riche en hydrogène.
Notez que ces étoiles à coeur d'hélium continuent le plus
souvent à fusionner de l'hydrogène dans une couche fine
constituant la frontière du coeur, bien que l'une ou l'autre
source d'énergie puisse dominer selon les moments. Des
complications pourraient s'ensuivre...
Le programme nécessiterait des modifications pour
accepter des situations où la production d'énergie
thermonucléaire serait négligeable et l'étoile maintenue en
équilibre hydrostatique grâce à la pression du gaz dégénéré
d'électrons (naine blanche). D'autres aménagements
seraient nécessaires pour calculer la luminosité d'une telle
étoile, supposée maintenant à une température faible mais
non nulle (écart à l'état stationnaire strict).
Une modification de grande envergure du présent modèle
pourrait concerner la description des couches superficielles
de l'étoile : introduction d'un modèle d'atmosphère avec
convection traitée par la théorie de la longueur de mélange.
Une description réaliste des zones superficielles est en
effet nécessaire lorsqu'une zone convective profonde se
développe à partir de la surface (étoiles de température
effective faible).
Finalement, un code de modélisation, c'est aussi l'imagination
au pouvoir ! A condition de reprendre le détail des procédures
et des valeurs numériques, vous pouvez explorer à peu
de frais des mondes virtuels dans lesquels les fonctions
physiques, voire les constantes physiques fondamentales,
diffèrent de ce que nous connaissons. Essayez par exemple
de diviser ou de multiplier par 100 le taux de production
d'énergie nucléaire. Par 10
 ! Les résultats sont-ils très surprenants ? Commentez,
notamment selon la valeur de M. Vous pouvez de même
modifier ou supprimer tel ou tel terme de la loi d'opacité,
ou encore tester l'influence de la valeur de la constante de
la gravitation
! Les résultats sont-ils très surprenants ? Commentez,
notamment selon la valeur de M. Vous pouvez de même
modifier ou supprimer tel ou tel terme de la loi d'opacité,
ou encore tester l'influence de la valeur de la constante de
la gravitation
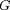 . L'altération des constantes physiques fondamentales, pour
être introduite de manière cohérente, peut vous amener à
remonter à l'expression littérale de coefficients numériques
contenant implicitement ces constantes.
. L'altération des constantes physiques fondamentales, pour
être introduite de manière cohérente, peut vous amener à
remonter à l'expression littérale de coefficients numériques
contenant implicitement ces constantes.
Liste des paramètres de l'appliquette:
-
label: masse
type: nombre
titre: Masse de l'étoile
unités: masse solaire
mode d'acquisition: champ
Masse du modèle de départ
-
label: tEff
type: nombre
titre: Température effective
unités: K
mode d'acquisition: champ
Estimation initiale de la température effective
-
label: luminosite
type: nombre
titre: Luminosité
unités: luminosité solaire
mode d'acquisition: champ
Estimation initiale de la luminosité
-
label: tCentre
type: nombre
titre: Température centrale
unités: K
mode d'acquisition: champ
Estimation initiale de la température centrale
-
label: dCentre
type: nombre
titre: Densité centrale
unités: cgs
mode d'acquisition: champ
Estimation initiale de la densité centrale
-
label: masseJ
type: nombre
titre: Fract. de masse au pt de jonction
unités:
mode d'acquisition: champ
Fraction de masse au point de jonction (entre 0 et 1)
-
label: apprendre
type: string
titre: Mode apprentissage
unités:
mode d'acquisition: case
A cocher pour lancer une seule itération. La correction des conditions aux limites s'effectue manuellement
-
label: jonction
type: string
titre: Point de jonction auto.
unités:
mode d'acquisition: case
A cocher pour une détermination automatique du point de jonction optimal
Mode d'emploi de l'appliquette:
Au lancement de l'appliquette, une fenêtre apparaît comme ci-dessous.
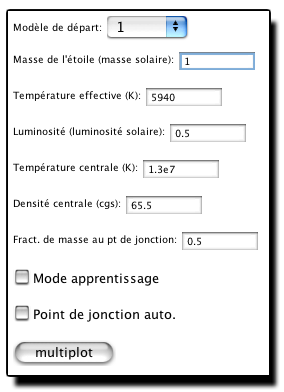
Une fois le calcul demandé, la fenêtre prend l'aspect illustré ci-dessous.
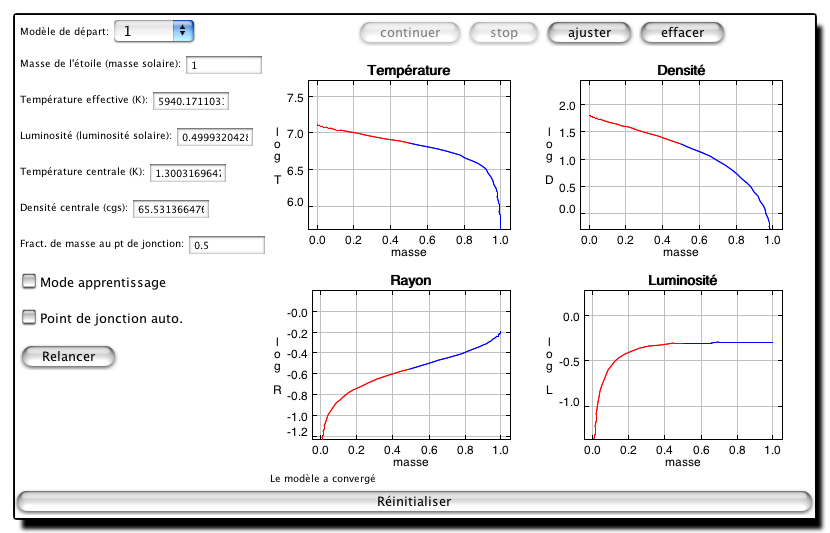
Le bouton "stop" permet de suspendre le calcul. Quand on clique dessus le tracé s'arrête, le bouton "stop" devient grisé et le bouton "continuer" peut être activé afin de poursuivre l'expérience.
Le bouton "ajuster" permet d'ajuster les échelles des diagrammes en fonction de leur contenu et "effacer" d'effacer les tracés.
Une action sur le bouton "Relancer" provoque le lancement d'un nouveau calcul, avec les nouvelles valeurs des paramètres s'il y a lieu.
Tout en bas, le bouton "Réinitialiser" ramène au premier écran.
L'appliquette est disponible en suivant ce lien.
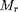 contenue dans la sphère de rayon
contenue dans la sphère de rayon
 (
(
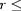 R) :
R) :
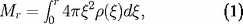
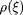 est la masse volumique au rayon
est la masse volumique au rayon
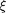 . Rayon et masse sont reliés par l'équation différentielle :
. Rayon et masse sont reliés par l'équation différentielle :
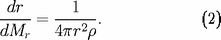

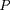 est la pression totale et
est la pression totale et
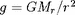 l'intensité du champ de gravité (
l'intensité du champ de gravité (
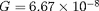 constante de la gravitation), se réécrit :
constante de la gravitation), se réécrit :
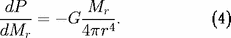
 sera préférée à
sera préférée à
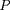 comme fonction à intégrer. L'équation (4) est substituée en
appliquant :
comme fonction à intégrer. L'équation (4) est substituée en
appliquant :
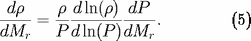
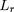 est la puissance thermique nette sortant de la sphère
est la puissance thermique nette sortant de la sphère
 et
et
 l'énergie thermique produite par unité de masse et par seconde
au niveau
l'énergie thermique produite par unité de masse et par seconde
au niveau
 du fait de la fusion nucléaire, la conservation de l'énergie en
état stationnaire se traduit par :
du fait de la fusion nucléaire, la conservation de l'énergie en
état stationnaire se traduit par :

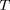 la température) :
la température) :
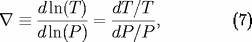
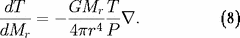
 par unité de masse de gaz est définie par la relation :
par unité de masse de gaz est définie par la relation :
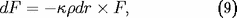
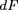 est l'extinction subie par un flux de rayonnement
est l'extinction subie par un flux de rayonnement
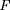 sur la distance
sur la distance
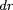 . La quantité
. La quantité
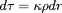 est l'élément d'épaisseur optique et 1/
est l'élément d'épaisseur optique et 1/
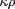 le libre parcours moyen des photons.
le libre parcours moyen des photons.
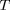 , d'où la densité de rayonnement :
, d'où la densité de rayonnement :

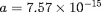 constante de la radiation. A l'approximation de l'équation de
diffusion, le flux net de rayonnement est (
constante de la radiation. A l'approximation de l'équation de
diffusion, le flux net de rayonnement est (
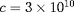 cm/s vitesse de la lumière) :
cm/s vitesse de la lumière) :
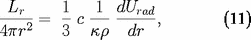
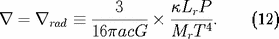
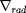 devient plus grand que la valeur adiabatique
devient plus grand que la valeur adiabatique
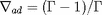 , avec
, avec
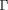 l'exposant adiabatique (
l'exposant adiabatique (
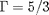 pour un gaz parfait monoatomique), le gaz entre spontanément
en mouvement de convection, transportant alors efficacement
une énergie thermique supplémentaire et ramenant en première
approximation le gradient de température à sa valeur
adiabatique :
pour un gaz parfait monoatomique), le gaz entre spontanément
en mouvement de convection, transportant alors efficacement
une énergie thermique supplémentaire et ramenant en première
approximation le gradient de température à sa valeur
adiabatique :
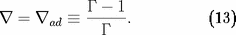
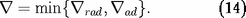
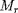 comme variable principale, il existe deux conditions au
centre :
comme variable principale, il existe deux conditions au
centre :
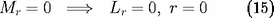
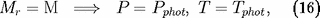
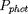 et
et
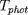 résultant en principe d'un modèle décrivant l'atmosphère de
l'étoile. Un modèle détaillé d'atmosphère, absent du présent
modèle de structure interne, peut devenir nécessaire pour
résoudre l'équation de transfert du rayonnement et
traiter explicitement les différents mode de transport de
l'énergie.
résultant en principe d'un modèle décrivant l'atmosphère de
l'étoile. Un modèle détaillé d'atmosphère, absent du présent
modèle de structure interne, peut devenir nécessaire pour
résoudre l'équation de transfert du rayonnement et
traiter explicitement les différents mode de transport de
l'énergie.
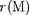 et L =
et L =
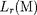 résulteront de la résolution des équations de structure
interne.
résulteront de la résolution des équations de structure
interne.
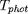 est identifiée à la température effective
est identifiée à la température effective
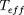 de l'étoile, c'est-à-dire à la température du corps noir de même
puissance par unité de surface :
de l'étoile, c'est-à-dire à la température du corps noir de même
puissance par unité de surface :
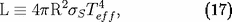
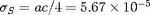 constante de Stefan).
constante de Stefan).
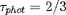 et donc que, en ordre de grandeur, compte tenu de (3) et
(9) :
et donc que, en ordre de grandeur, compte tenu de (3) et
(9) :
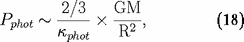
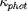 est l'opacité photosphérique. Cette expression fournit une
masse volumique
est l'opacité photosphérique. Cette expression fournit une
masse volumique
 .
.
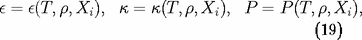
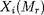 symbolise la composition chimique et isotopique.
symbolise la composition chimique et isotopique.
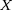 la masse d'hydrogène par unité de masse de matière
stellaire,
la masse d'hydrogène par unité de masse de matière
stellaire,
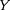 celle d'hélium et
celle d'hélium et
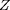 la somme de celles des autres éléments (surtout
C, N et O). Les valeurs rencontrées dans la photosphère
solaire (
la somme de celles des autres éléments (surtout
C, N et O). Les valeurs rencontrées dans la photosphère
solaire (
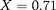 ,
,
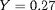 ,
,
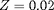 ) sont typiques de celles qu'aura une étoile de
composition encore homogène peu de temps après
sa formation (
) sont typiques de celles qu'aura une étoile de
composition encore homogène peu de temps après
sa formation (
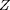 dépend cependant de la "population" d'étoiles
considérée).
dépend cependant de la "population" d'étoiles
considérée).
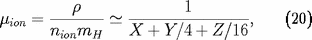
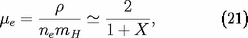
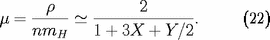
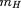 est la masse de l'atome d'hydrogène,
est la masse de l'atome d'hydrogène,
 la densités numérique totale de toutes les particules
libres,
la densités numérique totale de toutes les particules
libres,
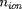 celle des ions et
celle des ions et
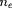 celle des électrons libres. Ces expressions de
celle des électrons libres. Ces expressions de
 et surtout de
et surtout de
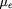 sont à modifier dans l'atmosphère des étoiles froides,
incomplètement ionisées.
sont à modifier dans l'atmosphère des étoiles froides,
incomplètement ionisées.
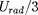 , donnée par (10), et de la pression gazeuse :
, donnée par (10), et de la pression gazeuse :
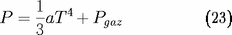
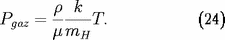
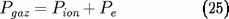
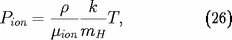
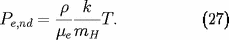
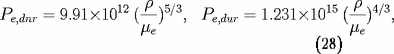
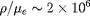 g/cm
g/cm
 . Une forme approchée de la pression de dégénérescence
est alors :
. Une forme approchée de la pression de dégénérescence
est alors :
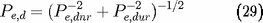
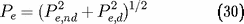
 est une moyenne harmonique de l'opacité monochromatique
est une moyenne harmonique de l'opacité monochromatique
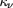 , pondérée par la dérivée de la fonction de Planck
, pondérée par la dérivée de la fonction de Planck
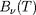 ("moyenne de Rosseland") :
("moyenne de Rosseland") :
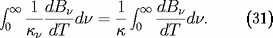
![ke = 0.20(1+X )[1+2.7 × 1011r/T 2]- 1[1+(T /4.5 × 108)0.86] - 1, (32)](images-TeX4ht/stellar90x.gif)
 et/ou
et/ou
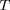 très élevées).
très élevées).
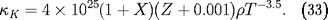
 , formé par recombinaison d'électrons libres issus de
métaux partiellement ionisés avec l'atome d'hydrogène,
ainsi que les molécules deviennent des absorbants
importants. En ordre de grandeur, on adopte
pour l'opacité du milieu dans le régime basse
température (d'autres sources d'opacité que
H
, formé par recombinaison d'électrons libres issus de
métaux partiellement ionisés avec l'atome d'hydrogène,
ainsi que les molécules deviennent des absorbants
importants. En ordre de grandeur, on adopte
pour l'opacité du milieu dans le régime basse
température (d'autres sources d'opacité que
H
 sont implicitement ajoutées vers 10
sont implicitement ajoutées vers 10
 K) :
K) :
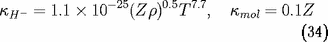
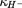 est utilisé harmoniquement).
est utilisé harmoniquement).
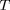 ) et peut donc être formellement représentée au moyen
d'une "opacité conductive", dont une expression
approchée est :
) et peut donc être formellement représentée au moyen
d'une "opacité conductive", dont une expression
approchée est :
![- 7 2 6 2/3 kcond = 2.6 × 10 (X +2Y +8Z )(T /r) [1+(r/2 × 10 ) ]. (35)](images-TeX4ht/stellar100x.gif)
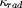 est alors effectué à l'aide de :
est alors effectué à l'aide de :
![1 1 k = k + [------ + -------------]- 1. (36) rad mol k - (k + k ) H e K](images-TeX4ht/stellar102x.gif)
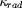 présente un maximum prononcé pour
présente un maximum prononcé pour
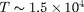 K (ionisation de l'hydrogène).
K (ionisation de l'hydrogène).
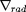 est :
est :
![1 1 k = [------+ -------]- 1. (37) krad kcond](images-TeX4ht/stellar106x.gif)
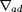 (équation 13) s'effectue directement à partir des
grandeurs thermodynamiques car
(équation 13) s'effectue directement à partir des
grandeurs thermodynamiques car
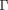 n'est pas connu a priori :
n'est pas connu a priori :
![@ ln(P ) @ ln(r) @ ln(P ) - 1 \~/ ad = [ ----------|s ----------|s + ----------|r ] . @ ln(r) @ ln(T ) @ ln(T ) (38)](images-TeX4ht/stellar109x.gif)
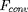 doit alors être calculé en détail en fonction des
caractéristiques du milieu et ajouté au flux
radiatif
doit alors être calculé en détail en fonction des
caractéristiques du milieu et ajouté au flux
radiatif
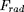 . La conservation du flux net impose :
. La conservation du flux net impose :
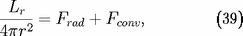
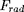 est encore obtenu à l'aide de l'expression (12)
est encore obtenu à l'aide de l'expression (12)
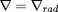 , mais dans laquelle
, mais dans laquelle
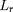 a été remplacée par
a été remplacée par
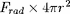 . Rappelons cependant que, dans les couches les plus
externes, les expression (12) et (31) elles-mêmes cessent
d'être précises.
. Rappelons cependant que, dans les couches les plus
externes, les expression (12) et (31) elles-mêmes cessent
d'être précises.
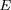 entre particules de charges
entre particules de charges
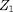 et
et
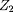 et de masse réduite
et de masse réduite
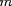 , la probabilité de traverser la barrière coulombienne
répulsive est
, la probabilité de traverser la barrière coulombienne
répulsive est
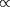 exp(
exp(
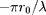 ), avec
), avec
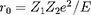 la distance d'approche classique et
la distance d'approche classique et
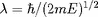 la longueur d'onde De Broglie. Pour une distribution
de Maxwell des noyaux, la probabilité de rencontrer
une paire d'énergie
la longueur d'onde De Broglie. Pour une distribution
de Maxwell des noyaux, la probabilité de rencontrer
une paire d'énergie
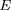 est
est
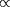 exp(
exp(
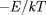 ). L'intégrale du produit de ces deux probabilités,
principal facteur dépendant de
). L'intégrale du produit de ces deux probabilités,
principal facteur dépendant de
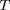 dans le taux de fusion, est
dans le taux de fusion, est
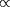 exp(
exp(
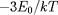 ), où
), où
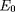 correspond au maximum de ce produit ("pic de
Gamow"). Le nombre de fusions /g/s est donné
par :
correspond au maximum de ce produit ("pic de
Gamow"). Le nombre de fusions /g/s est donné
par :
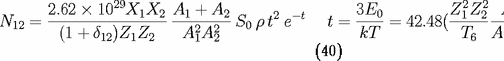
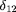 le symbole de Kronecker,
le symbole de Kronecker,
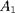 et
et
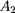 les poids atomiques,
les poids atomiques,
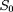 (en "kev-barn") la partie proprement nucléaire de la
section efficace et
(en "kev-barn") la partie proprement nucléaire de la
section efficace et
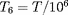 K. L'expression (40) est modifiée lorsque la section
nucléaire présente une résonance d'énergie voisine de
celle du pic de Gamow.
K. L'expression (40) est modifiée lorsque la section
nucléaire présente une résonance d'énergie voisine de
celle du pic de Gamow.
 H en noyaux
H en noyaux
 He s'effectue soit par des chaînes de réactions initiées
par la fusion proton-proton
He s'effectue soit par des chaînes de réactions initiées
par la fusion proton-proton
 H +
H +
 H
H
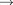
 H et impliquant seulement la fusion de protons avec
des sous-produits de cette fusion initiale ("chaînes
pp"), soit par des réactions dans lesquelles une
série d'isotopes de C, N et O jouent le rôle de
catalyseurs, globalement conservés au cours
de cycles successifs ("cycle CNO"). L'énergie
dégagée est d'environ 6.5 MeV par nucléon.
Les taux respectifs de production d'énergie
par unité de masse (en erg/s/g) sont donnés
par :
H et impliquant seulement la fusion de protons avec
des sous-produits de cette fusion initiale ("chaînes
pp"), soit par des réactions dans lesquelles une
série d'isotopes de C, N et O jouent le rôle de
catalyseurs, globalement conservés au cours
de cycles successifs ("cycle CNO"). L'énergie
dégagée est d'environ 6.5 MeV par nucléon.
Les taux respectifs de production d'énergie
par unité de masse (en erg/s/g) sont donnés
par :
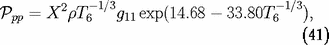
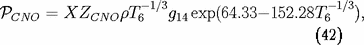
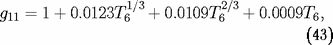
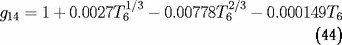
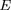 . La fraction de masse sous forme de CNO,
. La fraction de masse sous forme de CNO,
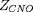 , vaut 2
, vaut 2
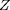 /3 dans le programme.
/3 dans le programme.
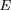 par
par
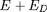 , avec
, avec
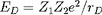 l'énergie de Debye (
l'énergie de Debye (
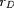 rayon de Debye), et donc à multiplier le taux de fusion
par le facteur d'écran :
rayon de Debye), et donc à multiplier le taux de fusion
par le facteur d'écran : 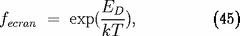
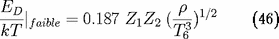
 élevée,
élevée,
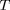 faible) :
faible) : ![ED 5/3 5/3 (r/me)1/3 -----|fort = 0.205 [(Z1+Z2)5/3 - Z 1 - Z 2 ]-------------. kT T6 (47)](images-TeX4ht/stellar159x.gif)
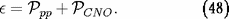
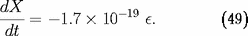
 He est
He est
 C, produisant environ 0.6 MeV par nucléon et exigeant
la fusion de trois particules
C, produisant environ 0.6 MeV par nucléon et exigeant
la fusion de trois particules
 , rendue possible par l'existence d'un noyau
métastable
, rendue possible par l'existence d'un noyau
métastable
 Be et d'une résonance
Be et d'une résonance
 C. Le taux de production d'énergie par fusion
3
C. Le taux de production d'énergie par fusion
3
 est, en fonction de
est, en fonction de
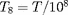 K :
K :
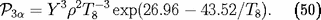
 C et
C et
 O) serait, à nouveau en g/s/g :
O) serait, à nouveau en g/s/g :
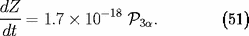
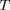 ,
,
 ,
,
 et
et
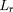 ayant une propension excessive à diverger aux
limites, il est interessant d'effectuer l'intégration
à la fois à partir de
ayant une propension excessive à diverger aux
limites, il est interessant d'effectuer l'intégration
à la fois à partir de
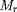 = 0 (vers l'extérieur) et de
= 0 (vers l'extérieur) et de
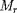 = M (vers l'intérieur) et de chercher par itération
à rendre les solutions continues en un point de
raccordement
= M (vers l'intérieur) et de chercher par itération
à rendre les solutions continues en un point de
raccordement
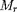 =
=
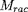 .
Les quatre paramètres de contour adoptés en pratique
sont, au centre, la température
.
Les quatre paramètres de contour adoptés en pratique
sont, au centre, la température
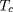 et la masse volumique
et la masse volumique
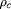 , à la surface, la température effective
, à la surface, la température effective
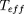 et la luminosité L (
et la luminosité L (
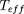 équivalente à R, moyennant (17)). L'intégration
peut être répétée en variant ces paramètres de tir,
ce qui permet d'évaluer la variation de l'écart sur
équivalente à R, moyennant (17)). L'intégration
peut être répétée en variant ces paramètres de tir,
ce qui permet d'évaluer la variation de l'écart sur
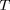 ,
,
 ,
,
 et
et
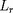 en
en
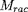 et d'améliorer ainsi le choix des paramètres de
contour pour l'itération suivante.
et d'améliorer ainsi le choix des paramètres de
contour pour l'itération suivante.
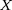 ,
,
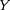 ) n'est plus homogène après
) n'est plus homogène après
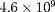 années d'évolution. Commentaire ? Commentez aussi la
variation des différentes variables avec la position : zone
de production d'énergie nucléaire, etc.
années d'évolution. Commentaire ? Commentez aussi la
variation des différentes variables avec la position : zone
de production d'énergie nucléaire, etc.
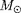 ou très inférieures à 0.5
ou très inférieures à 0.5
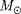 ? Explications ?
? Explications ?
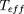 ) (
) (
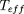 croissante vers la gauche). Reportez-y les résultats de
modèles d'étoiles déjà obtenus. Pour une composition solaire
uniforme, vous avez une représentation de la série principale
d'âge zéro (en anglais ZAMS pour "Zero Age Main Sequence").
croissante vers la gauche). Reportez-y les résultats de
modèles d'étoiles déjà obtenus. Pour une composition solaire
uniforme, vous avez une représentation de la série principale
d'âge zéro (en anglais ZAMS pour "Zero Age Main Sequence").
 Be,
Be,
 B, etc.), il devient par exemple possible de calculer un
spectre de neutrinos plus complet et de comparer les résultats
à ceux donnés dans les innombrables publications dédiées
au "mystère des neutrinos solaires".
B, etc.), il devient par exemple possible de calculer un
spectre de neutrinos plus complet et de comparer les résultats
à ceux donnés dans les innombrables publications dédiées
au "mystère des neutrinos solaires".
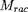 , la procédure Inward utilisant une composition modifiée
et la procédure Outward la composition habituelle. Le
sous-menu Composition pourrait être modifié pour afficher
cette nouvelle option. La valeur choisie pour
, la procédure Inward utilisant une composition modifiée
et la procédure Outward la composition habituelle. Le
sous-menu Composition pourrait être modifié pour afficher
cette nouvelle option. La valeur choisie pour
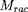 pourrait être motivée par des considérations sur la taille
de la zone convective centrale éventuelle des étoiles de la
ZAMS (voir plus haut).
pourrait être motivée par des considérations sur la taille
de la zone convective centrale éventuelle des étoiles de la
ZAMS (voir plus haut).
 en faisant appeler NuclearPowerAlpha par NuclearPower,
ce qui vous permet au moins d'étudier la ZAMS des étoiles
d'hélium pur. Plus ambitieux, vous pourriez vous intéresser
à des étoiles présentant un coeur d'hélium nucléairement
actif, entouré d'une enveloppe encore riche en hydrogène.
Notez que ces étoiles à coeur d'hélium continuent le plus
souvent à fusionner de l'hydrogène dans une couche fine
constituant la frontière du coeur, bien que l'une ou l'autre
source d'énergie puisse dominer selon les moments. Des
complications pourraient s'ensuivre...
en faisant appeler NuclearPowerAlpha par NuclearPower,
ce qui vous permet au moins d'étudier la ZAMS des étoiles
d'hélium pur. Plus ambitieux, vous pourriez vous intéresser
à des étoiles présentant un coeur d'hélium nucléairement
actif, entouré d'une enveloppe encore riche en hydrogène.
Notez que ces étoiles à coeur d'hélium continuent le plus
souvent à fusionner de l'hydrogène dans une couche fine
constituant la frontière du coeur, bien que l'une ou l'autre
source d'énergie puisse dominer selon les moments. Des
complications pourraient s'ensuivre...
 ! Les résultats sont-ils très surprenants ? Commentez,
notamment selon la valeur de M. Vous pouvez de même
modifier ou supprimer tel ou tel terme de la loi d'opacité,
ou encore tester l'influence de la valeur de la constante de
la gravitation
! Les résultats sont-ils très surprenants ? Commentez,
notamment selon la valeur de M. Vous pouvez de même
modifier ou supprimer tel ou tel terme de la loi d'opacité,
ou encore tester l'influence de la valeur de la constante de
la gravitation
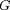 . L'altération des constantes physiques fondamentales, pour
être introduite de manière cohérente, peut vous amener à
remonter à l'expression littérale de coefficients numériques
contenant implicitement ces constantes.
. L'altération des constantes physiques fondamentales, pour
être introduite de manière cohérente, peut vous amener à
remonter à l'expression littérale de coefficients numériques
contenant implicitement ces constantes.

