Simulation du modèle d'Ising
Auteurs:
Dounia Saez, Clément Perrot, Léo Vandamme
Date de création :
3 octobre 2012
Date de mise à jour :
13 décembre 2012
Table des matières
Liste des paramètres d'entrée de l'applet
-
titre : Nombre de lignes
label : nlignes
Nombre de lignes pour les grilles carrée et hexagonale
-
titre : Nombre de colonnes
label : ncolonnes
Nombre de colonnes pour les grilles carrée et hexagonale
-
titre : Grossissement
label : gamma
Grossissement visuel de la grille de spins
-
titre : Nombre de boucles
label : nboucle
Nombre de changements d'état du système à une T donnée, utilisé pour atteindre l'équilibre du système
Pour des valeurs significatives en mode calcul, lancer au moins 10 000 000 boucles
En mode visuel, on réalise nlignes*ncolonnes boucles pour un temps de calcul réduit.
-
titre : Nombre de sous boucles
label : nsousboucle
Nombre de fois où le système se trouve à l'état d'équilibre, utilisé pour calculer les valeurs de l'énergie et de l'aimantation
Pour des valeurs significatives en mode calcul, lancer au moins 100 sous boucles.
En mode visuel, on réalise une seule boucle pour un temps de calcul réduit.
-
titre : Choix de la grille
label : gtype
Sélectionne le type de grille
Valeurs possibles :
Grille carrée
Grille Hexagonale
-
titre : h_ext
label : hext
Valeur du champ magnétique externe
-
titre : deltaT
label : dt
Incrémentation dt de la température à chaque itération
-
titre : Température de départ
label : temperature
Température de départ du système, dans le cas où elle est fixée (mode Visuel).
La température de départ vaut 0.1 en cas d'évolution de la température (mode Calcul).
Température critique ~ 2.27
Liste des paramètres de sortie de l'applet
-
label : grille
-
titre : Nombre de flip-spin
label : ns
-
titre : Température
label : temperature
-
titre : E
label : etot
-
titre : M
label : M
-
titre : Corrélation moy
label : moyenne
-
titre : Taille du motif
label : nbmotif
unités : pixels
Champ
Modélisation du modèle d'Ising à 2 dimensions
Introduction
Dans ce projet, nous allons étudier le modèle d'Ising à deux dimensions, particulièrement la transition de phase.
Le modèle d'Ising permet l'étude du comportement de N particules ponctuelles à un degré de liberté qui intéragissent localement. Nous supposerons ici que ces particules sont des spins pouvant être dans l'état + ou -, et qu'elles intéragissent seulement avec leurs premiers voisins, dont le nombre est déterminé par le type de grille 2D.
Nous traiterons donc le problème comme un problème de physique statistique dans un cadre canonique, où notre système baigne dans un champ magnétique constant, et où les spins sont discernables.
Objectifs
Cette applet va permettre de déterminer la température de la transition de phase selon 2 paramètres:
- L'organisation des spins dans le plan (grille)
- Le sens et l'intensité du champ magnétique (en réalité ce paramètre est rapporté à l'énergie de liaison)
Explications
Instruction des différents ensembles pour l'utilisation de l'Applet
Visuel : grille carrée avant Tc
A lancer en mode visuel, avec ou sans champ magnétique extérieur. Utilise une grille carrée de 100 par 100, à température fixée avant la température critique.
Visuel : grille carrée à Tc
A lancer en mode visuel, avec ou sans champ magnétique extérieur. Utilise une grille carrée de 100 par 100, à température fixée à la température critique.
Visuel : grille carrée après Tc
A lancer en mode visuel, avec ou sans champ magnétique extérieur. Utilise une grille carrée de 100 par 100, à température fixée après la température critique.
Visuel : grille hexa avant Tc
A lancer en mode visuel, avec ou sans champ magnétique extérieur. Utilise une grille hexagonale de 100 par 100, à température fixée avant la température critique.
Visuel : grille hexa à Tc
A lancer en mode visuel, avec ou sans champ magnétique extérieur. Utilise une grille hexagonale de 100 par 100, à température fixée à la température critique.
Visuel : grille hexa après Tc
A lancer en mode visuel, avec ou sans champ magnétique extérieur. Utilise une grille hexagonale de 100 par 100, à température fixée après la température critique.
Calcul lourd : grille carrée
A lancer en mode calcul, avec ou sans champ magnétique extérieur. Utilise une grille carrée de 100 par 100, à température variable, partant de 0.5 et augmentant de 0.005. Le nombre d'itération pour chaque température est de 5 000 000 effectuées 50 fois. Attention, l'évolution est très lente !
Calcul leger : grille carrée
A lancer en mode calcul, avec ou sans champ magnétique extérieur. Utilise une grille carrée de 100 par 100, à température variable, partant de 0.5 et augmentant de 0.01. Le nombre d'itération pour chaque température est de 20 000 effectuées 40 fois. L'évolution est rapide et permet d'obtenir des courbes d'énergie et d'aimantation en fonction de la température assez rapidement. (contrairement au mode "lourd")
Calcul lourd : grille hexa
A lancer en mode calcul, avec ou sans champ magnétique extérieur. Utilise une grille hexagonale de 100 par 100, à température variable, partant de 1.5 et augmentant de 0.005. Le nombre d'itération pour chaque température est de 5 000 000 effectuées 50 fois. Attention, l'évolution est très lente !
Calcul leger : grille carrée
A lancer en mode calcul, avec ou sans champ magnétique extérieur. Utilise une grille hexagonale de 100 par 100, à température variable, partant de 1.5 et augmentant de 0.01. Le nombre d'itération pour chaque température est de 20 000 effectuées 40 fois. L'évolution est rapide et permet d'obtenir des courbes d'énergie et d'aimantation en fonction de la température assez rapidement. (contrairement au mode "lourd")
Explications
Généralités sur le modèle d'Ising
Le modèle d'Ising consiste à mettre sur un réseau le moment magnétique de N particules, tous alignés sur le même axe.
Chaque moment magnétique peut donc prendre deux directions, que l'on note + et -.
Ces spins intéragissent avec leurs voisins, et souvent, on considère qu'ils intéragissent seulement
avec les voisins les plus proches. Dans le cas du modèle d'Ising à deux dimensions, il à été montré par Rudolf Peierls qu'il existe une transition entre une phase ordonnée: le champ magnétique total du réseau est différent de 0, ce qui signifie que les + et - ont tendances à se regrouper, et une phase désordonnée où l'aimentation est nulle.
Énergie du réseau
On écrit, pour une configuration quelconque des spin, i.e d'un état
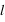
, l'énergie totale du réseau dans le cas général:
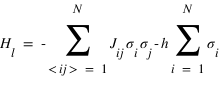
que l'on simplifiera
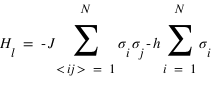
où
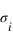
prend la valeur +1 ou -1 (orientation du spin),
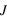
désigne l'énergie d'intéraction entre 2 spins premiers voisins,
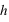
l'énergie du champ magnétique externe et
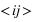
signifie que l'on prend la somme sur les premiers voisins. On s'intéressera dans toute la suite au cas où
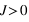
; c'est à dire où les intéractions entre spins sont ferromagnétiques.
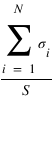
désigne l'aimantation moyenne par spin du système (S = surface du réseau).
Dans le modèle d'Ising 2D, il existe une transition de phase du second ordre à la température critique (ou température de Curie) notée
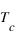
. Celle-ci est définie comme étant la température au voisinage de laquelle le système le système n'est ni ordonné, ni désordonné.
La solution exacte d'Onsager donne, pour la température critique la valeur théorique
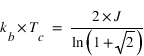
soit
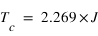
.
Les différentes constantes physiques que l'on peut calculer se comportent différemment au voisinage
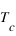
.
- Aimentation : derivée 1ère de l'énergie, continue
- Entropie : derivée 1ère de l'énergie, continue
- Chaleur spécifique : derivée 2nde de l'énergie, discontinue
- Susceptibilité : derivée 2nde de l'énergie, discontinue
Les exposants critiques caractérisent les comportements universels des lois physiques dans le cas de systèmes possédant une transition de phase du second ordre.
- Aimentation :
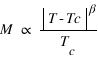 ,
, 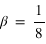
- Chaleur spécifique :
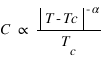 ,
, 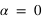
- Susceptibilité :
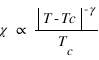 ,
, 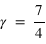
- Longueur de corrélation :
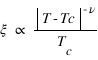 ,
, 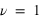
Algorithme de Métropolis
A température fixée, le système doit à priori converger vers un état d'équilibre. Il faut donc un algorithme permettant de modéliser convenablement l'évolution du système.
Rappelons que la probabilité que le système soit, à l'équilibre, dans un état
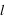
à température fixée est donnée par
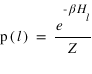
, où
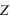
est la fonction de partion du système à
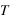
et
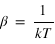
Le principe ergodique stipule que sur un temps d'évolution suffisament long, le système doit converger vers son état d'équilibre le plus probable.
Le but est donc de faire en sorte que le système tende vers cet état.
L'algorithme consiste à retourner un spin
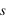
au hasard dans le réseau, et de donner un critère d'acceptation du nouvel état
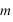
. Le critère est le suivant:
On pose
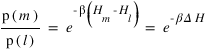
1er cas: Si
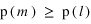
, soit
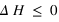
alors le nouvel état est accepté, le
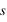
reste dans son nouvel état.
2ème cas: Si
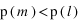
, soit
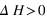
la probabilité que le nouvel état soit accepté est
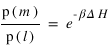
On recomence l'expérience autant de fois que necessaire pour atteindre l'état d'équilibre, et ceci nous donne un bon modèle de l'évolution de notre système.
Cette méthode est très commode car le calcul de
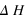
ne nécessite pas de calculer
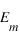
et
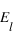
, on peut calculer juste la variation d'énergie du sous système {
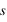 + premiers voisins
+ premiers voisins}, ce qui allège considérablement le temps de calcul.
L'algorithme nous donne déjà une bonne idée sur l'évolution du système en fonction de la température. En effet, à haute température,
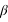
tend vers 0, donc
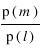
tend vers 1, les états d'équilibre tendent à être équiprobable. Le système est en phase désordonnée.
En revanche à température faible, si
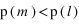
, la probabilité que le nouvel état soit accepté est très faible, le système converge donc vite vers l'équilibre.
On peut sentir que, au voisinage d'une certaine température, le système cherche à converger à cause du 1er cas, mais que la probabilité d'acceptation 2ème cas n'est pas suffisament faible pour le permettre.
Évolution du du modèle d'Ising en fonction de la température
Dans ce modèle, pour étudier l'évolution d'une quantité physique
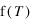
en fonction de la température , il faudrait dans l'idéal que pour chaque T le système soit à l'équilibre.
Mais on peut prévoir que s'il existe une température
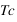
à laquelle le système n'arrive jamais à l'équilibre, le temps de relaxation au voisinage de cette température diverge.
L'inconvénient majeur des simulations est que si on veut des résultats convenables, pour toutes les valeurs de température que l'on considère il faut faire évoluer le système sur un temps très long, ce qui revient à itérer sur beaucoup de boucles l'algorithme de Métropolis.
Mode d'emploi de l'applet
Description des paramètres
Taille de la grille
Le choix de la taille de la grille (npoints, nlignes, ncolonnes) permet à l'utilisateur de choisir entre un réseau contenant beaucoup de spins mais qui mettera plus de temps à converger vers l'état d'équilibre, ou un petit réseau moins réaliste mais plus commode à étudier.
Grossissement
Permet d'agrandir visuellement le réseau de spins.
Mode calcul ou mode visuel
Le mode visuel permet d'observer l'évolution du système à une température fixée.
Le mode calcul donne l'énergie totale, l' aimantatation et la fonction de correlation en fonction de la température.
nboucles
N'intervient que dans le mode "calcul". Nboucle correspond à la durée dont on souhaite faire évoluer le système avant de l'évaluer. Il exprime en réalité le nombre tests effectués sur le réseau avant de calculer les énergies.
En mode "visuel", ce nombre est fixé à nlignes*ncolonnes.
nsousboucle
N'intervient aussi que dans le mode "calcul". Pour que nos résultats soient plus fiables, on calcule plusieur fois l'énergie et l'aimantation, pour ne garder que la moyenne. Ce paramètre permet de definir sur combien de mesures on souhaite faire la moyenne.
Remarque :
En mode "Calcul", le nombre de tests effectués sur le réseau entre deux affichages est donc de
nboucles * nsousboucles.
hext
Intensité et sens (selon le signe) du champ magnétique dans lequel baigne le réseau.
Choix des unités
Les trois seules quantités physiques qui vont apparaîtres dans notre problème sont l'énergie, la température et la constante de Boltzmann
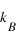
, qui s'exprime en Joule/Kelvin. On peut toujours redéfinir le joule ou le kelvin (ou les 2) de manière à ce que
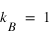
.
On fixe, dans toutes les simulations, l'énergie de liaison à
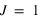
.
Les paramètres
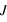
,
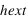
(h) et
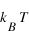
(T) sont considérés dédimensionnés, car on ne s'intéresse qu'a leur valeur relative.
Les valeurs affichées sont des valeurs moyenne par spin. L'énergie totale et l'aimantation sont normalisées à 1.
Exemple
Évolution temporelle du système pour une grille carrée à 4 températures différentes et h=0.
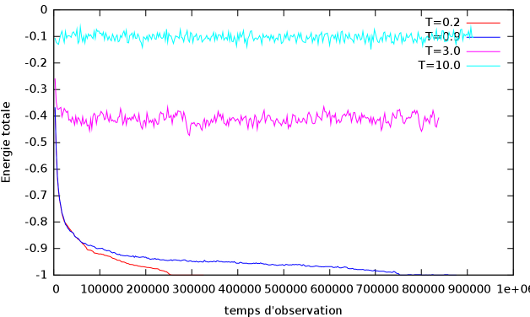
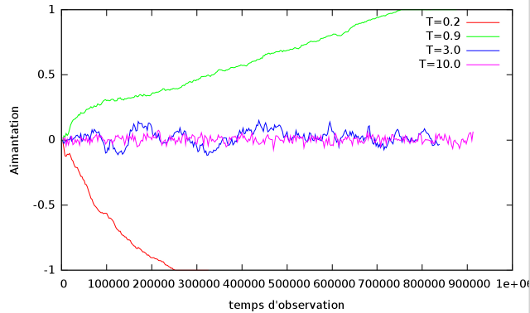
Courbe représentant l'évolution temporelle de l'énergie totale et de l'aimantation du réseau du système à T=0, T=0.9, T=3.0, T=10.0
Le temps d'observations correspond au nombre de tests effectués sur le réseau.
Remarque :
On remarque que pour des températures très faibles, le système converge complètement vers un des 2 états d'énergie minimum (que des + ou que des -), ce qui explique pourquoi l'aimantation converge soit vers +1 soit vers -1. On voit que dans cette phase, le temps de relaxation croît avec la température. Dans cette phase,
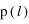
est donc maximum seulement pour ces 2 états.
En revanche, à température suffisament élevée, l'énergie fluctue autour d'une valeur moyenne. Il existe apparament plusieurs états
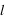
pour lesquels
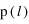
est maximum. Cette valeur moyenne semble s'approcher de 0 quand la température augmente (état équiprobables ⇒ énergie moyenne nulle).
Exemple
Évolution temporelle du champ magnétique du réseau à température faible (T=0.2) avec trois valeurs du champ externe pour la grille carrée.
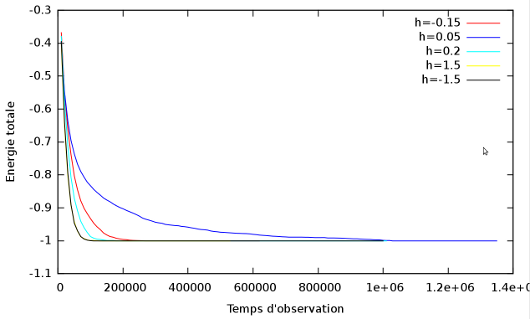
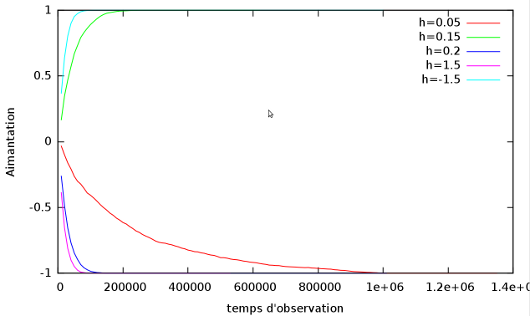
Comportement de l'énergie totale et de l'aimantation à T=0 pour différentes valeurs du champs magnétiques externe 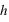 .
.
Remarque :
On voit que l'intensité du champ à tendance à diminuer le temps de relaxation, et que le sens du champ favorise l'état {+} ou {-} (
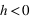
favorise l'état {+} et
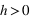
favorise l'état {-}) .
Exemple
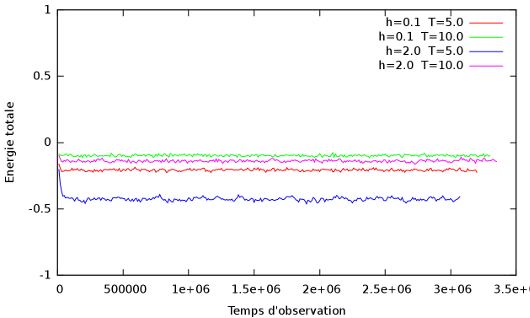
Évolution temporelle de l'énergie totale du réseau à haute température (T=5.0 et T=10.0) avec trois valeurs du champ externe pour la grille carrée.
Remarque :
On voit qu'à haute température, le champ magnétique à tendance à diminuer l'énergie moyenne du système. Mais cet effet est concurencé par la valeur de la température, puisqu'on voit que pour une même valeur de
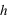
, l'énergie moyenne du système se rapproche de zéro quand la température augmente.
L'évolution temporelle du réseau nous donne déjà une bonne idée du comportement du système selon la phase dans laquelle il se trouve. Mais pour déterminer précisément la transition de phase, il faut observer l'évolution en température du système.
Dans les résultats qui suivent, nous initialisons le réseau dans l'état {+} pour la température de départ. Cela nous permet d'éviter les problèmes liés à la périodicité. A température
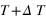
, l'état initial du réseau est l'état final du réseau à la température
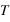
. Pour chaque point, le système à évolué de 10000 tests et les valeurs sont moyennées sur 50 mesures. Rappelon l'état {+} est l'état vers lequel converge le système quand
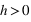
à faible température.
Exemple
Évolution de l'énergie totale et de l'aimantation en fonction de la température. La grille est carrée et il n'y a pas de champ externe.
Remarque :
La courbe d'aimantation montre bien la transition de phase. On estime la température critique aux alentours de 2.45 dans ce cas. La solution analytique de Onsager donne une température de 2.27.
Exemple
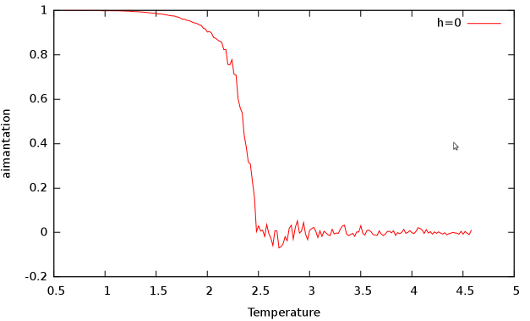
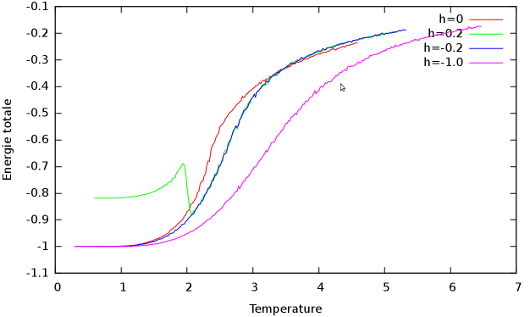
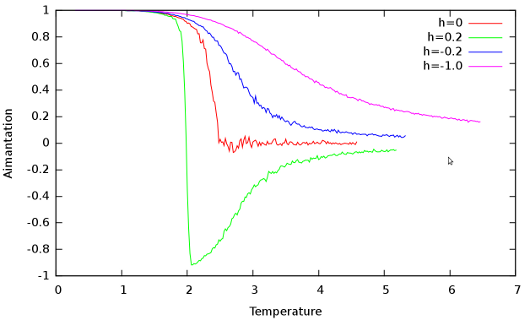
Même conditions que précédemment mais avec un champ externe non nul.
Remarque :
On voit que pour
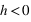
, la transition de phase est beaucoup plus amortie que sans champ externe. Cet effet est croissant avec l'intensité de h.
Pour
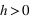
, le système passe soudainement de l'état {+} à l'état {-} autour d'une température d'environ 2.0. Ceci est dû au fait que nous avons initialisé la grille dans l'état {+}. En effet, à trop basse température, le champ magnétique n'est pas assez fort pour faire basculer le système, mais dès que la température est suffisante, le champ externe pousse très violement le système dans l'état où il devrait être si l'initialisation était aléatoire.
Une fois connue la température de la transition de phase, il est intéressant d'observer l'évolution temporelle du système à cette température.
Exemple
Aimantation en fonction du temps d'observation à
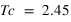
. Le champ externe est nul.
Remarque :
On constate qu'à cette température, le comportement de l'aimantation est très aléatoire. Il ne converge pas vers un des états {+} ou {-}, et n'oscille vers aucune valeur particulière.
Taille caractéristique du système
La taille caractérisique du système correspond à la taille typique d'un groupe de cellules de même spin.
Afin de déterminer cette taille on calcule les coefficients de corrélation du système.
Pour cela on va définir des boites carrées dont la taille varie de trois cellules de côté à toute la taille de la grille. Le but est
de faire défiler ces boites sur toute la grille sans qu'il y ait de recouvrement.
A l'intérieur de chaque boite on compare l'état des spins avec l'état du spin central test. Si tous les spins sont dans le même état, le coefficient de correlation vaut 1, si il y a autant de spins +1 que -1 alors le coefficient vaut 0 (il n'y a pas de correlation entre les spins). Faire défiler la boite le long de la grille nous permet d'avoir un coefficient de corrélation moyenné. Plus la taille du motif sera grande et plus on détectera des groupes de spin important.
Le coefficient de corrélation en fonction de la taille des motifs est donné par :
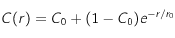
où r est la taille du motif,
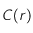
est la fonction de corrélation,
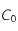
est la valeur asymptotique de la fonction de corrélation quand r augmente et
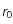
est la taille caratéristique.
Exemple
Correlation a T = 2,29
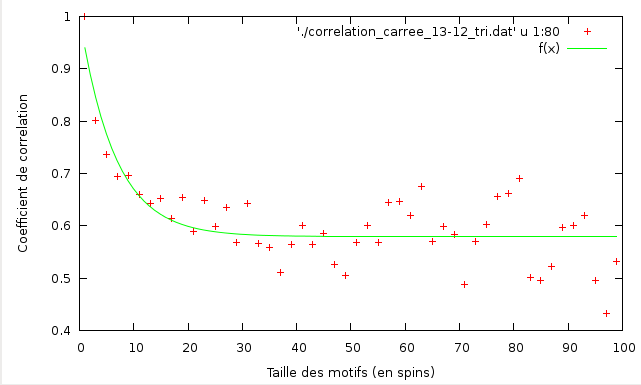
Ci-dessus la fonction de correlation pour T = 2.29 d'une grille carrée 100x100 sans champ magnétique extérieur.
On trouve
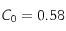
et
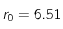
Correlation a T = 2,49
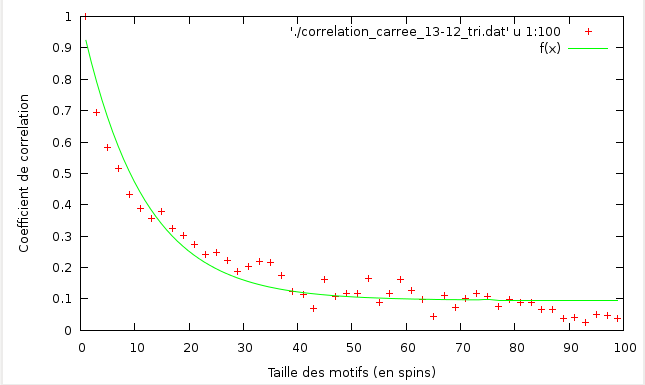
Ci-dessus la fonction de correlation pour T = 2.49 d'une grille carrée 100x100 sans champ magnétique extérieur.
On trouve
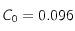
et
Correlation a T = 3,49
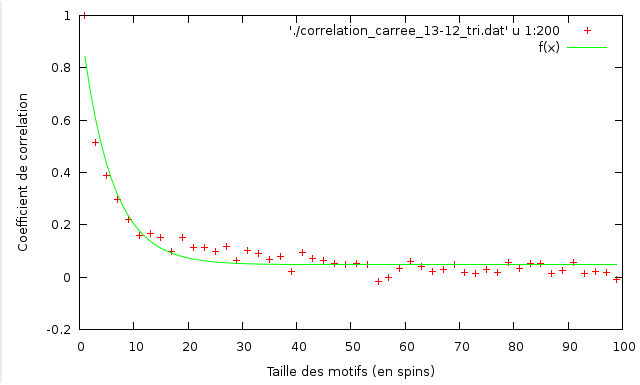
Ci-dessus la fonction de correlation pour T = 3.49 d'une grille carrée 100x100 sans champ magnétique extérieur.
On trouve
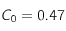
et
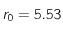
Correlation a T = 5.48
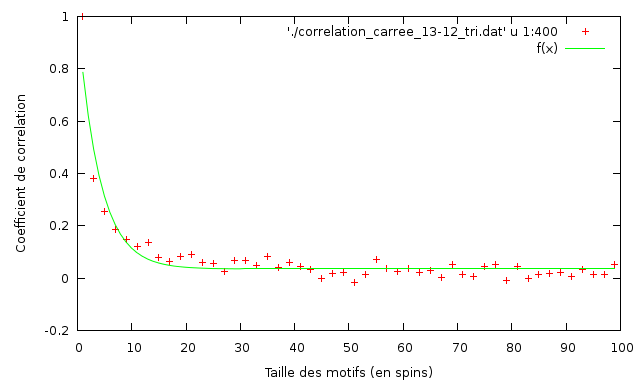
Ci-dessus la fonction de correlation pour T = 5.48 d'une grille carrée 100x100 sans champ magnétique extérieur.
On trouve
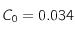
et
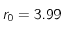
Les tailles caratéristiques donnent une indication de l'état du système dans le diagramme de phase, en effet à la température de Curie la taille caratéristique diverge, puis elle diminue lorsque la température augmente, c'est donc un moyen pour déterminer la température de Curie.
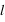 , l'énergie totale du réseau dans le cas général:
, l'énergie totale du réseau dans le cas général: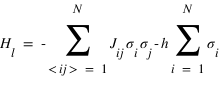
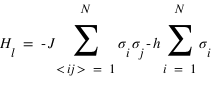
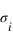 prend la valeur +1 ou -1 (orientation du spin),
prend la valeur +1 ou -1 (orientation du spin), 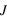 désigne l'énergie d'intéraction entre 2 spins premiers voisins,
désigne l'énergie d'intéraction entre 2 spins premiers voisins, 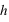 l'énergie du champ magnétique externe et
l'énergie du champ magnétique externe et 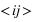 signifie que l'on prend la somme sur les premiers voisins. On s'intéressera dans toute la suite au cas où
signifie que l'on prend la somme sur les premiers voisins. On s'intéressera dans toute la suite au cas où 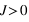 ; c'est à dire où les intéractions entre spins sont ferromagnétiques.
; c'est à dire où les intéractions entre spins sont ferromagnétiques.
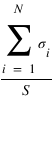 désigne l'aimantation moyenne par spin du système (S = surface du réseau).
désigne l'aimantation moyenne par spin du système (S = surface du réseau).
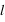 , l'énergie totale du réseau dans le cas général:
, l'énergie totale du réseau dans le cas général: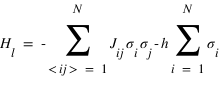
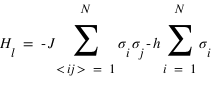
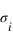 prend la valeur +1 ou -1 (orientation du spin),
prend la valeur +1 ou -1 (orientation du spin), 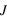 désigne l'énergie d'intéraction entre 2 spins premiers voisins,
désigne l'énergie d'intéraction entre 2 spins premiers voisins, 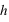 l'énergie du champ magnétique externe et
l'énergie du champ magnétique externe et 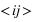 signifie que l'on prend la somme sur les premiers voisins. On s'intéressera dans toute la suite au cas où
signifie que l'on prend la somme sur les premiers voisins. On s'intéressera dans toute la suite au cas où 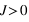 ; c'est à dire où les intéractions entre spins sont ferromagnétiques.
; c'est à dire où les intéractions entre spins sont ferromagnétiques.
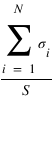 désigne l'aimantation moyenne par spin du système (S = surface du réseau).
désigne l'aimantation moyenne par spin du système (S = surface du réseau).
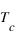 . Celle-ci est définie comme étant la température au voisinage de laquelle le système le système n'est ni ordonné, ni désordonné.
La solution exacte d'Onsager donne, pour la température critique la valeur théorique
. Celle-ci est définie comme étant la température au voisinage de laquelle le système le système n'est ni ordonné, ni désordonné.
La solution exacte d'Onsager donne, pour la température critique la valeur théorique 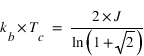 soit
soit 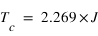 .
.
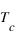 . Celle-ci est définie comme étant la température au voisinage de laquelle le système le système n'est ni ordonné, ni désordonné.
La solution exacte d'Onsager donne, pour la température critique la valeur théorique
. Celle-ci est définie comme étant la température au voisinage de laquelle le système le système n'est ni ordonné, ni désordonné.
La solution exacte d'Onsager donne, pour la température critique la valeur théorique 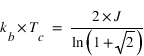 soit
soit 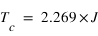 .
.
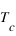 .
.
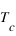 .
.
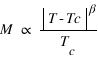 ,
, 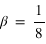
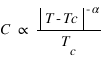 ,
, 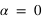
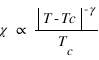 ,
, 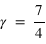
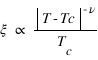 ,
, 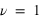
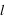 à température fixée est donnée par
à température fixée est donnée par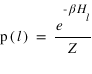 , où
, où 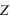 est la fonction de partion du système à
est la fonction de partion du système à 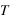 et
et 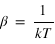
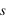 au hasard dans le réseau, et de donner un critère d'acceptation du nouvel état
au hasard dans le réseau, et de donner un critère d'acceptation du nouvel état 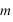 . Le critère est le suivant:
. Le critère est le suivant: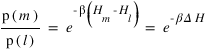
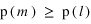 , soit
, soit 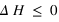 alors le nouvel état est accepté, le
alors le nouvel état est accepté, le 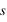 reste dans son nouvel état.
reste dans son nouvel état.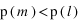 , soit
, soit 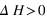 la probabilité que le nouvel état soit accepté est
la probabilité que le nouvel état soit accepté est 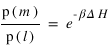
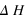 ne nécessite pas de calculer
ne nécessite pas de calculer 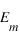 et
et 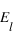 , on peut calculer juste la variation d'énergie du sous système {
, on peut calculer juste la variation d'énergie du sous système {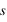 + premiers voisins}, ce qui allège considérablement le temps de calcul.
+ premiers voisins}, ce qui allège considérablement le temps de calcul.
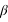 tend vers 0, donc
tend vers 0, donc 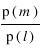 tend vers 1, les états d'équilibre tendent à être équiprobable. Le système est en phase désordonnée.
tend vers 1, les états d'équilibre tendent à être équiprobable. Le système est en phase désordonnée. 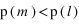 , la probabilité que le nouvel état soit accepté est très faible, le système converge donc vite vers l'équilibre.
, la probabilité que le nouvel état soit accepté est très faible, le système converge donc vite vers l'équilibre.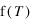 en fonction de la température , il faudrait dans l'idéal que pour chaque T le système soit à l'équilibre.
en fonction de la température , il faudrait dans l'idéal que pour chaque T le système soit à l'équilibre.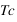 à laquelle le système n'arrive jamais à l'équilibre, le temps de relaxation au voisinage de cette température diverge.
à laquelle le système n'arrive jamais à l'équilibre, le temps de relaxation au voisinage de cette température diverge.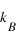 , qui s'exprime en Joule/Kelvin. On peut toujours redéfinir le joule ou le kelvin (ou les 2) de manière à ce que
, qui s'exprime en Joule/Kelvin. On peut toujours redéfinir le joule ou le kelvin (ou les 2) de manière à ce que 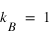 .
.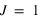 .
Les paramètres
.
Les paramètres 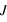 ,
, 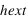 (h) et
(h) et 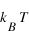 (T) sont considérés dédimensionnés, car on ne s'intéresse qu'a leur valeur relative.
(T) sont considérés dédimensionnés, car on ne s'intéresse qu'a leur valeur relative.

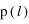 est donc maximum seulement pour ces 2 états.
est donc maximum seulement pour ces 2 états.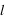 pour lesquels
pour lesquels 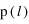 est maximum. Cette valeur moyenne semble s'approcher de 0 quand la température augmente (état équiprobables ⇒ énergie moyenne nulle).
est maximum. Cette valeur moyenne semble s'approcher de 0 quand la température augmente (état équiprobables ⇒ énergie moyenne nulle).


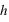 .
.
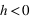 favorise l'état {+} et
favorise l'état {+} et 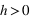 favorise l'état {-}) .
favorise l'état {-}) .
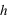 , l'énergie moyenne du système se rapproche de zéro quand la température augmente.
, l'énergie moyenne du système se rapproche de zéro quand la température augmente.
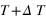 , l'état initial du réseau est l'état final du réseau à la température
, l'état initial du réseau est l'état final du réseau à la température 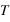 . Pour chaque point, le système à évolué de 10000 tests et les valeurs sont moyennées sur 50 mesures. Rappelon l'état {+} est l'état vers lequel converge le système quand
. Pour chaque point, le système à évolué de 10000 tests et les valeurs sont moyennées sur 50 mesures. Rappelon l'état {+} est l'état vers lequel converge le système quand 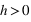 à faible température.
à faible température.

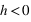 , la transition de phase est beaucoup plus amortie que sans champ externe. Cet effet est croissant avec l'intensité de h.
, la transition de phase est beaucoup plus amortie que sans champ externe. Cet effet est croissant avec l'intensité de h.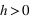 , le système passe soudainement de l'état {+} à l'état {-} autour d'une température d'environ 2.0. Ceci est dû au fait que nous avons initialisé la grille dans l'état {+}. En effet, à trop basse température, le champ magnétique n'est pas assez fort pour faire basculer le système, mais dès que la température est suffisante, le champ externe pousse très violement le système dans l'état où il devrait être si l'initialisation était aléatoire.
, le système passe soudainement de l'état {+} à l'état {-} autour d'une température d'environ 2.0. Ceci est dû au fait que nous avons initialisé la grille dans l'état {+}. En effet, à trop basse température, le champ magnétique n'est pas assez fort pour faire basculer le système, mais dès que la température est suffisante, le champ externe pousse très violement le système dans l'état où il devrait être si l'initialisation était aléatoire.
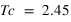 . Le champ externe est nul.
. Le champ externe est nul.
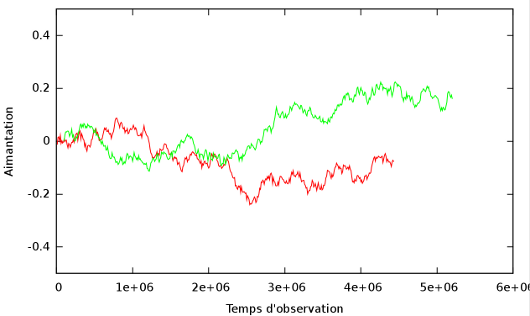
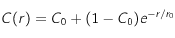 où r est la taille du motif,
où r est la taille du motif, 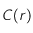 est la fonction de corrélation,
est la fonction de corrélation, 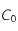 est la valeur asymptotique de la fonction de corrélation quand r augmente et
est la valeur asymptotique de la fonction de corrélation quand r augmente et 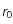 est la taille caratéristique.
est la taille caratéristique.

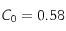 et
et 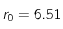

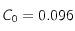 et
et 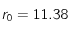

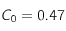 et
et 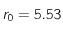

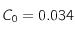 et
et 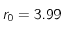 Les tailles caratéristiques donnent une indication de l'état du système dans le diagramme de phase, en effet à la température de Curie la taille caratéristique diverge, puis elle diminue lorsque la température augmente, c'est donc un moyen pour déterminer la température de Curie.
Les tailles caratéristiques donnent une indication de l'état du système dans le diagramme de phase, en effet à la température de Curie la taille caratéristique diverge, puis elle diminue lorsque la température augmente, c'est donc un moyen pour déterminer la température de Curie.