Introduction
Soit un ensemble de n points dans le plan, également appelés sites. Il existe bien des manières de diviser ce plan. Une des plus utilisées est appelée le diagramme de Voronoi. Elle subdivise le plan de la manière suivante : à chaque site P correspond une et une seule cellule V(P) telle que l'ensemble des points du plan ayant pour plus proche site P se situent dans la région V(P) appelée cellule.
Cette caractérisation, très intuitive, permet bien de "sentir" ce qu'est le diagramme de Voronoi. Malheureusement, cette méthode est assez compliquée à implémenter. Pour cette raison, nous allons utiliser une autre manière, équivalente au diagramme de Voronoi, de subdiviser le plan : la triangulation de Delaunay. Cette méthode est entièrement équivalente (cf section suivante).
Nous commencerons donc par présenter le maillage de Delaunay de manière théorique. Puis nous énoncerons certaines de ses propriétés et expliquerons son implémentation. Enfin, nous généraliserons cette méthode au maillage d'une sphère.
Equivalence entre le diagramme de Voronoi et le maillage de Delaunay
Comme nous l'avons dit auparavant, le maillage de Delaunay est rigoureusement équivalent au diagramme de Voronoi. En effet, il en constitue le dual. La dualité mathématique est une notion très complexe. Néanmoins, il est possible d'en donner une première approche intuitive.
Plaçons nous donc dans l'espace à 2 dimensions usuel. Soient O,A,B,C,D 5 sites (ou points du plan).
De Voronoi à Delaunay : supposons la cellule V(O) construite. Un point M du plan est voisin de O si et seulement si V(O) et V(M) ont une frontière commune. La connaissance des frontières de la cellule nous permet ainsi de connaître les voisins d'un site. On peut tracer les arêtes entre sites voisins et définir donc le maillage de Delaunay.
De Delaunay à Voronoi : supposons les arêtes entre O et ses voisins construits. On trace le polygone dont les sommets sont les points d'intersection des médiatrices de 2 arêtes consécutives. On définit ainsi de manière non ambiguë la cellule V(O), et donc le diagramme de Voronoi.
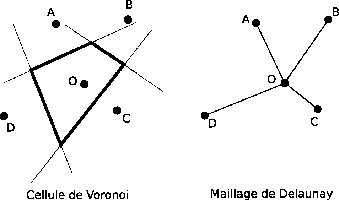
Cet exemple illustre très bien le concept de dualité. Connaître la cellule et ses frontières est rigoureusement équivalent à connaître les sites et les arêtes. Le diagramme de Voronoi et la maillage de Delaunay sont donc dits duals.
Plaçons nous donc dans l'espace à 2 dimensions usuel. Soient O,A,B,C,D 5 sites (ou points du plan).
De Voronoi à Delaunay : supposons la cellule V(O) construite. Un point M du plan est voisin de O si et seulement si V(O) et V(M) ont une frontière commune. La connaissance des frontières de la cellule nous permet ainsi de connaître les voisins d'un site. On peut tracer les arêtes entre sites voisins et définir donc le maillage de Delaunay.
De Delaunay à Voronoi : supposons les arêtes entre O et ses voisins construits. On trace le polygone dont les sommets sont les points d'intersection des médiatrices de 2 arêtes consécutives. On définit ainsi de manière non ambiguë la cellule V(O), et donc le diagramme de Voronoi.

Cet exemple illustre très bien le concept de dualité. Connaître la cellule et ses frontières est rigoureusement équivalent à connaître les sites et les arêtes. Le diagramme de Voronoi et la maillage de Delaunay sont donc dits duals.
Propriétés du maillage de Delaunay
Comme nous en avons donné un exemple auparavant, il est possible de construire le maillage de Delaunay à partir du diagramme de Voronoi. En effet, le maillage de Delaunay est un graphe dont les noeuds sont les sites P des cellules de Voronoi V(P) et les arêtes les segments [PQ] reliant les cellules adjacentes V(P) et V(Q).
Propriété : Deux arêtes ne se coupent pas. Autrement dit, le maillage de Delaunay est un graphe.
Dans l'introduction, nous avons caractérisé le diagramme de Voronoi à l'aide des distances entre les points du plan et les sites. On peut faire de même pour le maillage de Delaunay, mais cette fois à partir des angles.
Propriété : Pour tout ensemble de points dans le plan, la triangulation de Delaunay maximise le minimum de tous les angles. C'est même l'unique triangulation optimale du point de vue angulaire.
Cette propriété fait d'un maillage de Delaunay l'une des méthodes les plus utilisées pour générer des maillages automatiques en éléments finis.
Cette propriété fait d'un maillage de Delaunay l'une des méthodes les plus utilisées pour générer des maillages automatiques en éléments finis.
Implémentation du maillage de Delaunay
Soit toujours notre ensemble de n points (Pi) avec 1≤i≤n . Les différentes étapes de construction sont les suivantes :
- On crée 3 points P-2 , P-1 et P0 qui englobent tous les points Pi (cf figure 1);
- on définit la triangulation T initiale comme le seul triangle P-2P-1P0 ;
- puis pour 1≤r≤n :
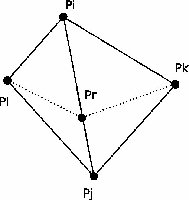
- on trouve le triangle PiPjPk qui contient le point Pr ;
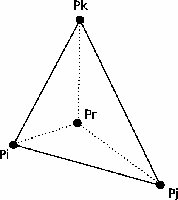
- soit Pr tombe à l'intérieur du triangle (cf figure 2) et donc :
- on divise le triangle PiPjPk en 3 triangles en reliant Pr aux trois sommets ;
- on légalise [PiPj] , [PjPk] et [PkPi] avec Pr (cf section suivante) ;
- soit Pr tombe sur une arête du triangle, disons [PiPj] (cf figure 3), et donc :
- on trouve l'autre point Pl ≠ Pk qui forme un autre triangle avec les points Pi et Pj ;
- on relie Pr à Pk et Pl . On a donc maintenant 4 triangles au lieu de 2 ;
- on légalise [PiPk] , [PkPj] , [PjPl] et [PlPi] avec Pr .
- on retire les points P-2, P-1 et P0 et leurs arêtes incidentes ;
- on retourne la triangulation T.
Fig 1 : Configuration initiale
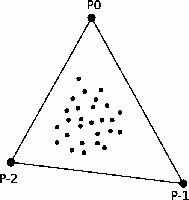

Fig 2: Pr tombe dans l'intérieur du triangle

Légalisation
Voyons maintenant ce que signifie le caractère légal d'une arête, et comment on le vérifie.
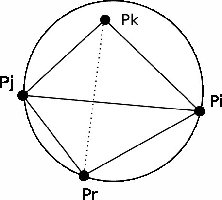
On se place dans le cas de l'insertion d'un point Pr dans le triangle P0PiPj . On suppose qu'il ne tombe pas sur une arête du triangle. On considère une arête de ce triangle ( disons [PiPj] ). Soit Pk le point tel que PiPjPk soit adjacent a P0PiPj .
L'arête est illégale si le point Pk est à l'intérieur du cercle circonscrit au triangle PrPiPj (cf figure 4). D'un point de vue angulaire, cela signifie que les angles (PiPjPk) et (PjPiPk) sont trop petits.
Si c'est le cas, on légalise alors de la manière suivante :
L'arête est illégale si le point Pk est à l'intérieur du cercle circonscrit au triangle PrPiPj (cf figure 4). D'un point de vue angulaire, cela signifie que les angles (PiPjPk) et (PjPiPk) sont trop petits.
Si c'est le cas, on légalise alors de la manière suivante :
- on supprime l'arête [PiPj] et on la remplace par l'arête [PrPk] ;
- on légalise [PiPk] et [PjPk] avec Pr .
A noter que cette transformation du maillage n'est que locale. D'un point de vue "extérieur", cela ne change rien.
Généralisation de la méthode à la sphère
Nous allons maintenant généraliser cette méthode à une sphère.
On considère donc toujours un ensemble de n points répartis cette fois-ci sur une sphère. L'algorithme de construction du maillage est identique à celui présenté auparavant (cf section implémentation). Néanmoins, l'étape consistant à trouver le triangle contenant le point à insérer ainsi que la légalisation sont légèrement plus compliquées. Nous allons donc les détailler
Trouver le bon triangle
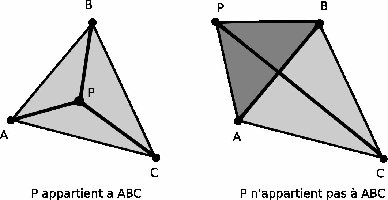
Lorsque le problème est plan, il est facile de déterminer si un point P appartient à un triangle ABC dont l'aire est notée A0. Pour cela, on trace les 3 triangles ABP, BCP, ACP, puis on calcule leurs aires respectives A1, A2, A3 (cf figure 5).
Le point P appartient à ABC si et seulement si :
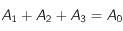
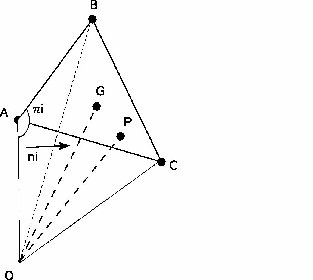
Dans le cas de la sphère, on aurait pu faire pareil en considérant le projeté du point P dans le plan du triangle. Néanmoins, nous allons utiliser une autre méthode plus facile à implémenter. Soit G le centre de gravité du triangle, et Π1, Π2, Π3, les plans contenant les triangles OAB, OBC et OAC.
Pour que P soit dans le triangle ABC, il faut que pour chacun de ces plans, P et G soient situés du même côté. En d'autres termes, il faut et il suffit que pour tout i=1,2,3 :
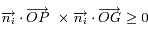
où ni est un vecteur normal à Πi .(cf figure 6).
Le point P appartient à ABC si et seulement si :
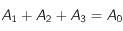
Dans le cas de la sphère, on aurait pu faire pareil en considérant le projeté du point P dans le plan du triangle. Néanmoins, nous allons utiliser une autre méthode plus facile à implémenter. Soit G le centre de gravité du triangle, et Π1, Π2, Π3, les plans contenant les triangles OAB, OBC et OAC.
Pour que P soit dans le triangle ABC, il faut que pour chacun de ces plans, P et G soient situés du même côté. En d'autres termes, il faut et il suffit que pour tout i=1,2,3 :
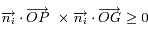
où ni est un vecteur normal à Πi .(cf figure 6).
Légalisation pour la sphère
On généralise donc le cas plan au cas sphérique en disant que l'arête [PiPj] est illégale si Pk est situé à l'intérieur de la calotte circonscrite au triangle PrPiPj (cf section précédente pour les notations).
L'algorithme de résolution est ensuite le même que dans le cas plan.
L'algorithme de résolution est ensuite le même que dans le cas plan.
Espacement minimal des sites
Les différents sites du maillage de Delauney correspondent à des points générés aléatoirement sur la sphère. Considérant le fait que ce maillage sphérique est développé dans l'optique de simulations de processus physiques, il est pertinent de vouloir limiter la distance minimale entre deux sites voisins. Le but est en effet de simuler la catalyse de la réaction 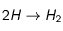 sur les grains de poussière dans le milieu interstellaire, chaque grain étant parsemé de sites réactionnels. Afin de pouvoir simuler ce phénomène physique et modéliser un grain, une possibilité consiste justement à utiliser ce maillage de Delauney sphérique, chaque site "géométrique" placé de manière aléatoire correspondant à un site réactionnel.
sur les grains de poussière dans le milieu interstellaire, chaque grain étant parsemé de sites réactionnels. Afin de pouvoir simuler ce phénomène physique et modéliser un grain, une possibilité consiste justement à utiliser ce maillage de Delauney sphérique, chaque site "géométrique" placé de manière aléatoire correspondant à un site réactionnel.
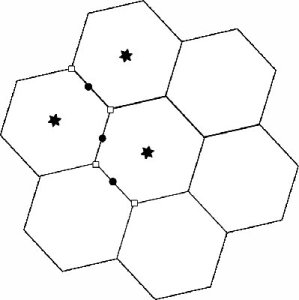
Toutefois des considérations physiques nous indiquent qu'il est raisonnable d'imposer une distance minimale entre deux sites voisins. Un exemple illustratif est celui d'un grain en graphite. La structure cristalline hexagonale d'un tel grain possède trois types de sites réactionnels capables de fixer un atome d'hydrogène. Une première catégorie de sites (représentée par des étoiles sur la figure) correspondant au centre des hexagones dans la maille cristalline, une seconde (représentée par des carrés sur la figure) correspondant aux noeuds de la maille (qui correspondent aux atomes de carbone) et une dernière (représentée par des points sur la figure) correspondant au centre des liaisons carbone-carbone.
Finalement le critère adopté pour la construction du maillage est une distance inter-site minimale égale à 0.3 fois la distance inter-site moyenne. Il est possible de discuter l'exactitude du facteur adopté, cependant 0.3 semble être une valeur pertinente.
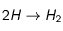 sur les grains de poussière dans le milieu interstellaire, chaque grain étant parsemé de sites réactionnels. Afin de pouvoir simuler ce phénomène physique et modéliser un grain, une possibilité consiste justement à utiliser ce maillage de Delauney sphérique, chaque site "géométrique" placé de manière aléatoire correspondant à un site réactionnel.
sur les grains de poussière dans le milieu interstellaire, chaque grain étant parsemé de sites réactionnels. Afin de pouvoir simuler ce phénomène physique et modéliser un grain, une possibilité consiste justement à utiliser ce maillage de Delauney sphérique, chaque site "géométrique" placé de manière aléatoire correspondant à un site réactionnel.Toutefois des considérations physiques nous indiquent qu'il est raisonnable d'imposer une distance minimale entre deux sites voisins. Un exemple illustratif est celui d'un grain en graphite. La structure cristalline hexagonale d'un tel grain possède trois types de sites réactionnels capables de fixer un atome d'hydrogène. Une première catégorie de sites (représentée par des étoiles sur la figure) correspondant au centre des hexagones dans la maille cristalline, une seconde (représentée par des carrés sur la figure) correspondant aux noeuds de la maille (qui correspondent aux atomes de carbone) et une dernière (représentée par des points sur la figure) correspondant au centre des liaisons carbone-carbone.
Finalement le critère adopté pour la construction du maillage est une distance inter-site minimale égale à 0.3 fois la distance inter-site moyenne. Il est possible de discuter l'exactitude du facteur adopté, cependant 0.3 semble être une valeur pertinente.
Sites réactionnels dans la maille d'un grain en graphite

Obtention des cellules de Voronoi à partir du maillage
Une fois le maillage de Delaunay construit, la prochaine étape consiste à tracer les cellules de Voronoi.
Soit P un site dont on souhaite tracer la cellule V(P). Soient {Vi} l'ensemble des voisins de P. On commence par classer les voisins. Pour cela, on définit 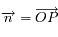 comme vecteur portant l'axe de rotation. Ensuite, on choisit un voisin de référence au hasard et on classe les voisins en "tournant" dans le sens trigonométrique autour de
comme vecteur portant l'axe de rotation. Ensuite, on choisit un voisin de référence au hasard et on classe les voisins en "tournant" dans le sens trigonométrique autour de 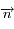 (cf figure 7).
On assimile ensuite la cellule à un "toit". Pour chaque couple successif de voisins
(cf figure 7).
On assimile ensuite la cellule à un "toit". Pour chaque couple successif de voisins 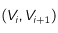 , on se place dans le plan
, on se place dans le plan 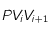 . On calcule les sommets
. On calcule les sommets 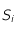 et
et 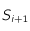 de la cellule comme décrit dans la section 1.
de la cellule comme décrit dans la section 1.
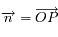 comme vecteur portant l'axe de rotation. Ensuite, on choisit un voisin de référence au hasard et on classe les voisins en "tournant" dans le sens trigonométrique autour de
comme vecteur portant l'axe de rotation. Ensuite, on choisit un voisin de référence au hasard et on classe les voisins en "tournant" dans le sens trigonométrique autour de 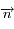 (cf figure 7).
On assimile ensuite la cellule à un "toit". Pour chaque couple successif de voisins
(cf figure 7).
On assimile ensuite la cellule à un "toit". Pour chaque couple successif de voisins 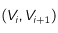 , on se place dans le plan
, on se place dans le plan 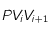 . On calcule les sommets
. On calcule les sommets 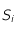 et
et 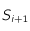 de la cellule comme décrit dans la section 1.
de la cellule comme décrit dans la section 1.
Calcul des probabilités d'arrivée
La probabilité d'arrivée d'une particule sur une cellule bien précise est proportionnelle à l'aire de cette dernière : plus la cellule est grande, plus la probabilité qu'une particule tombe dessus est forte.
Comme dit précédemment, on assimile donc la cellule à un toit dont le sommet sont notés 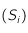 . On calcule l'aire approximativement en sommant l'aire de tous les triangles :
. On calcule l'aire approximativement en sommant l'aire de tous les triangles :
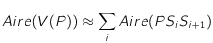
Pour finir, on normalise cette aire pour obtenir la probabilité d'arrivée :
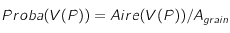
où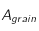 est l'aire totale du grain.
Cela constitue une bonne approximation lorsqu'on a un grand nombre de sites, même si rigoureusement on n'a pas
est l'aire totale du grain.
Cela constitue une bonne approximation lorsqu'on a un grand nombre de sites, même si rigoureusement on n'a pas 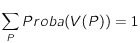 .
.
 . On calcule l'aire approximativement en sommant l'aire de tous les triangles :
. On calcule l'aire approximativement en sommant l'aire de tous les triangles :
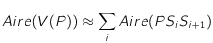
Pour finir, on normalise cette aire pour obtenir la probabilité d'arrivée :
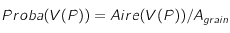
où
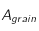 est l'aire totale du grain.
Cela constitue une bonne approximation lorsqu'on a un grand nombre de sites, même si rigoureusement on n'a pas
est l'aire totale du grain.
Cela constitue une bonne approximation lorsqu'on a un grand nombre de sites, même si rigoureusement on n'a pas 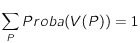 .
.