Réalisation de maillages pour une application aux automates cellulaires
Auteurs:
Sonny Lion, Alexis Petit
Date de création :
3 octobre 2012
Date de mise à jour :
12 décembre 2012
Table des matières
Liste des paramètres d'entrée de l'applet
- titre : Nombre de colonnes
label : ncolonnes
Nombre de colonnes de la grille. Dans le cas du maillage hexagonal le nombre de colonnes sera pair afin de gérer les conditions
périodiques.
- titre : Nombre de lignes
label : nlignes
Nombre de colonnes de la grille.
- titre : Nombre de points (Voronoi)
label : npoints
Nombre de points utilisés pour construire le maillage de type Delaunay-Voronoi
- titre : Grossissement
label : gamma
Grossissement
- titre : Choix de la grille
label : gtype
Sélectionne le type de grille (carrée, hexagonale ou Delaunay-Voronoi).
Valeurs possibles :
Grille carrée
Grille Hexagonale
Grille de Voronoi
- titre : Mode du test
label : mode
Sélectionne le test qu'on applique à notre grille
Valeurs possibles :
Grille initialisée au hasard
Point test libre
Point test fixe
- titre : rayon
label : rayon
Rayon de recherche des voisins
- titre : pointTestX
label : pointTestX
Coordonnée x du point test
- titre : pointTestY
label : pointTestY
Coordonnée y du point test
Liste des paramètres de sortie de l'applet
Champ
Modélisation de phénomènes émergents
Introduction
Le fonctionnement des automates cellulaires repose sur l'évolution d'une grille de cellules pouvant prendre plusieurs états
(la cas le plus simple étant une grille de cellules pouvant passer d'un état mort ou vivant, 0 ou 1, up ou down). L'ensemble
des états peut être grand mais la complexité augmente alors radicalement. L'état d'une cellule au temps t+dt est déterminé
par l'ensemble des états des cellules adjacentes au temps t, associé à une loi d'évolution. Ce principe donne lieu à tout
une famille d'applications que l'on appelle les automates cellulaires. Nous nous intéressons plus spécifiquement aux automates
cellulaire 2D. La mise en oeuvre et l'étude de différentes lois d'évolution en vue d'une application à des problèmes physiques
particuliers est réalisée par deux groupes : l'un s'intéresse à un modèle de
réaction-diffusion de Turing et l'autre à un
modèle d'Ising . Notre groupe, dont le travail est présenté sur cette page, a eu pour objectif la réalisation d'un maillage adapté à la
réalisation d'automates cellulaires. Nous avons développé plusieurs types de maillages présentant chacun des avantages et
des inconvéniants. L'intérêt de chacun sera discuté dans les sections qui suivent en se basant d'une part sur les avantages
théoriques mais sur notre impression lors du développement (difficulté rencontrées, complexité des algorithmes).
-
Objectifs
-
Le maillage d'une simulation numérique constitue la base sur lequel les processus physiques seront modélisés. Un maillage
est une discrétisation de l'espace et du temps afin de traiter numériquement par ordinateur un système continu. Dans notre
cas il permet de développer un modèle de système dynamique discret particulièrement pertinent quand on regarde l'évolution
d'un grand nombre d'entité discrètes comme les spins des atomes d'un cristal (modèle Ising) ou les cellules d'un organisme
(modèle de Turing).
Un maillage se définit par un réseau qui détermine l'emplacement des sites de chaque cellule, et par un pavage qui remplit
l'espace de sorte qu'il n'y ai aucun trou entre les cellules. Nous avons choisi de développer trois types de maillages décrits
par ordre de complexité dans les paragraphes qui suivent. Nous présentons leur structure, l'algorithme qui permet de les générer
ainsi que certains détails techniques qui pourront aider une personne désirant exploiter le code pour une nouvelle utilisation.
En dernier recours nous vous renvoyons à la javadoc en lien en bas de page.
Il existe encore d'autres types de maillages comme par exemple le maillage triangulaire (déconseillé pour les raisons théoriques
expliquées en dessous) ou le maillage avec un pavage récursif où un polygone peut lui même être divisé en un polygone de même
nature mais de taille inférieure. En appliquant un algorithme récursif cela permet d'explorer avec une plus grande résolution
certaines régions de l'espace. Faute de temps nous n'explorerons pas cette quatrième possibilité.
Explications
Fonctionnement d'un automate cellulaire
Afin de comprendre la logique qui nous a guidé dans le développement de nos maillages il est nécessaire de dire quelques mots
sur les automates cellulaires (pour plus de détails ou peut se reporter à la documentation des groupes associés). Comme il
l'a déjà été dit, l'évolution de chaque cellule repose sur l'état des cellules adjacentes. Nous avons donc choisi de développer
notre maillage de telle sorte qu'il contienne des entités de type cellule pouvant passer d'un état booléen "vrai" ou "faux"
selon ce que l'on définit comme étant les cellules voisines. Chaque cellule doit connaître quelles sont les cellules adjacentes.
Le type orienté objet du langage java est tout à fait adapté à cela.
Les trois options de maillage mettent en oeuvre toujours la même structure de code. D'une part une classe "grille" (grille_carree.java,
grille_hexa.java et grille_voronoi.java) qui génère notamment une liste de cellules, d'autre part une classe cellule.java
qui permet de créer des objets "cellule" avec des variables contenant l'état de la cellule, une liste des cellules voisines,
et bien sur le point sur la grille associé à cette cellule. Une fois cette structure mise en place vient la question de la
méthode afin de générer un réseau de cellules (c'est-à-dire le maillage) sur lequel évoluera le système d'automates cellulaires.
Enfin précisons que l'évolution de l'état des cellules peut-être très facilement géré par la méthode evolution_grille() située
dans la classe principale TestGrille.java que nous employons pour réaliser quelques tests.
Discussion théorique sur le choix du maillage
Le choix du maillage est fondamental. Nous discutons ici des enjeux théoriques de chaque maillage.
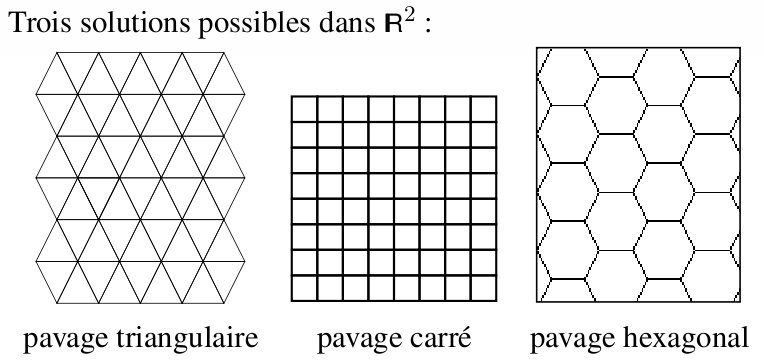
Il existe différents types de pavages réguliers dans le plan R2. On s'intéresse ici au pavage carré et hexagonal. Le pavage triangulaire présente peut d'intérêt pour la simulation de processus
physique.
Morphologie mathématique, Luc Brun (d’apres le cours de M. Coster)
- Isotropie : C'est en effet la structure du maillage qui détermine comment une particule va se déplacer. Le maillage sur une grille carrée
n'offre en effet que quatre possibilités de mouvement (bas, haut, gauche et droite) alors qu'un maillage hexagonal en offre
six. Il apparaît également qu'un maillage carré n'est pas isotrope. Si nous effectuons une rotation des vitesses de particules
se déplaçant sur le réseau nous remarquons que le système n'est pas invariant.Le système n'est invariant que pour des rotations
de 90°, 180°, 270° ou 360°. Une maille hexagonale offre davantage de symétries.
- Convexité : Un maillage discret induit forcément une perte de convexité ce qui pose problème dans la représentation d'une courbure. Par
exemple la réalisation d'un disque avec une grille carrée ou hexagonale ne peut se faire qu'avec un nombre élevé de cellules.
Sur la figure ci-dessous on voit que le maillage carré et le maillage hexagonal offre une représentation du disque différente.


A gauche : un disque à partir des huit premiers voisins de la cellule centrale réalisée sur une grille carrée. A droite :
idem mais avec une grille hexagonale.
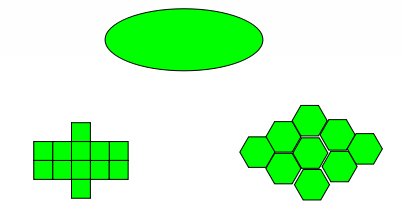
Il est par exemple difficile de représenter un ellipsoïde avec un maillage carré.
Morphologie mathématique, Luc Brun (d’apres le cours de M. Coster)
- Longueur de chemin : Selon le type de maillage la distance séparant un point à un autre n'est pas forcément la même. Plus précisément le plus
court chemin entre deux cellules peut être différent selon que la maille soit carrée ou hexagonale et souvent il n'est pas
unique. Sur les figures ci-dessous, nous avons un maillage carré et un maillage hexagonal. La distance euclidienne entre les
deux points x et y est la même dans les deux cas mais la longueur du chemin pour aller de x en y ne sera différente. De plus
le chemin le plus court n'est absolument pas unique.
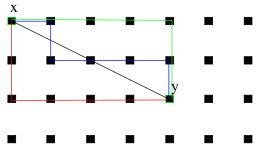
Réseau carré.
Morphologie mathématique, Luc Brun (d’apres le cours de M. Coster)
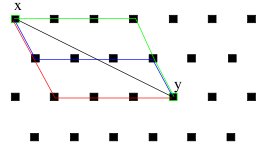
Réseau hexagonal.
Morphologie mathématique, Luc Brun (d’apres le cours de M. Coster)
- Choix des voisins : Encore une fois selon le type de maillage le choix des voisins ne se fera pas de la même façon. Dans le cas d'un pavage carré,
les quatres premiers voisins sont en contact par les arrêtes du carré tandis que si l'on considère les huit premiers voisins
la moitié sont en contact par un sommet. De plus si l'on considère la distance euclidienne de cette seconde moitié on s'apperçoit
qu'elle n'est pas la même que pour la première moitié. En revanche dans le cas d'un pavage hexagonal les premiers voisins
sont sans ambiguïté au nombre de six.
Le maillage avec un pavage triangulaire est tout à fait déconseillé en raison de la disposition des voisins. Une cellule triangulaire
possède douze voisins dont une moitié le touche par un côté et l'autre moitié par un sommet et avec une inclinaison de 120°.
Remarque :
Les maillages avec un pavage hexagonal sont souvent les mieux adaptés à la simulation de phénomènes physique notamment en
mécanique des fluides.
Maillage avec une grille carrée
Le maillage avec une grille carrée est la solution la plus facile à implémanter. Chaque site où se trouve une cellule est
réparti avec un pas δl=1 sur une surface rectangulaire ou carrée. L'algorithme permettant de créer le réseau de cellules et des plus simple :
- Pour tous les j de 0 au nombre de colonnes par pas de 1 et pour tous les i de 0 au nombre de lignes par pas de 1, créer une
cellule de coordonnée (i,j).
- Initialiser ensuite la cellule avec un état 1 ou 0.
Chaque site (c'est-à dire un noeud ou une cellule) est identifiée par des coordonnées (i,j) avec i et j des entiers. La recherche
des voisins en est facilité. Pour chaque cellule de coordonnées (i,j) on associe les quatre premiers voisins de coordonnées
(i+1,j), (i-1,j), (i,j+1), et (i,j-1). Si l'on recherche les huits premiers voisins alors on renvoit les cellules (i+1,j+1),
(i+1,j-1), (i-1,j+1), et (i-1,j-1) et ainsi de suite.
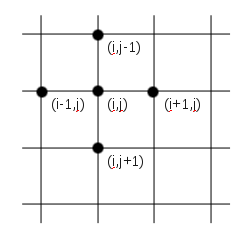
Position des sites de coordonnées (i,j) et des premiers voisins (i+1,j), (i-1,j), (i,j+1), et (i,j-1).
Une fois le réseau de cellules produit - dont chacune contient en mémoire la liste de ses voisins - on en déduit le pavage
c'est-à-dire la représentation spatiale des cellules. Enfin chaque cellule est représentée d'une couleur en fonction de son
état.

A chaque site du réseau (points en rouge) on associe une cellule et un pavage (carré en gris).
Le dernier point important concernant le maillage avec une grille carrée concerne la gestion des conditions périodiques. Le
bord supérieur est connecté avec le bord inférieur et le bord gauche est connecté avec le bord droit. La figure ci-dessous
on a un exemple de réalisation des conditions périodiques.

Voici une grille carrée avec une particule test étendue sur un rayon de 10 cellule dont le centre se trouve en haut à gauche.
Que ce soit pour le maillage carré ou la maillage hexagonal, la gestion de la périodicité se fait grâce à la méthode rechercheVoisins()
qui s'applique à l'objet de type grille. C'est elle qui attribue à chaque cellule ses plus proches voisins. En prenant soin
de prendre le cas des cellules aux bords et en leur déclarant comme voisins les cellules situées sur le bord opposé, l'applet
est ainsi capable de gérer facilement les conditions périodiques.
-
Exemple
-
Voici un exemple d'application de maillage avec une grille carrée. Chacune des cellules a été initialisée de façon aléatoire
avec un état 1 ou 0 qui se traduit par une couleur rouge ou bleu du pavage.
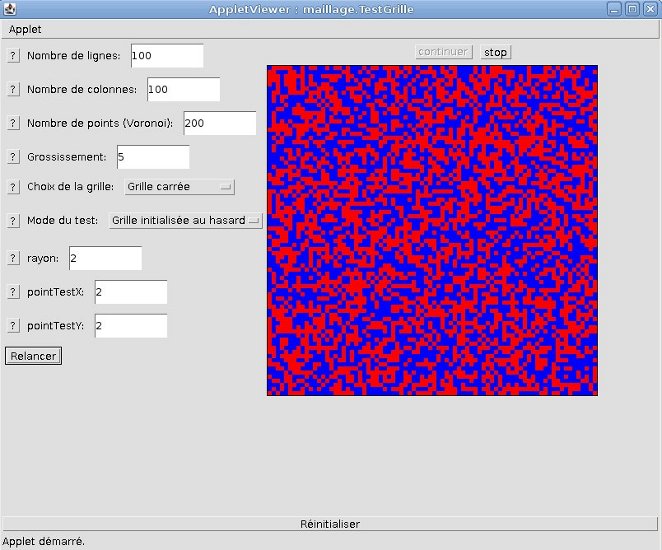
Capture écran de l'appliquette
Un autre exemple possible permettant de tester les conditions périodiques est la création d'un point test qui se baladerait
sur la grille avec une marche au hasard. On peut aussi créer une cellule test constituée de plusieurs voisins.
Remarque :
La grille carrée est très facile à implémenter. Elle constitue un bon premier test pour mettre en application les modèles
d'Ising ou de Turing. Les voisins se trouvent de façon immédiate car il suffit de reprendre la position d'une cellule et de
translater d'un pas δt. La rapidité d'exécution du code est donc avantageuse. Cependant pour les raisons évoquées à la section théorique, le maillage
carré n'offre pas un bon modèle physique. Particulièrement en ce qui concerne la recherche des premiers ou seconds voisins
qui n'est pas très correcte.
Maillage avec une grille hexagonale
Dans le cas du maillage hexagonale, nous avons choisit un algorithme légèrement plus complexe que celui du maillage carré
;
- On vérifie si le nombre de colonnes est impaire. Si c'est le cas il sera remplacé par l'entier paire inférieur le plus proche.
- Pour tous les points j de 0 au nombre de colonnes par pas de 1 et pour tous i de 0 au nombre de lignes par pas de 1, créer
une cellule de coordonnée :
- On initialise ensuite les cellules avec une valeur 0 ou 1.
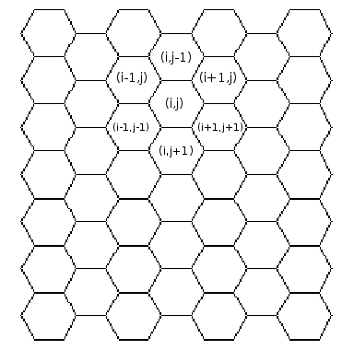
Disposition des cellules avec leur indexage.
Outre les arguments déjà avancés précédemment, le maillage avec une grille hexagonale facilite la détermination des premiers
voisins d'une cellule. En effet, une cellule donnée a toutes ses cellules adjacentes situées à égales distances.
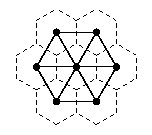
On voit que la distance qui sépare la cellule du milieu des cellules adjacente est la même pour toutes.
Tout comme pour la maillage carré nous avons réalisé le maillage hexagonal avec la topologie d'un tore. Notons que le nombre
pair de colonnes est imposé afin de gérer les conditions périodiques correctement.

Grille avec une particule test et ses dix premiers voisins activés.
-
Exemple
-
Voici un exemple d'application de maillage hexagonal. Chacune des cellules ont été initialisé de façon aléatoire avec un état
1 ou 0 qui se traduit par une couleur rouge ou bleu du pavage.
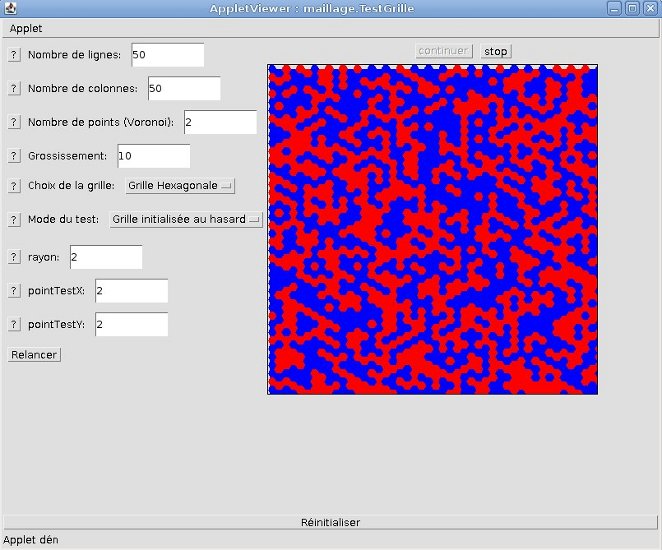
Capture d'écran de l'applet.
Maillage de type Delaunay-Voronoï
Remarque :
Face à la complexité de la construction d'un maillage de Delaunay-Voronoï, il nous a été impossible de parvenir à un programme
exploitable. Néanmoins la triangulation de Delaunay à partir d'une distribution aléatoire de points est opérationnelle. Elle
pourra être réutilisée dans un futur projet. Précisons également que les conditions périodiques n'ont pas été prise en compte
dans la triangulation de Delaunay.
On peut raisonnablement supposer que les maillages construits à partir d'un réseau périodique comme les grilles carrées ou
hexagonales sont bien adaptées pour modéliser des phénomènes comme le paramagnétisme dans les cristaux mais certains systèmes
sont plus réalistes s'ils sont représentés par une distribition aléatoire de points. Pour réaliser un tel maillage nous avons
choisi d'utiliser un algorithme de type Delaunay-Voronoi.
Le maillage de Delaunay-Voronoi s'obtient à partir d'une distribution aléatoire de point à laquelle nous avons tout de même
imposé une distance minimale entre chaque point. Nous allons décrire l'algorithme permettant de construire le maillage à partir
d'une telle distribution :
Algorithme de Delaunay :
- La première étape consiste à produire une liste de n points {P1, ..., Pn} circonscrite dans un triangle que l'on définit par
ses sommets P-1,P-2 et P-3.
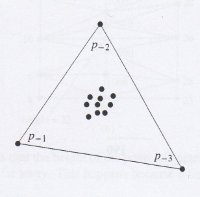
Triangle initial qui circonscrit la distribution de points.
Computational geometry
- Pour chaque point de la liste, nous effectuons une triangulation de Delaunay. On recherche à quel triangle appartient le point.
- Si le point est contenu dans un triangle :
- On relit ce point aux sommets du triangle ce qui nous amène à construire trois nouveaux triangles.
- On procède à la légalisation des arrêtes dans lequel se trouvait le point.
- Si le point tombe sur une arrête :
- On supprime cette arrête et on contruisons quatre nouveaux triangle en reliant le nouveau point aux sommets des deux triangles
initiaux.
- On procède à la légalisation des arrêtes des deux triangles auxquels appartenait l'arrête supprimée.
- On initialise chaque cellule avec une valeur 0 ou 1.
Détail du processus de légalisation :
Si nous n'effectuons pas le processus de légalisation nous avons bien une triangulation mais elle n'est pas de Delaunay. Le
processus de légalisation est donc au coeur de la construction du maillage de Delaunay. Les arrêtes de chaque nouveau triangle
doivent être vérifiées. Si l'une d'elle est déclarée illégale alors on procède un "flip", c'est-à-dire un changement de la
configuration des triangles. Prenons un exemple :
Si nous ajoutons un point Pr dans le triangle Δ1 (figure à gauche) alors nous devons créer trois nouveaux triangles en joignant ce point au sommet du triangle initial. Le
processus de légalisation va ensuite s'appliquer à chaque arrête du triangle.
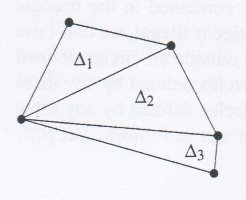
 Computational geometry
Computational geometry
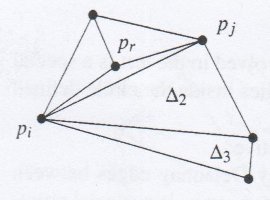
Regardons ce qui se passe dans le cas de la légalisation de l'arrête PiPj. Pour que l'arrrête soit déclarée légale, il faut que le cercle circonscrit par les trois points Pr, Pi et Pj ne contienne aucun autre point. Si c'est le cas comme le détail la figure ci-dessous alors l'arrête PiPj doit être supprimée et nous devons relier le point Pr à ce quatrième point Pk.
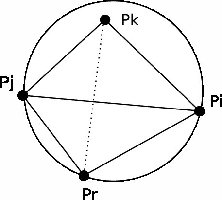 Computational geometry
Computational geometry
L'arrête du triangle Δ2 est donc supprimée et nous formons deux nouveaux triangles nommés ici Δ4 et Δ5. De plus l'algorithme de légalisation est récursif, c'est-à-dire que les arrêtes du nouveau triangle créé lors du processus
de légalisation doivent elles aussi être légalisées. C'est ainsi que l'arrête adjacente aux triangles Δ5 et Δ3 est supprimée pour construire les nouveaux triangles Δ6 et Δ7.
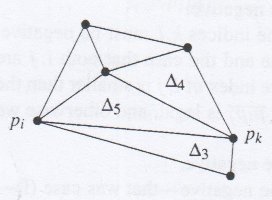
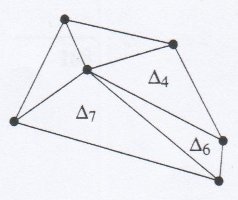 Computational geometry
Computational geometry
Si nous remplissons ces critères alors nous aurons bien une triangulation de Delaunay. Concrétement elle nous permet d'associer
chaque point à ses plus proche voisins. Enfin la dernière étape consiste à supprimer les points P-1, P-2 et P-3 du maillage.
Le diagramme de Voronoï
La diagramme de Voronoï est le dual de la triangulation de Delaunay. Pour obtenir les points constituant les cellules de Voronoï
il faut tracer les médiatrices aux segments joignant chaque cellule qui constituent le graphe de Delaunay. Les points de Voronoï
se trouvent à l'intersection des médiatrices.
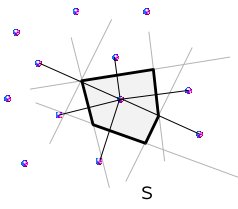
Frédéric Feyel - ONERA - DMSE/LCME
On obtient alors un pavage remplissant tout l'espace.
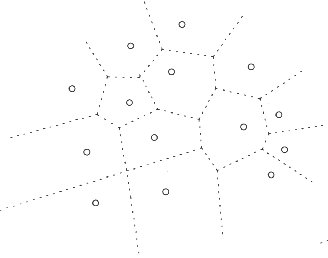
Frédéric Feyel - ONERA - DMSE/LCME
Remarque :
Un maillage de Delaunay-Voronoï peut-être difficile à gérer par un ordinateur aux ressources insuffisantes. Si le nombre de
points est trop important le processus de légalisation peut fortement augmenter le temps d'initialisation de l'applet.
-
Exemple
-
Voici un exemple d'application de la triangulation de Delaunay. Chaque carré représente un point distribué au hasard dans
une zone carrée. Les couleurs rouge et bleu correspondent à l'état de chaque cellule associée à un point. On a ici la génération
d'une triangulation de Delaunay avec une initialisation au hasard de 350 cellules disposées elle aussi au hasard dans un carré
de 50 lignes et 50 colonnes.
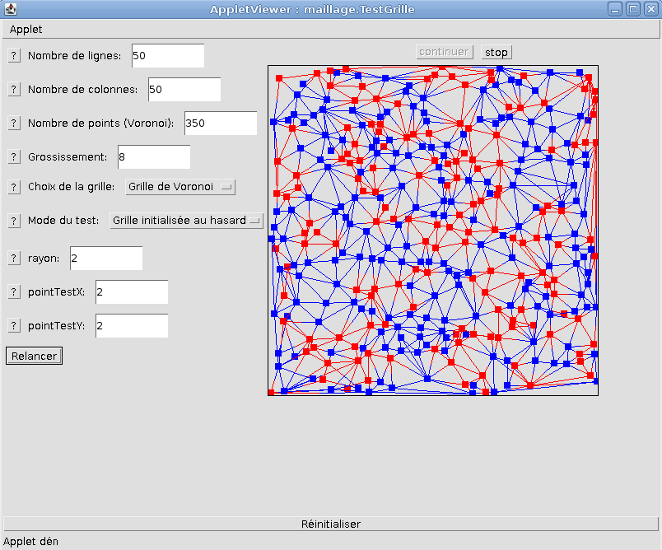
Capture d'écran de l'applet.
Mode d'emploi de l'applet
Nous avons créé une appliquette java afin de tester les différents maillages. Nous pouvons choisir si nous voulons un maillage
carré, hexagonal ou une triangulation de Delaunay à partir d'un nombre n de points. Un certains nombre de paramètre sont à
régler pour obtenir le maillage :
- La taille en donnant le nombre de lignes et de colonnes.
- Le grossissement pour visualiser l'ensemble du maillage s'il dépasse la frontière de l'appliquette.
- Le nombre de points utilisés pour la triangulation de Delaunay.
- Le type de test que l'on applique au maillage :
Celui-ci peut-être :
- La visualisation d'une initialisation aléatoire de chaque cellule.
- La visualisation d'une particule se déplaçant selon une marche au hasard, de cellule en cellule, à travers la grille.
- La visualisation d'une cellule dont on aurait donné les coordonnées avec la possibilité d'activer les cellules adjacentes
grâce à l'option rayon. Une valeur 1 donne les premiers voisins, une valeur 2 donne les seconds voisins et ainsi de suite.
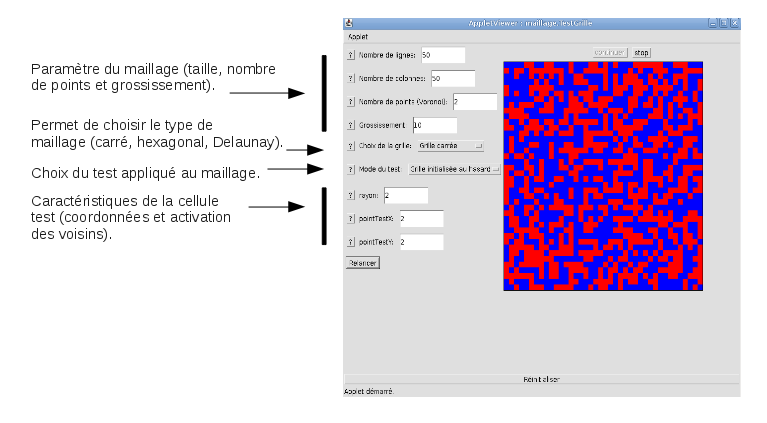
Capture d'écran de l'applet.
Pour plus d'informations on peut se référer à la javadoc.
Bibliographie
Et pour plus d'informations sur les maillages on peut se référer à deux livres :
- Ionut Danaila, Frédéric Hecht, Olivier Pironneau. Simulation numérique en C++, Dunod, Paris 2013.
- M. de Berg, M. van Krevel, M. Overmars, O. Schwarzkopf. Computational geometry . Springer Editions










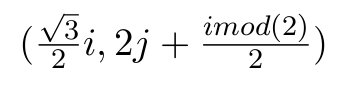






 Computational geometry
Computational geometry
 Computational geometry
Computational geometry

 Computational geometry
Computational geometry
 Frédéric Feyel - ONERA - DMSE/LCME
Frédéric Feyel - ONERA - DMSE/LCME
 Frédéric Feyel - ONERA - DMSE/LCME
Frédéric Feyel - ONERA - DMSE/LCME

