Refroidissement Laser
Auteur: Camille Charignon, Cédric Collet
Date de création :
06/10/2009
Date de mise à jour :
23/12/2009
Table des matières
Liste des paramètres d'entrée de l'applet
-
titre : Vitesse Initiale
label : v0
unités : m/s
Vitesse initiale de l'atome dans la direction x>0
-
titre : Durée du Ralentissement
label : deltat
unités : s
Durée de l'action des lasers
-
titre : Desaccord Laser-Résonnance
label : dw
unités : w0
Désaccord entre le laser et la résonnance:wL = w0 + dw*w0
-
titre : Atome Choisi
label : atome
Nom de l'atome refroidi
Valeurs possibles :
Liste des paramètres de sortie de l'applet
-
titre : temps
label : t
-
titre : vitesse(t)
label : vt
-
titre : position(t)
label : xt
-
titre : force(t)
label : ft
-
titre : vitesse
label : v
-
titre : force(v)
label : f
Introduction
Le refroidissement d'atomes par LASER est aujourd'hui couramment utilisé, notamment dans les horloges atomiques qui sont indispensables au bon fonctionnement du système GPS.
Il existe plusieurs types de refroidissement, mais nous nous limiterons ici au refroidissement par effet Doppler, qui permet néanmoins de ralentir les atomes jusqu'à une température de l'ordre de 0.1 mK.
-
Objectifs
-
Cette appliquette vous permet :
- De suivre l'évolution d'un seul atome
- De voir l'évolution d'un groupe d'atomes, ayant une certaine distribution de vitesse
Explications
Rappels de Mécanique Quantique
Introduction
La mécanique quantique est la théorie qui permet le mieux, aujourd'hui, de décrire le comportement microscopique de la matière et il est indispensable de la prendre en compte pour comprendre le refroidissement d'atomes par LASER. Nous n'entrerons cependant pas ici dans tous les détails : nous nous contenterons de faire appel aux notions pertinentes et nous les présenterons de la manière la plus pédagogique possible afin d'être accessible au plus grand nombre.
L'atome à deux niveaux
Dans la théorie de la mécanique quantique, les atomes ne peuvent pas avoir n'importe quelle énergie, mais sont nécessairement dans des "niveaux d'énergie" bien déterminés. On dit qu'ils sont quantifiés (d'où le nom de cette théorie d'ailleurs !).
Atome à deux niveaux
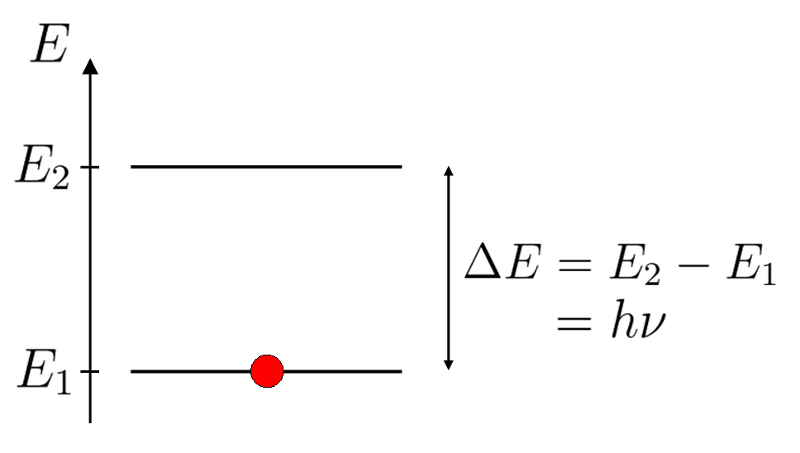
Schéma d'un atome à deux niveaux.
C. Charignon & C. Collet
Par conséquent, lorsqu'un atome interagit avec de la lumière, il ne peut pas le faire n'importe comment : il doit nécessairement absorber (ou réémettre) un photon d'une énergie correspondant à la différence d'énergie entre l'état initial et l'état final. C'est la constante de Planck
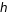
qui lie l'énergie
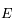
du photon et sa longueur d'onde
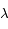
(ou sa fréquence
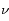
) selon :
Interaction Matière-Rayonnement
La matière a trois manières d'interagir avec le rayonnement auquel elle est soumise :
-
Absorption et exitation d'un atome
Un atome peut absorber un photon et ainsi monter sur un niveau d'énergie supérieure.
Absorption
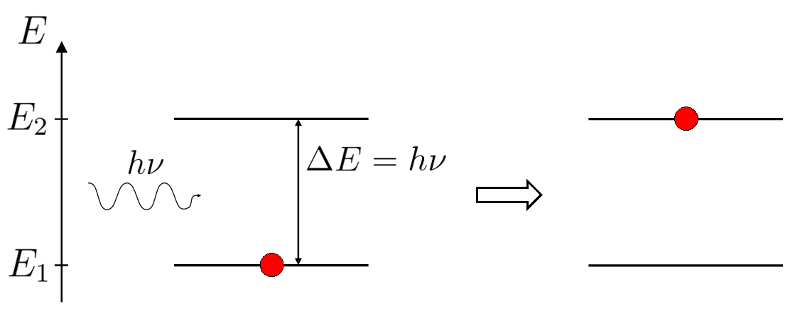
Schéma de l'excitation d'un atome par absorption d'un photon.
C. Charignon & C. Collet
Là aussi l'impulsion doit être conservée :
-
Emission spontanée
Lorsqu'un atome se trouve sur niveau excité, il cherche naturellement à retourner vers son niveau de plus basse énergie (qu'on appelle niveau fondamental). Pour cela, il émet un (ou plusieurs) photons afin de descendre de niveau en niveau, jusqu'à arriver sur le fondamental.
Entre deux niveaux, on peut attribuer une probabilité de désexcitation
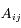
, qui est la mesure du nombre
moyen d'atomes qui passent du niveau

au niveau
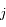
en une seconde.
Emission spontanée
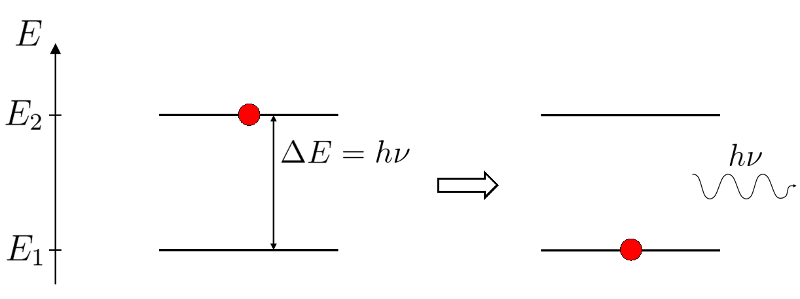
Schéma de la désexcitation spontanée d'un atome et émission d'un photon d'énergie 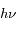 .
.
C. Charignon & C. Collet
Chaque photon émis de cette manière part dans une direction aléatoire et emporte une partie de l'impulsion de l'atome par la même occasion, de manière analogue au recul que subit le fusil lorsqu'on tire avec. L'impulsion d'un photon est définie comme :
où
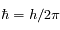
est la constante de Planck "réduite" et
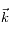
est le vecteur d'onde du photon émis.
L'impulsion étant une quantité conservée en physique, il faut que l'impulsion initiale de l'atome
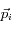
, son impulsion finale
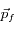
et l'impulsion du photon
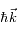
vérifient :
-
Emission induite
Emission induite d'un photon : Si l'atome se trouve sur un niveau excité et qu'il reçoit un photon, il peut émettre un deuxième photon, strictement identique au photon incident, et passer sur le niveau d'énergie inférieure. C'est d'ailleurs cette propriété qui est à la base du fonctionnement des LASER.
Emission induite
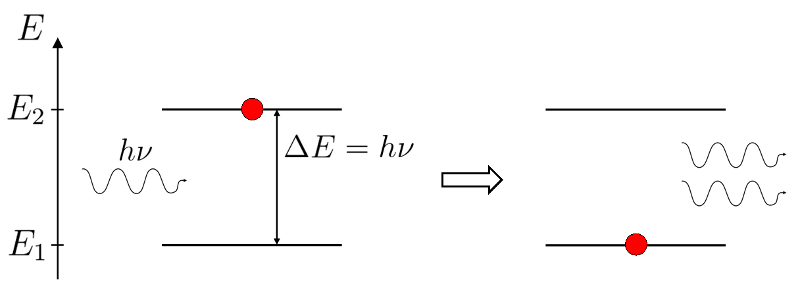
Schéma de l'émission induite d'un atome.
C. Charignon & C. Collet
La conservation de l'impulsion nous donne cette fois :
Remarque : Tous les vecteurs
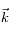
sont ici strictement identiques
Application : Interaction de l'atome de Rubidium avec un LASER
Le rayonnement d'un LASER est très particulier dans le sens où tous les photons qui le constitue sont identiques : ils ont notamment tous la même longueur d'onde. Cette propriété est très intéressante et va nous permettre d'exciter spécifiquement une transition. Or, nous l'avons vu précédemment, l'impulsion d'un atome varie lorsqu'il interagit avec le rayonnement.
Grandeurs liées au refroidissement Doppler
Tout d'abord, définissons quelques grandeurs utiles à partir de l'impulsion de recul
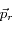
:
-
Vitesse de recul
-
Elle est définie à partir de la relation bien connue
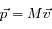
; où
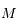
est la masse de la particule,
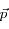
et
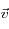
respectivement son impulsion et sa vitesse. On a donc :
-
Energie de recul
-
On la définit comme une énergie cinétique, à partir de la vitesse de recul
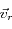
:
-
Température de recul
-
La
température de recul est quant à elle définie à partir de l'énergie de recul, en utilisant la constante de Boltzmann
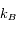
pour les lier :
Etape 1 : Absorption d'un photon du rayonnement LASER
Partons d'un atome sur le niveau fondamental et ayant une impulsion
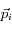
. Il absorbe un photon et passe donc sur un niveau excité en "gagnant" une impulsion
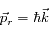
. Si
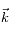
et
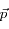
ont des sens différents, l'atome est freiné.
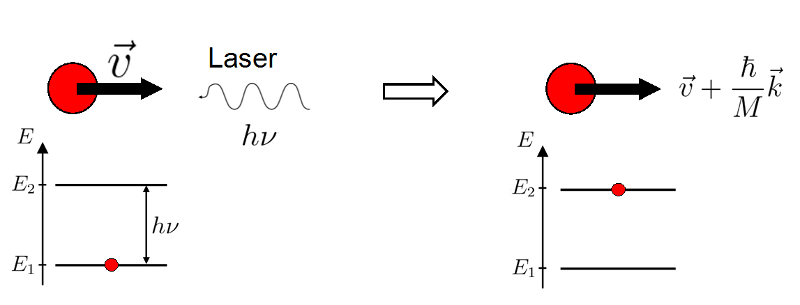
Schéma de la première étape du ralentissement Doppler de l'atome de Rubidium : absorption d'un photon du rayonnement LASER et ralentissement de l'atome d'une quantité de mouvement 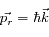 .
.
C. Charignon & C. Collet
Ensuite, une fois sur le niveau 2, l'atome a deux manières possibles de se désexciter : par émission induite (il est en effet soumis continument au rayonnement LASER) ou bien par émission spontanée.
Les conséquences de chacune de ces possibilités sont explorées dans les deux parties suivantes.
Première étape 2 possible : désexcitation par émission induite
L'atome excité peut recevoir un nouveau photon et alors se désexciter par émission induite. Le photon qu'il émet alors est, par définition, identique au photon incident. Et, comme nous sommes en présence d'un rayonnement LASER, le photon incident (ayant provoqué l'émission induite) et le tout premier photon (ayant excité l'atome) sont également identiques.
Le photon émis annule donc tout ce qu'avait provoqué le photon absorbé, puisque l'atome gagne une impulsion
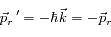
. Ainsi :
Deuxième étape du cycle "Absorption - Emission induite"
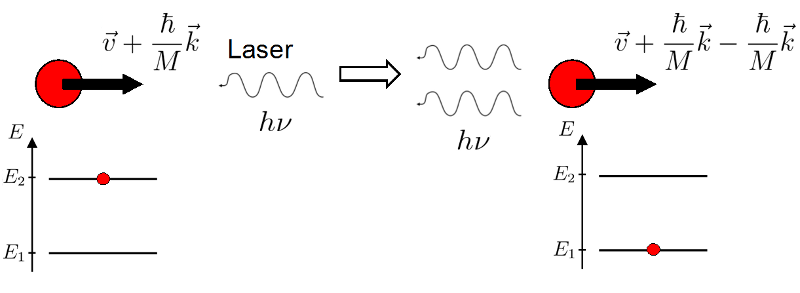
Schéma de l'interaction de l'atome de Rubidium excité avec le faisceau LASER lors d'une émission induite.
C. Charignon & C. Collet
Seconde étape 2 possible : désexcitation par émission spontanée
L'atome peut aussi se désexciter par émission spontanée pour retourner sur le niveau 1. Le photon alors émis part dans une direction aléatoire avec une impulsion
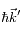
. La variation d'impulsion
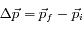
de l'atome est donc non nulle au final car le vecteur d'onde
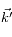
du deuxième photon est complètement indépendant de
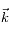
, celui du premier :
Deuxième étape du cycle "Absorption - Emission spontanée"
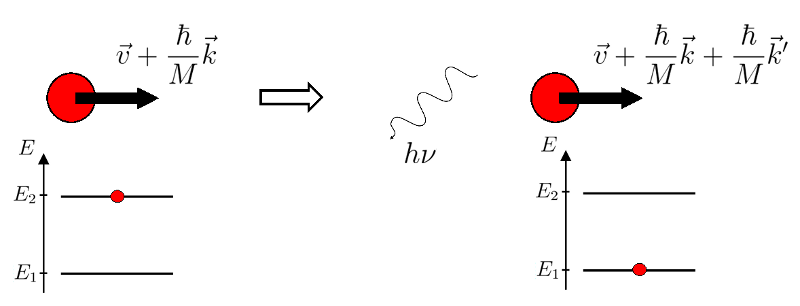
Schéma de l'interaction de l'atome excité de Rubidium avec le faisceau LASER lors d'une émission spontanée.
C. Charignon & C. Collet
Effet moyen du rayonnement LASER sur un atome
Résumons les effets des deux cycles d'interaction possibles sur la vitesse de l'atome :
Voyons maintenant l'effet du rayonnement LASER sur un nombre
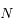
de cycles "Absorption puis Emission spontanée" (avec
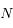
grand devant 1). A chacun de ces cycles, le photon qui excite l'atome est toujours le même car il provient du rayonnement LASER. L'atome gagne donc une vitesse
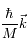
à chaque début de cycle et une vitesse
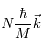
au bout de
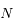
cycles .
Par contre, le photon émis spontanément par l'atome pour retourner sur son niveau fondamental a un vecteur d'onde
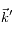
qui a une direction aléatoire. Lorsqu'on en somme un grand nombre, on obtient donc une contribution nulle :
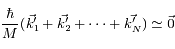
(où
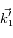
est le vecteur d'onde du premier photon émis spontanément,
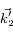
celui du deuxième, ... et
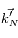
celui du dernier.)
Sur
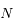
cycles "Absorption puis Emission spontanée", on voit que l'atome verra sa vitesse varier d'une quantité
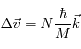
. Il suffit donc d'orienter le LASER de manière à avoir la vitesse
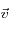
de l'atome et les vecteurs d'onde
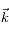
des photons "excitateurs" de sens opposés pour effectivement ralentir (et donc refroidir) l'atome.
Refroidissement et effet Doppler
Maintenant que nous avons vu qu'un rayonnement LASER bien choisi peut ralentir un atome, voyons comment on le met effectivement en oeuvre.
L'effet Doppler
Cet effet physique est bien connu : c'est lui qui "change" la hauteur de la sirène des véhicules d'urgence nous dépassant. La fréquence d'émission du son de la sirène ne change bien sur pas, c'est le fait que le véhicule se déplace par rapport à nous qui nous fait entendre la sirène plus aigue lorsqu'il s'approche et plus grave lorsqu'il s'éloigne.
La fréquence
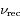
perçue par l'observateur est reliée à celle émise
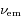
selon la relation (à condition que la vitesse relative
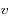
entre l'émetteur et le récepteur reste faible devant la vitesse de la lumière
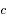
) :
-
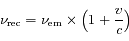 si la source se rapproche de l'observateur.
si la source se rapproche de l'observateur.
-
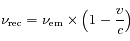 si la source s'éloigne de l'observateur.
si la source s'éloigne de l'observateur.
Or, comme il l'a été précisé au début, l'atome ne peut interagir qu'avec des photons ayant une énergie
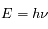
dans son référentiel. A cause de l'effet Doppler, l'atome risque donc de ne plus pouvoir absorber de photons dès qu'il n'aura plus la "bonne" vitesse, celle qui lui permet de voir des photons à la fréquence
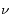
.
Cependant, la structure de l'atome est légèrement plus complexe que celle que nous avons présenté jusqu'ici : du fait de la durée de vie finie
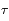
du niveau excité, il a aussi une certaine extension en énergie
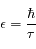
. Une image plus réaliste de la structure d'un atome à deux niveaux est donc la suivante :
Atome à deux niveaux plus réaliste
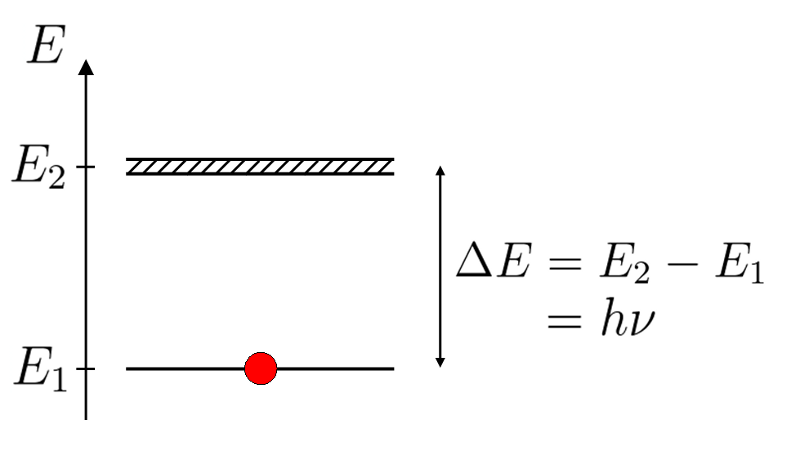
Schéma plus réaliste de l'atome à deux niveaux, prenant en compte la durée de vie finie du niveau excité.
C. Charignon & C. Collet
L'atome peut donc absorber des photons dont la fréquence n'est pas trop éloignée de sa fréquence propre
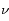
. Néanmoins, pour obtenir un refroidissement de l'atome aussi rapide que possible, il est nécessaire d'utiliser soit un LASER accordable, dont la fréquence varie pour s'accorder à la vitesse de l'atome ; soit l'effet Zeeman, qui modifie les niveaux d'énergie de l'atome grace à un champ magnétique. C'est cette dernière option qui est généralement choisie dans les horloges atomiques.
Ralentissement de l'atome
Nous allons donc supposer que l'atome a une probabilité non-nulle d'absorber un photon du faisceau LASER , mais que celle-ci décroit fortement dès qu'on s'éloigne un peu de sa fréquence propre.
Ensuite, il est nécessaire d'avoir deux faisceaux LASER légèrement désaccordés par rapport à la fréquence propre de l'atome et ayant des directions opposées l'une à l'autre. Ainsi, l'atome absorbera préférentiellement les photons du rayonnement LASER lorsqu'il aura la vitesse qui lui les fera voir à sa fréquence de résonance et on obtient l'efficacité maximale du ralentissement LASER lorsque celui-ci a une vitesse non-nulle.
Le deuxième faisceau LASER est nécessaire afin d'éviter que les atomes ne fassent demi-tour à force d'absorber des photons venant toujours de la même direction. La figure ci-dessous illustre le montage, en supposant que l'atome ne peut se déplacer que selon un axe horizontal.
Ralentissement d'un atome
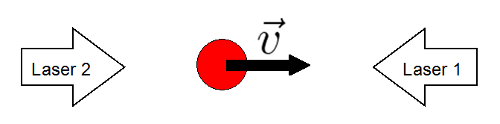
Pour être piégé, l'atome est soumis à six rayonnements LASER qui le confinent dans une certaine région de l'espace. Ici nous nous considérons que l'atome ne peut se déplacer que selon une direction, deux faisceaux suffisent donc.
C. Charignon & C. Collet
La mécanique quantique nous donne l'expression de la force qu'exerce un rayonnement LASER sur un atome : il s'agit d'une lorentzienne, centrée sur la vitesse de l'atome qui lui fait voir le rayonnement à sa fréquence propre. Voici son expression :
Avec :
-
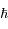 : la constante de Planck réduite.
: la constante de Planck réduite.
-
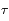 : la durée de vie du niveau excité.
: la durée de vie du niveau excité.
-
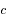 : la vitesse de la lumière.
: la vitesse de la lumière.
-
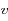 : la vitesse de l'atome.
: la vitesse de l'atome.
-
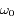 : la fréquence de la transition entre le niveau fondamental et le niveau excité.
: la fréquence de la transition entre le niveau fondamental et le niveau excité.
-
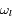 : la fréquence des photons émis par les deux faisceaux LASER.
: la fréquence des photons émis par les deux faisceaux LASER.
La force totale que subit l'atome est donc la somme de deux lorentziennes, une pour chaque LASER, dont l'allure est donnée ci-dessous.
Force moyenne
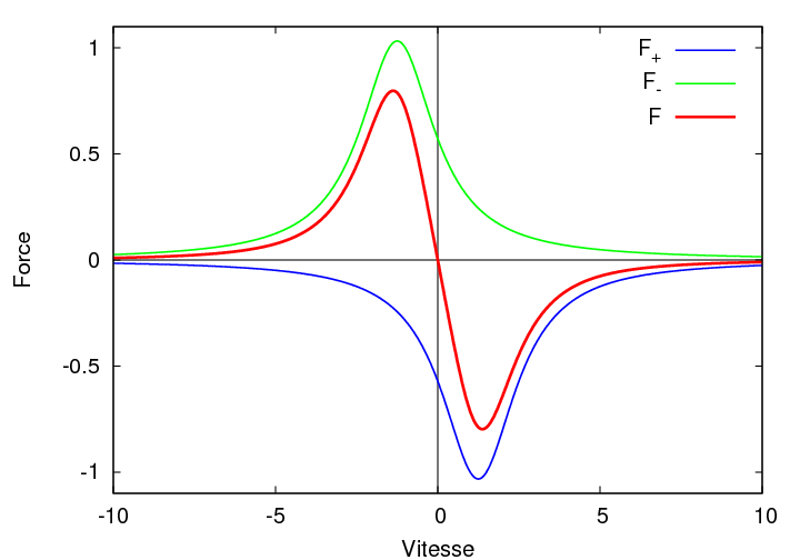
Allure de la force exercée par deux faisceaux LASER sur un atome de Rubidium (en rouge). Elle correspond à la somme de la force exercée par le faisceau LASER 1 (en bleu) et par le faisceau LASER 2 (en vert).
C. Charignon & C. Collet
C'est cette force que notre applet modélise et il vous possible de vérifier qu'il y a bien une vitesse pour laquelle la force est bien plus importante que pour les autres.
Exemple d'application du refroidissement d'atomes : l'horloge atomique
Mode d'emploi de l'applet
Appliquette AtomeUnique
Paramètres d'entré
Pour cette appliquette, trois ensembles prédéfinis permettent d'illustrer rapidement les points importants du problèmes. De plus quatres paramètres clefs du problèmes peuvent être réglés librement pour permettre une compréhension approfondie du problème pour les personnes plus intéréssées. La figure ci-dessous, montre les valeures des différents paramètres pour l'ensemble ForceMaximale.
Les trois ensembles de paramètres sont:
- L'ensemble ForceMaximale se place dans des conditions où l'atome subira une force maximale dès le début
- L'ensemble RalentissementMax correspond à un ralentissement maximum
- L'ensemble Accélération illustre le fait qu'un désaccord positif transforme le ralentissement en accélération
Les quatres paramètres sont:
- La vitesse initial de l'atome
- La durée du ralentissement
- Le désaccord entre la pulsation du laser et la pulsation de la transition atomique
- Le type d'atome refroidi (en fait uniquement du rubidium...)
Sélection des paramètres
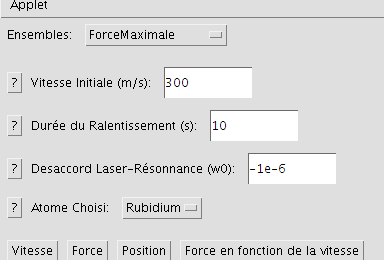
Écran s'affichant au lancement de l'appliquette
Affichages possibles
Il y a 4 affichages possibles:
-
Vitesse: Affiche la vitesse de l'atome en fonction du temps sur la durée choisie et pour les paramètres donnés
-
Force: Donne la force ressentie par l'atome pendant la durée de ralentissement
-
Position: Affiche la position de l'atome pendant l'expérience
-
Force en fonction de la vitesse: Montre le profil de la force correspondant au désaccord donné (accélération ou ralentissement selon le signe)
Exemple d'utilisation
Nous illusterons ici le fonctionnement de cette appliquette à travers les trois ensembles de paramètres prédéfinis, qui couvrent les apects intéréssants du problème.
Ensemble de paramètres "ForceMaximale" :
Pour cet ensemble de paramètres, on s'est placé à un désaccord correspondant à une force maximale pour la vitesse initiale. Sur les illustrations ci-dessous, on voit que le ralentissement est maximum au début puis à mesure que la vitesse diminue, la force diminue. En effet comme le montre le deuxième graphique, la force est piqué sur 300 m/s et dès qu'on s'en éloigne elle chute rapidement. C'est ce qui explique que le ralentissement ne soit pas si efficace que ça.
.
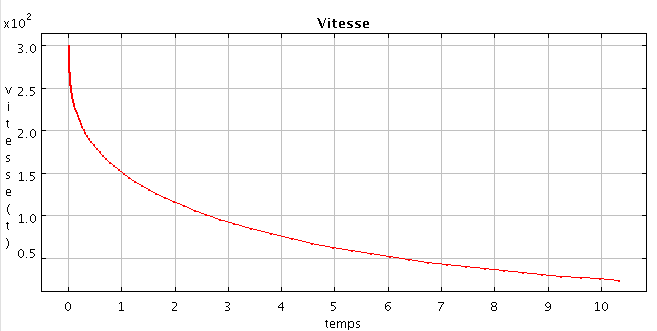
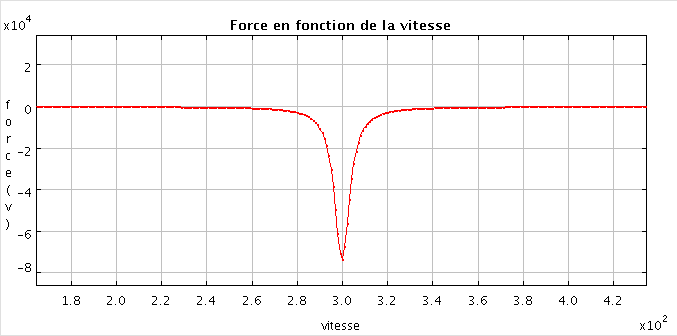
Vitesse et force pour les paramètres de "Forcemaximale"
Ensemble de paramètres "RalentissementMax" :
Cet ensemble de valeures, vise à montrer qu'on peut être un peu plus efficace si on part d'une vitesse légèrement plus grande que le maximum d'efficacité de la force. En effet de cette façon, l'atome passera plus de temps dans la zone piqué de la force. Cependant, comme dans le cas précédent, le ralentissement n'est efficace que pendant un temps relativement court.
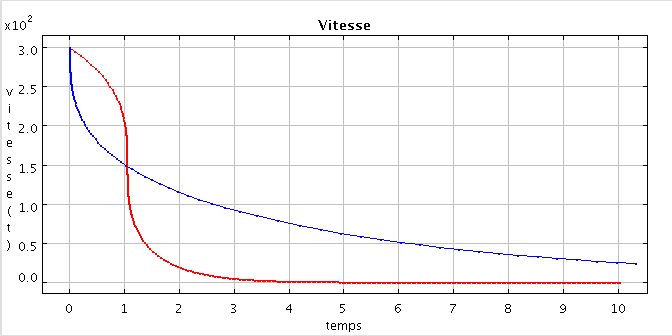
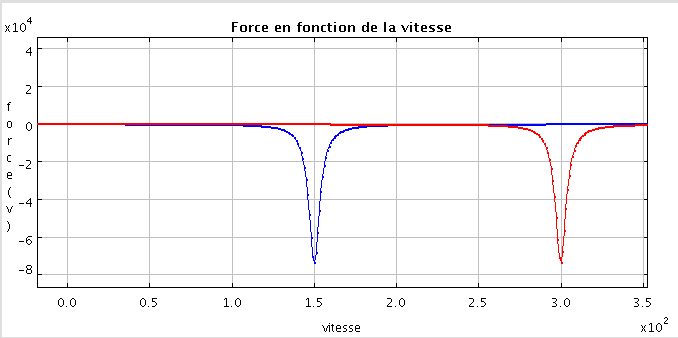
Vitesse et force superposées pour les paramètres de "Forcemaximale" et de "RalentissementMax", respectivement en bleu et rouge
Sur les figures ci-dessus, on a superposé la vitesse et la force dans le cas des deux ensembles ForceMaximale (courbe bleue) et RalentissementMax (courbe rouge). Il est évident que le ralentissement correspondant à la courbe rouge est beaucoup plus efficace. Dans ce cas la force maximale ne survient pas immédiatement et l'atome peut en subir les effets plus longtemp. La deuxième figure montre que l'on a déplacé le pic de ralentissement, qui se situe maintenant à 150 m/s. Ainsi en déplaçant ce pic, grâce au paramètre de désaccord entre la pulsation laser et la pulsation de la transition de l'Atome, on peut jouer sur l'instant t auquel survient le ralentissement. Nous laissons l'utilisateur essayer de trouver un ralentissement plus efficace... Bien sur dans la réalité l'astuce consiste à déplacer le pic de la force pour qu'il corresponde toujour à la vitesse de l'atome. De cette façon le ralentissement peut être très efficace. Mais cela demande aussi un ingrédient de plus... un champ magnétique !!
Ensemble de paramètres "Accélération" :
Pour ces valeurs, on a mis en évidence que le ralentissement recherché peut se transformé en accélération en changeant simplement le désaccord des pulsations. Sur les figures ci-dessous, on a tracé en bleu le ralentissement pour l'ensemble ForceMaximale et en rouge ce qu'il se passe pour un désaccord de signe opposé. Ainsi on voit que la force est de même amplitude mais de signe opposé, ce qui se traduit par une accélération pour l'Atome.
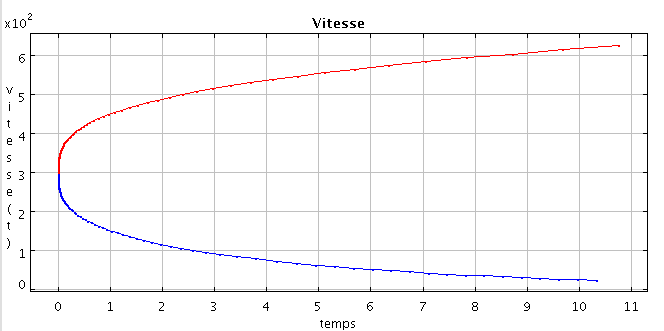
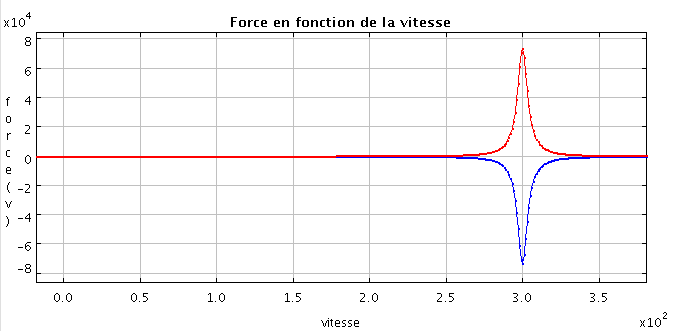
Vitesse et force superposées pour les paramètres de "Forcemaximale" et "Accélération", respêctivement en bleu et rouge
Les autres affichages: Force et Position :
Nous avons illustré abondament les sorties "Vitesse" et "Force en fonction du temps" car ce sont celles qui permettent de comprendre le phénomène. Mais l'affichage de la force en fonction du temps (grâce à "Force") peut être un parallèle intéressant pour aider à comprendre quand et pourquoi le ralentissement est maximum à un l'instant t. Ensuite, expérimentalement, quand on essaie de ralentir un atome il faut que celui ci reste confiné d'une manière où d'une autre dans un espace raisonnablement petit. C'est l'intéret de l'affichage "Position" qui montre (voir ci-dessous) que malheureusement notre atome n'est pas du tout confiné ! Il faudrait donc imaginer autre chose, par exemple un piège magnétique... ou alors trouver un laboratoire de 350m de long. Mais si on veut en faire une horloge atomique il faut absolument faire mieux, car une horloge de plusieures centaines de mètres serait trop encombrante!
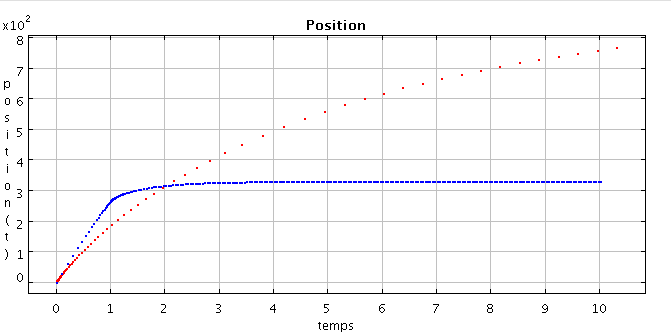
Position de l'atome en fonction du temps. En rouge pour les paramètres ForceMaximale en bleue pour RalentissementMax
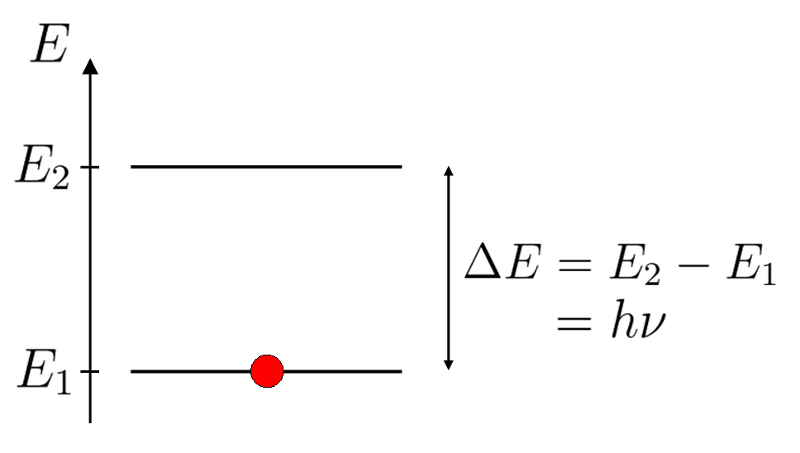
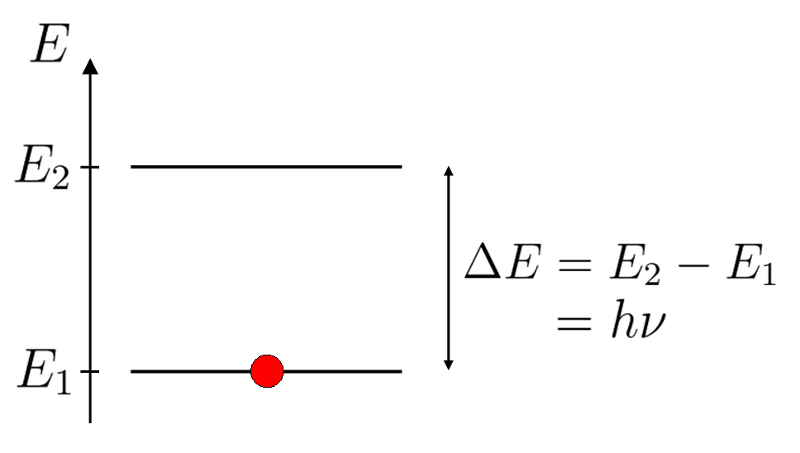
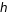 qui lie l'énergie
qui lie l'énergie 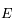 du photon et sa longueur d'onde
du photon et sa longueur d'onde 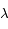 (ou sa fréquence
(ou sa fréquence 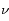 ) selon :
) selon :
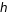 qui lie l'énergie
qui lie l'énergie 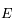 du photon et sa longueur d'onde
du photon et sa longueur d'onde 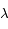 (ou sa fréquence
(ou sa fréquence 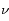 ) selon :
) selon :
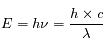

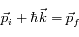
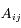 , qui est la mesure du nombre moyen d'atomes qui passent du niveau
, qui est la mesure du nombre moyen d'atomes qui passent du niveau  au niveau
au niveau 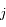 en une seconde.
en une seconde.

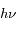 .
.
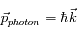
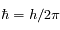 est la constante de Planck "réduite" et
est la constante de Planck "réduite" et 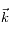 est le vecteur d'onde du photon émis.
est le vecteur d'onde du photon émis.
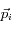 , son impulsion finale
, son impulsion finale 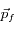 et l'impulsion du photon
et l'impulsion du photon 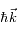 vérifient :
vérifient :
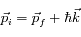

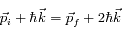
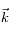 sont ici strictement identiques
sont ici strictement identiques
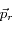 :
:
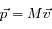 ; où
; où 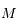 est la masse de la particule,
est la masse de la particule, 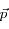 et
et 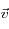 respectivement son impulsion et sa vitesse. On a donc :
respectivement son impulsion et sa vitesse. On a donc :
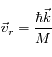
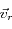 :
:
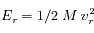
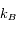 pour les lier :
pour les lier :
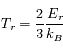
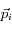 . Il absorbe un photon et passe donc sur un niveau excité en "gagnant" une impulsion
. Il absorbe un photon et passe donc sur un niveau excité en "gagnant" une impulsion 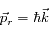 . Si
. Si 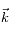 et
et 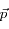 ont des sens différents, l'atome est freiné.
ont des sens différents, l'atome est freiné.

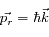 .
.
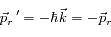 . Ainsi :
. Ainsi :
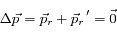

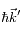 . La variation d'impulsion
. La variation d'impulsion 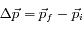 de l'atome est donc non nulle au final car le vecteur d'onde
de l'atome est donc non nulle au final car le vecteur d'onde 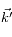 du deuxième photon est complètement indépendant de
du deuxième photon est complètement indépendant de 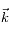 , celui du premier :
, celui du premier :
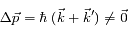

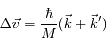 .
.
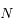 de cycles "Absorption puis Emission spontanée" (avec
de cycles "Absorption puis Emission spontanée" (avec 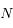 grand devant 1). A chacun de ces cycles, le photon qui excite l'atome est toujours le même car il provient du rayonnement LASER. L'atome gagne donc une vitesse
grand devant 1). A chacun de ces cycles, le photon qui excite l'atome est toujours le même car il provient du rayonnement LASER. L'atome gagne donc une vitesse 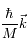 à chaque début de cycle et une vitesse
à chaque début de cycle et une vitesse 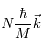 au bout de
au bout de 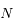 cycles .
cycles .
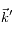 qui a une direction aléatoire. Lorsqu'on en somme un grand nombre, on obtient donc une contribution nulle :
qui a une direction aléatoire. Lorsqu'on en somme un grand nombre, on obtient donc une contribution nulle :
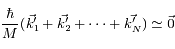 (où
(où 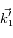 est le vecteur d'onde du premier photon émis spontanément,
est le vecteur d'onde du premier photon émis spontanément, 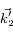 celui du deuxième, ... et
celui du deuxième, ... et 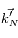 celui du dernier.)
celui du dernier.)
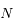 cycles "Absorption puis Emission spontanée", on voit que l'atome verra sa vitesse varier d'une quantité
cycles "Absorption puis Emission spontanée", on voit que l'atome verra sa vitesse varier d'une quantité 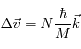 . Il suffit donc d'orienter le LASER de manière à avoir la vitesse
. Il suffit donc d'orienter le LASER de manière à avoir la vitesse 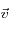 de l'atome et les vecteurs d'onde
de l'atome et les vecteurs d'onde 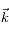 des photons "excitateurs" de sens opposés pour effectivement ralentir (et donc refroidir) l'atome.
des photons "excitateurs" de sens opposés pour effectivement ralentir (et donc refroidir) l'atome.
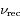 perçue par l'observateur est reliée à celle émise
perçue par l'observateur est reliée à celle émise 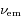 selon la relation (à condition que la vitesse relative
selon la relation (à condition que la vitesse relative 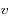 entre l'émetteur et le récepteur reste faible devant la vitesse de la lumière
entre l'émetteur et le récepteur reste faible devant la vitesse de la lumière 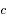 ) :
) :
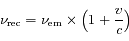 si la source se rapproche de l'observateur.
si la source se rapproche de l'observateur.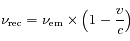 si la source s'éloigne de l'observateur.
si la source s'éloigne de l'observateur.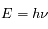 dans son référentiel. A cause de l'effet Doppler, l'atome risque donc de ne plus pouvoir absorber de photons dès qu'il n'aura plus la "bonne" vitesse, celle qui lui permet de voir des photons à la fréquence
dans son référentiel. A cause de l'effet Doppler, l'atome risque donc de ne plus pouvoir absorber de photons dès qu'il n'aura plus la "bonne" vitesse, celle qui lui permet de voir des photons à la fréquence 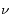 .
.
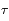 du niveau excité, il a aussi une certaine extension en énergie
du niveau excité, il a aussi une certaine extension en énergie 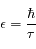 . Une image plus réaliste de la structure d'un atome à deux niveaux est donc la suivante :
. Une image plus réaliste de la structure d'un atome à deux niveaux est donc la suivante :

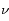 . Néanmoins, pour obtenir un refroidissement de l'atome aussi rapide que possible, il est nécessaire d'utiliser soit un LASER accordable, dont la fréquence varie pour s'accorder à la vitesse de l'atome ; soit l'effet Zeeman, qui modifie les niveaux d'énergie de l'atome grace à un champ magnétique. C'est cette dernière option qui est généralement choisie dans les horloges atomiques.
. Néanmoins, pour obtenir un refroidissement de l'atome aussi rapide que possible, il est nécessaire d'utiliser soit un LASER accordable, dont la fréquence varie pour s'accorder à la vitesse de l'atome ; soit l'effet Zeeman, qui modifie les niveaux d'énergie de l'atome grace à un champ magnétique. C'est cette dernière option qui est généralement choisie dans les horloges atomiques.

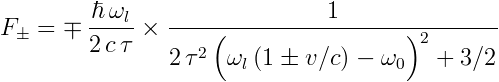
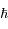 : la constante de Planck réduite.
: la constante de Planck réduite.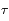 : la durée de vie du niveau excité.
: la durée de vie du niveau excité.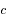 : la vitesse de la lumière.
: la vitesse de la lumière.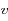 : la vitesse de l'atome.
: la vitesse de l'atome.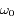 : la fréquence de la transition entre le niveau fondamental et le niveau excité.
: la fréquence de la transition entre le niveau fondamental et le niveau excité.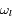 : la fréquence des photons émis par les deux faisceaux LASER.
: la fréquence des photons émis par les deux faisceaux LASER.







