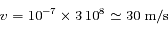Refroidissement Laser
Auteur: Camille Charignon, Cédric Collet
Date de création :
06/10/2009
Date de mise à jour :
23/12/2009
Table des matières
Liste des paramètres d'entrée de l'applet
-
titre : Nombre d'atomes
label : Natomes
Nombre d'atomes dans la population
-
titre : Vitesse initiale moyenne
label : v0
unités : m/s
Vitesse initiale moyenne de la population d'atomes
-
titre : écart-type de la distribution des vitesses
label : sigma
unités : m/s
L'écart-type de la distribution de vitesse des atomes dans l'hypothèse d'une distribution gaussienne
-
titre : Desaccord relatif Laser - Résonnance de l'atome
label : domega
unités : w0
Désaccord relatif du laser
-
titre : Atome choisi
label : atome
Nom de l'atome refroidi
Valeurs possibles :
Liste des paramètres de sortie de l'applet
-
titre : Nombre d'atomes avec une vitesse v
label : Nv
-
titre : vitesse des atomes
label : v
unités : m/s
-
label : Nvi
-
label : Fv
-
label : x
-
label : Nx
-
label : Nxi
Introduction
Cette applette généralise à un grand nombre d'atomes (ce qu'on appellera par la suite une "population d'atomes") ce que l'appliquette précédente permettait de faire avec un seul atome.
Nous vous conseillons donc de bien vous familiariser avec l'appliquette "Atome Unique" avant de regarder celle-ci dans le détail, votre compréhension des phénomènes physiques en jeu n'en sera que meilleure !
D'autre part, les notions présentes dans cette applet sont les mêmes que dans l'applet "Atome Unique", nous vous renvoyons donc au cours qui y est présenté pour tous les détails de physiques utiles.
-
Objectifs
-
Cette applet permet de suivre l'évolution de la vitesse d'une population d'atomes ne pouvant se déplacer que selon une direction et soumis à deux rayonnement LASER de sens opposés.
Mode d'emploi de l'applet
Présentation
Dans cette applet, nous considérons donc un groupe d'atomes dont les vitesses sont tirées aléatoirement selon une gaussienne. Le nombre d'atomes ainsi que la moyenne et l'écart-type de la distribution de vitesse sont définis par l'utilisateur.
Dans la simulation, les atomes ne peuvent se déplacer que selon un axe et sont soumis à deux rayonnements LASER (un dans chaque direction) dont le désaccord (c'est à dire la différence entre la fréquence des photons du LASER et la fréquence de la transition atomique considérée) peut être réglée par l'utilisateur. La figure ci-dessous représente cette situation.
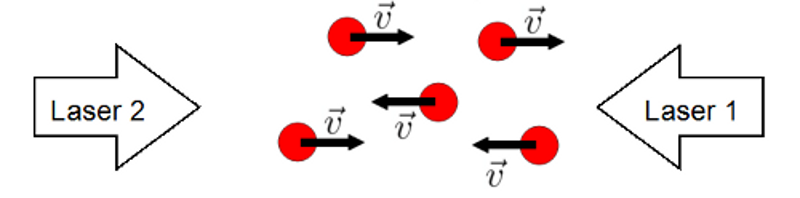
Schéma de la situation modélisée par l'applet "Population d'atomes".
C. Charignon & C. Collet
Paramètres choisis par l'utilisateur
Dans cette applet, l'utilisateur peut fixer quatre grandeurs :
-
Nombre d'atomes
-
Il correspond au nombre d'atomes qu'il y aura dans la population. Plus ce nombre est grand et meilleure est la simulation, car les statistiques se feront sur un grand échantillon. Cependant, le temps de calcul est aussi proportionnel au nombre d'atomes, il faut donc trouver un juste milieu.
Un population de quelques 10 000 atomes représente un compromis acceptable. Vous pouvez néanmoins essayez de monter jusqu'à 100 000 atomes si vous en avez envie !
-
Vitesse initiale moyenne
-
Elle correspond à la vitesse d'ensemble de la population. Pour un gaz au repos (typiquement l'air d'une pièce) cette vitesse est nulle. Comme c'est une vitesse, elle s'exprime en m/s (mètre par seconde).
-
Ecart-type de la distribution de vitesse
-
Il s'agit de la dispersion de vitesse autour de la vitesse moyenne. Il caractérise donc la largeur de la distribution de vitesse de la population d'atomes. Là aussi cette grandeur d'exprime en m/s (mètre par seconde).
-
Désaccord relatif entre le LASER et la fréquence de résonance de l'atome
-
Il est lié à la vitesse de l'atome pour laquelle la force qu'il subit du faisceau LASER sera maximale. En changeant sa valeur, vous devriez donc voir se déplacer la valeur de la vitesse pour laquelle il n'y a quasiment aucun atome, signe que la force qu'ils subissent à ce moment là est maximale.
Ce désaccord s'exprime en partie par million de la fréquence de résonance de l'atome. Si vous choisissez 1 pour cette valeur, cela veut dire que les photons émis par le LASER auront une fréquence
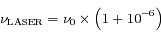
; où
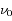

est la fréquence de résonance de l'atome.
-
Ensemble : thermique
-
Ce menu vous permet de réinitialiser les différents champs à des valeurs typiques. Ainsi le choix "thermique" donne les conditions d'un gaz à température ambiante avec un LASER accordé de telle manière que son maximum d'efficacité soit bien visible.
-
Atome choisi
-
Vous ne pouvez pour l'instant que choisir l'atome de Rubidium, dont la transition active est celle qui a une longueur d'onde de 780 nm et qui correspond au passage de l'état 2 S 1/2 à l'état 2 P 3/2.
D'autres atomes seront peut être ajoutés à l'avenir, mais le principe restera le même.
Les différents graphes proposés
-
Distribution des vitesses
-
Cela permet de suivre l'évolution de la distribution de vitesse au cours du temps. L'axe des abscisses représente donc les vitesses
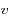
que peuvent avoir les atomes et l'axe des ordonnées le nombre d'atomes ayant cette vitesse
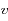
, à une petite quantité
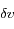
près, qui correspond à la largeur des histogrammes.
Les histogrammes bleus représentent l'évolution de la distribution de vitesses des atomes au cours de la simulation. Nous avons choisi de représenter également la distribution initiale de vitesses, qui apparait elle en rouge. Nous trouvons que cela permet de mieux suivre l'évolution de la distribution de vitesses.
Notons enfin que la largeur des histogrammes varie au cours de la simulation et qu'il peut donc y avoir plus ou moins d'atomes par tranche de vitesse. Cela peut donner l'impression (notamment sur la distribution initiale de vitesses) que le nombre d'atomes augmente au cours de la simulation, ce qui n'est bien sur pas le cas !
-
Distribution des positions
-
Ce choix permet de suivre "l'éparpillement" spatial des atomes au cours du temps. L'axe des abscisses représente donc la position
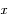
d'un atome et l'axe des ordonnées, le nombre d'atomes ayant cette position
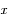
, à
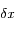
près.
On considère que les atomes sont tous au même endroit au départ, c'est à dire en
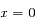
puis qu'ils s'en éloignent puisqu'ils ont une vitesse non nulle. Comme pour les vitesses, la distribution initiale des positions est tracée en rouge et la bleue correspond à son évolution au cours du temps.
Cette représentation permet de bien se rendre compte du ralentissement des atomes au cours du temps car on voit nettement les deux "pics" (un pour chaque direction possible de la vitesse) d'atomes se déplacer de plus en plus lentement avant de s'immobiliser lorsque tous les atomes ont été stoppés par les faisceaux LASER.
Exemple d'utilisation
Mise en évidence d'une vitesse pour laquelle la force exercée par le LASER est maximale
Prenons une population de 10 000 atomes, on verra ainsi aisément la valeur de la vitesse pour laquelle il y a beaucoup moins d'atomes. Penons également une vitesse moyenne initiale non-nulle, à 100 m/s, pour que la distribution initiale ne nous cache pas la partie du graphe intéressante. Enfin, prenons une dispersion de vitesse de 20 m/s (la valeur par défaut).
Quel est le lien entre le désaccord que vous pouvez régler et la vitesse pour laquelle la force exercée par le LASER est maximale ? Pour maximiser la force, il faut que son dénominateur soit le plus petit possible, et donc que
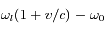
soit nul. Donc, vu la définition de
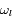
et du désaccord, on aura la force maximale pour la vitesse
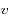
telle que :
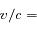
désaccord. Cela est illustré par la figure ci-dessous, pour laquelle le désaccord vaut 0.1.
Illustration de l'influence du désaccord
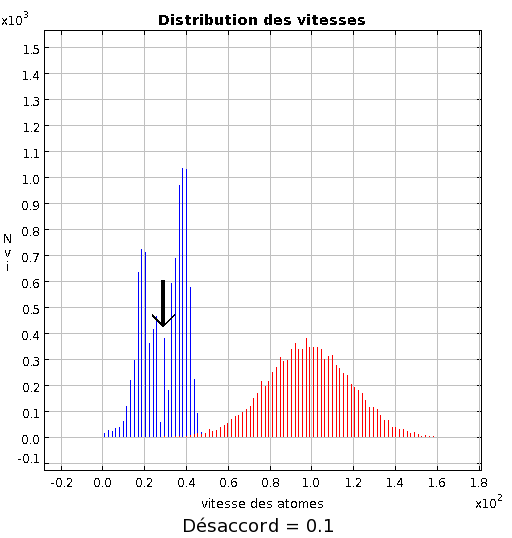
Le désaccord de 0.1 mène à une force maxiamale pour la vitesse 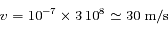
C. Charignon & C. Collet

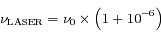 ; où
; où 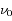
 est la fréquence de résonance de l'atome.
est la fréquence de résonance de l'atome.
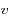 que peuvent avoir les atomes et l'axe des ordonnées le nombre d'atomes ayant cette vitesse
que peuvent avoir les atomes et l'axe des ordonnées le nombre d'atomes ayant cette vitesse 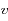 , à une petite quantité
, à une petite quantité 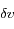 près, qui correspond à la largeur des histogrammes.
près, qui correspond à la largeur des histogrammes.
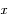 d'un atome et l'axe des ordonnées, le nombre d'atomes ayant cette position
d'un atome et l'axe des ordonnées, le nombre d'atomes ayant cette position 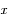 , à
, à 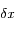 près.
près.
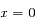 puis qu'ils s'en éloignent puisqu'ils ont une vitesse non nulle. Comme pour les vitesses, la distribution initiale des positions est tracée en rouge et la bleue correspond à son évolution au cours du temps.
puis qu'ils s'en éloignent puisqu'ils ont une vitesse non nulle. Comme pour les vitesses, la distribution initiale des positions est tracée en rouge et la bleue correspond à son évolution au cours du temps.
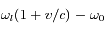 soit nul. Donc, vu la définition de
soit nul. Donc, vu la définition de 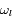 et du désaccord, on aura la force maximale pour la vitesse
et du désaccord, on aura la force maximale pour la vitesse 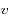 telle que :
telle que :
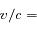 désaccord. Cela est illustré par la figure ci-dessous, pour laquelle le désaccord vaut 0.1.
désaccord. Cela est illustré par la figure ci-dessous, pour laquelle le désaccord vaut 0.1.