Refroidissement de la Lune
Auteurs:
Andy Richard, Melody Sylvestre
Date de création :
19 octobre 2010
Table des matières
Introduction
Le but de cette appliquette est de simuler le refroidissement d'un corps sphérique homogène à partir de différentes conditions initiales. Cela permettra, en fixant convenablement les paramètres d'entrées, de modéliser le refroidissement de la Lune.
Contexte observationnel
La Lune s'est formée lors d'une collision entre la Terre et un corps massif il y 4,526 milliards d'années. Ensuite, elle a aussi subi de nombreux chocs dus à des astéroïdes et des météorites, en nombre important dans le système solaire primitif. De plus, les matériaux dont elle est composée contiennent des éléments radioactifs. Tous ces phénomènes constituent la source de chaleur de la Lune. Elle est donc plus chaude que son environnement et se refroidit lentement. Ce refroidissement est toujours visible aujourd'hui puisque de récentes observations montrent de longues failles, causées par la contraction liée à la perte de chaleur.
Failles sur la Lune

Figure 1 : Les flêches désignent de petits cratères d'environ 40 m de diamètre. Dans le cadre supérieur, on voit que la moitié du cratère a disparu ce qui indique que la faille est ultérieure à l'impact.
NASA/Goddard/Arizona State University/Smithsonian
(
http://www.nasa.gov/mission_pages/LRO/news/shrinking-moon.html)
Méthode
On veut étudier l'évolution de la température de la Lune au cours du temps. Afin de simplifier le problème, on suppose qu'il s'agit d'une sphère parfaite et homogène. Pour cela, on utilise l'équation de diffusion de la chaleur en coordonnées sphérique. On la résout en utilisant l'algorithme de Crank-Nicholson (et la méthode des volumes finis). Cela nous permet de visualiser l'évolution du profil de température en fonction du rayon au cours du temps.
Rappels de cours
Dans ce problème, plusieurs grandeurs physiques interviennent. Ce paragraphe a pour but de les définir.
-
Conductivité thermique k
-
Il s'agit d'une grandeur propre à chaque matériau qui représente sa capacité à diffuser la chaleur à travers une surface sous l'effet d'un gradient de température. Son unité dans le sytème international est le W.m-1.K-1.
-
Masse volumique
-
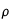 est le rapport entre la masse du corps et son volume. Son unité est le kg.m-3.
est le rapport entre la masse du corps et son volume. Son unité est le kg.m-3.
-
Enthalpie H
-
L'enthalpie est associée à l'énergie totale d'un système thermodynamique. Sa variation à pression constante est égale à la variation d'énergie interne du système à laquelle on ajoute le travail exercé par son environnement. Elle correspond à un flux de chaleur entrant ou sortant dû par exemple, à une réaction chimique. Son unité est le Joule.
-
Capacité calorifique à pression constante
-
Cp correspond à la quantité d'énergie qu'il faut fournir à un corps pour augmenter sa température de 1 Kelvin lors d'une transformation isobare. Son unité est le J.K-1.
Afin de comprendre le problème, on donne la définition des différents processus physiques qui entrent en jeu.
-
Convection
-
Il s'agit d'un mécanisme de transfert d'énergie par l'intermédiaire de déplacements de la matière dans le milieu. Elle se déplace du milieu le plus énergétique vers le moins énergétique et engendre des mouvements circulaires tels que ceux observés dans la croûte terrestre ou les étoiles.
-
Transfert Radiatif
-
A la différence de la convection, le transfert radiatif est un mécanisme de transfert d'énergie sans déplacement de matière. L'énergie est transportée sous forme de rayonnement électromagnétique et le flux émis par un corps est proportionnel à T4 (où T désigne la température à sa surface) selon la loi de Stefan-Boltzmann.
Explications
Diffusion de la chaleur dans un corps sphérique
Dans un corps quelconque, la diffusion de la chaleur est donnée par l'équation :
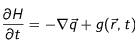
où
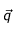
représente le flux de chaleur et
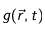
est un terme source.
H représente l'enthalpie du système.
Or :
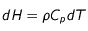
et
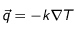
où
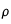
est la
masse volumique du corps, C
p est la
capacité calorifique à pression constante.
Si on néglige le terme source et si le corps est sphérique, on obtient :
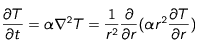 (1)
(1)
où r est la coordonnée radiale et
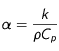
.
Conditions limites
Initialement, on suppose que la température du corps sphérique est fixée à T
0 en tout point. Il est plongé dans un environnement de température T
ext. Ainsi l'évolution du profil de température dépend uniquement de la distance au centre r. L'équation
(1) présente une singularité en
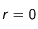
. Il faut donc définir une condition limite au centre. Ici, on impose
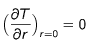
.
Pour traiter la singularité, on considère une petite sphère de rayon
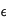
. On intègre l'équation
(1) sur ce domaine. On obtient :
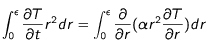 (2)
(2)
.
A l'extérieur de la sphère, la température vaut T
ext en tout point. A la surface de la sphère, différents mécanismes de transfert de température existent. Ici, nous nous intéresserons plus particulièrement à la
convection et au transfert radiatif. Ces processus influent sur l'évolution du système par l'intermédiaire des conditions à la surface. En effet, dans le cas de la convection, à la surface on a :
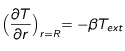 (3)
(3)
où R est le rayon du corps et
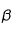
est le coefficient de convection à sa surface.
Si on a du transfert radiatif à la surface, la condition limite devient :
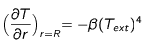 (a)
(a)
Traitement numérique
Afin de traiter numériquement ce problème, on utilise l'algorithme de Crank-Nicholson. Cela revient à discrétiser le temps et l'espace dans le problème. On introduit le pas de discrétisation spatiale h et de discrétisation temporelle k. T(r,t) devient alors T(i,j) où
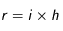
et
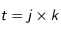
. Pour simplifier les calculs, on dédimensionne le problème de telle sorte que le rayon r varie entre 0 et 1 et
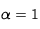
.
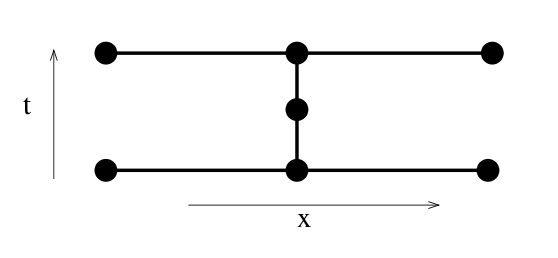
Figure 2 : Discrétisation spatiale et temporelle
Cela permet de calculer les dérivées en chaque point de la maille. La dérivée temporelle au milieu d'une maille s'écrit :
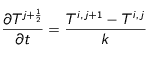 (4)
(4)
On procède de même avec
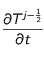
et avec les dérivées spatiales. La dérivée spatiale seconde au point
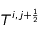
est la moyenne des dérivées spatiales secondes en j et en j+1.
Grâce à cela, on peut aussi discrétiser l'opérateur laplacien :
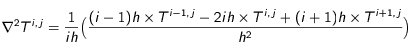
.
Grâce à
(4) et
(1), on a en posant
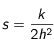
:
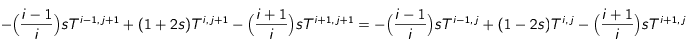 (5)
(5)
Au centre du corps, sur la sphère de rayon
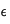
, si
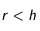
,
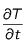
varie peu et on peut écrire :
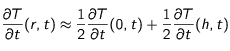 (6)
(6)
Ainsi, en insérant l'équation
(6) dans
(2), et en remplaçant
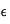
par
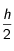
, on a :
![\Bigl [\Bigl(\frac{\partial T}{\partial t}\Bigl)_{r=0} +\Bigl(\frac{\partial T}{\part! ial t}\Bigl)_{r=h}\Bigl]\frac{h}{12}=\frac{1}{h}(T_1-T_0)](eq_tex_profilT_doc/equation32.png) (7)
(7)
où T
1 est la température de la première maille.
On insère l'équation
(4) dans l'équation (7) :
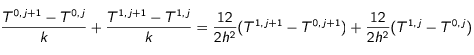 (8)
(8)
Si on pose
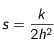
, on a finalement :
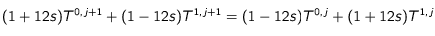 (9)
(9)
A la surface, par analogie avec l'équation
(4), la relation
(3) s'écrit alors :
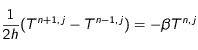
où T
n,j correspond à la température à la n
ième maille. On a l'expression de Tn+1,j en fonction de Tn-1,j et de Tn,j qu'on réinsère dans l'équation
(5).
On a alors, à la surface :
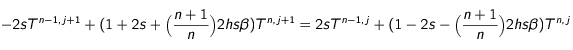 (10)
(10). En utilisant les équations
(9) pour le centre du système,
(10) pour le bord extérieur et
(5) entre ces deux limites, on obtient un système d'équations linéaires que l'on peut synthétiser sous la forme suivante :
Décomposition LU
On cherche à résoudre le système suivant:
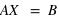
On va donc décomposer la matrice
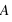
en un produit de deux matrices, l'une triangulaire inférieure
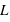
et l'autre en une matrice triangulaire supérieure
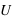
.


On a donc:
On se retrouve donc pour les éléments de la matrice
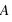
avec:
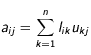
or si
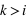
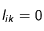
et si
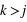
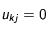
donc on se ramène à:
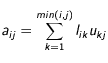
Cette expression nous donne
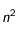
équations pour déterminer les
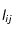
et
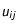
.
Mais les inconnues sont au nombre de ceux d'une matrice plus une diagonale, soit
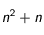
inconnues. Pour déterminer alors les coefficients, on pose tous les éléments diagonaux de
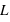
égaux à 1.
Donc dans le cas où
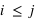
:
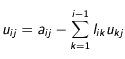
et pour
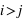
:
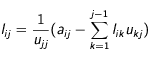
Il suffit alors de partir de
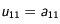
et de retrouver toutes les valeurs par
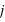
croissants pour un
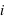
donné.
En reprenant le système à résoudre, on a donc:
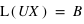
En posant
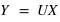
, on trouve alors:
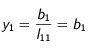
et pour
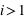
:
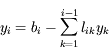
Et on retrouve
avec
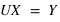
de la même façon:
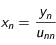
puis par valeurs décroissantes de
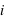
:
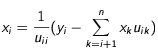
Dans notre cas la matrice
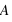
est tridiagonale donc on l'écrit:
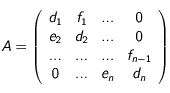
Et on peut simplifier les équations précédentes dans le cas de la détermination des matrices triangulaires:
par
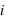
croissants:
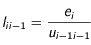
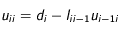
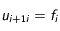
et avec
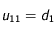
Puis par
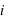
croissants:
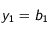
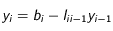
et par
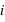
décroissants par la suite:
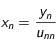
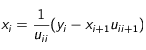
et on a ainsi inversé le système et résolu le système linéaire.
Détermination du profil théorique
Intérêt
La détermination d'un profil théorique est motivée par le fait que le profil observé dans le cas sans source semble auto-similaire , c'est à dire que la courbe semble identique et varie seulement avec un facteur lié au temps. C'est pourquoi on a tenté une approche avec une séparation des variables pour la température.
Méthode
On part du cas de l'équation de la chaleur adimensionnée sans termes sources définie par:
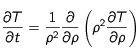
On fait donc l'hypothèse de la séparation des variables, d'où:
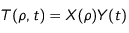
En insérant ce résultat dans l'équation de la chaleur, on obtient une équation de cette forme pour la fonction radiale:
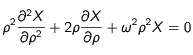
le oméga provenant d'une constante que l'on retrouve en développant les équations et qui est arbitraire.
En posant
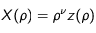
on obtient l'équation suivante:
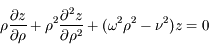
si on impose
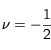
on retrouve cette forme pour les équations.
Les solutions
sont les fonctions de Bessel donc
peut s'écrire:
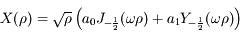
Les conditions aux limites de gradient de la température nul au centre et de variation de la température au bord proportionnelle (avec
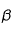
)à une température extérieure (voir cas précédent), impose comme condition pour le paramètre
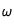
:
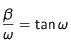
qui possède plusieurs solutions.
Dans le programme, ces valeurs sont déterminées par la méthode de Newton jusqu'à un certain ordre car la fonction tangente est périodique et donc l'équation possède plusieurs solutions. Par cette méthode on recherche les zéros de la fonction correspondante à la différence des deux membres.
On voit donc que la température est une somme de l'ensemble des solutions précédente avec la valeur de
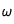
calculée par la méthode de Newton correspondante et en faisant le même travail pour la partie temporelle de la séparation des variables, on obtient finalement pour la température:
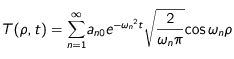
En imposant les conditions initiales pour la température égale à 1 pour tout
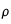
à t=0, on se retrouve avec un système linéaire à résoudre pour déterminer les coefficients
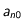
quand on tronque le développement à un certain ordre N. L'inversion de ce système par la méthode de la décomposition LU et de l'inversion qui en suit décrite plus haut permet de déterminer ces coefficients.
Une fois tous les paramètres obtenus, il suffit de calculer la valeur de la température en chaque point et à un instant t dans le programmme par la formule précédente de la température théorique obtenue et de l'afficher à l'écran.
Dans le cas théorique, le paramètre du flux
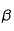
est limité à certaines valeurs car la sommation effectuée dans le programme est réalisée des valeurs les plus faibles supposée des coefficients aux plus grands et quand ce paramètre est trop grand les calculs sont faussés.
La courbe théorique sur le graphe est tracée en rouge et est proche du calcul numérique à certains moments et éloignée à d'autres, car notre hypothèse de séparation des variables n'est qu'une approximation résultante d'une constatation faite à partir du profil calculé par notre programme.
Diffusion avec sédimentation
Ici, nous souhaitons considérer le cas où la Lune possède une source radiative interne, dont les particules radioactives vont sédimenter vers le centre de l'astre, refroidissant la surface et entraînant la formation d'une croûte. Nous nous placerons dans un cas isotrope où les différentes grandeurs physiques ne dépendront donc que du temps et du rayon
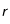
(coordonnées sphériques) par rapport au centre de l'astre.
Mise en équation du problème de sédimentation
En coordonnées cartésiennes :
Considérons les particules de la source radioactive. Deux phénomènes physiques sont alors à prendre en compte : d'une part la diffusion
des particules, d'autre part la sédimentation des particules les plus massives.
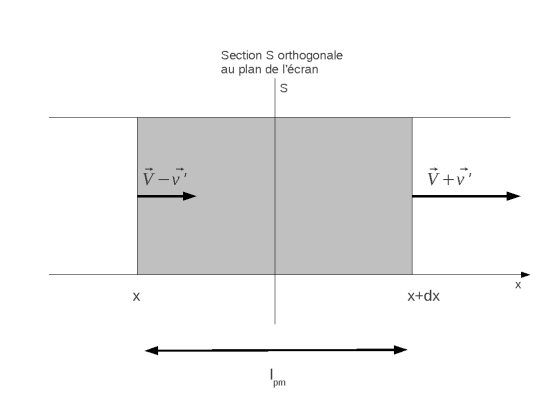
Figure 3 :Elément de fluide considéré pour la détermination des équations du mouvement
Supposons un flux de particules dans la direction des
positifs (
figure 3). Supposons que notre fluide se comporte comme un gaz parfait de particules se déplaçant toutes avec une vitesse moyenne égale à la vitesse thermique des particules,
. Appliquons le modèle du "
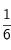
'' (c'est-à-dire, considérons que les particules se déplacent toutes selon les axes). Dans ce cas, le flux de particules à travers la section
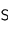
pendant
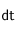
vaut :
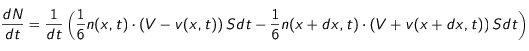
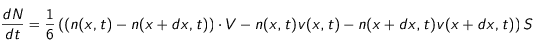
où
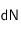
est le nombre élémentaire de particules traversant
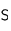
pendant l'intervalle de temps
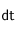
,
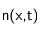
est la densité de particules en
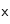
à l'instant
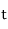
, et
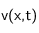
la vitesse des particules sédimentant.
Si l'on suppose que la distance typique séparant les particules en
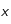
et
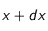
(autrement dit
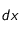
) est de l'ordre du libre parcours moyen
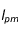
des particules, alors le flux de particules
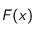
par unité de temps à travers la surface
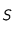
sera :
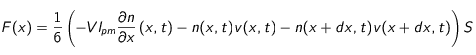
que l'on choisira de réécrire sous la forme :
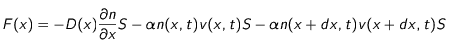
où
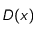
est le coefficient de diffusion des particules et peut dépendre de la position
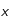
, et
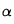
un coefficient que l'on peut assimiler au pourcentage de particules qui vont effectivement sédimenter dans la direction
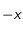
avec la vitesse
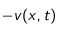
(en supposant, pour simplifier, que
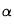
ne dépend ni de la position, ni du temps).
Si de plus, on émet l'hypothèse que le nombre de particules sédimentant (ainsi que leur vitesse de sédimentation) dans la direction
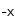
est le même en
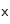
et
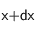
, alors l'expression du flux devient :
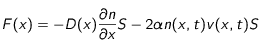
que l'on réécrira (en posant
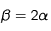
sans dimension) :
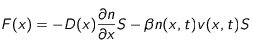 (11)
(11)
Avec
(11), on vérifie bien :
- d'une part, que le flux diffusif se fait bien des densités élevées vers les densités faibles (
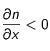
et donc
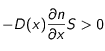
lorsque les densités élevées sont au centre)
- d'autre part, que le flux de particules sédimentant est bien dirigé vers le centre, des densités faibles vers les densités élevées
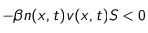
pour
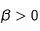
)
Note : Ceci permet donc de faire une simple vérification une fois la programmation faite, puisqu'on s'attendra alors, pour des valeurs extrêmes de 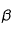
,
à obtenir soit de la sédimentation si 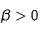
,
soit un phénomène de pseudodiffusion si 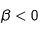 )
).
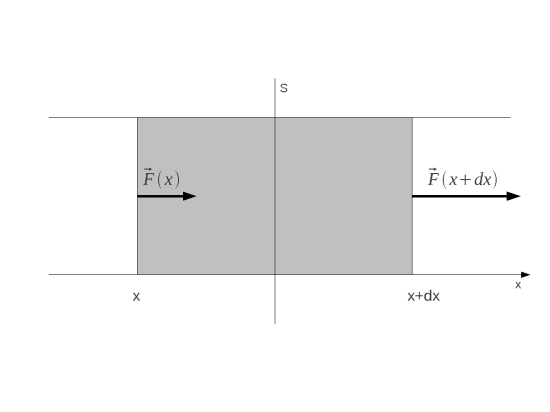
Figure 4 : Elément de fluide pour la conservation du nombre de particules dans le volume 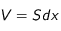
A l'aide de la
figure 4, nous allons établir l'équation différentielle pour
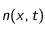
. Le nombre élémentaire de particules traversant une surface
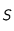
pendant un intervalle de temps
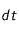
est :

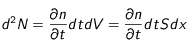 (12)
(12)
Le flux élémentaire
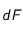
entre
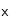
et
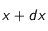
est :
![dF=F(x+dx)-F(x)={\frac{\partial F}{\partial x}}dx={\frac{\partial}{\partial x}\left[-D(x){\frac{\partial n}{\partial x}}-{\beta}n(x,t)v(x,t)\right]}Sdx](eq_tex_profilT_doc/equation133.png)
c'est-à-dire :
![dF=-\left[{\frac{\partial}{\partial x}}\left(D(x){\frac{\partial n}{\partial x}}\right)+{\beta}\frac{\partial\left(nv\right)}{\partial x}\right]Sdx](eq_tex_profilT_doc/equation134.png) (13)
(13)
La variation du nombre de particules dans le volume
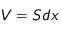
entre
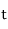
et
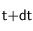
vaut :
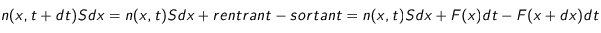
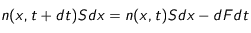 (14)
(14)
En utilisant
(12),
(13), et
(14), on obtient finalement l'équation
du problème :
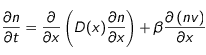
En coordonnées sphériques :
On considère un cas isotrope de sorte que
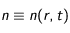
et
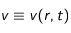
.
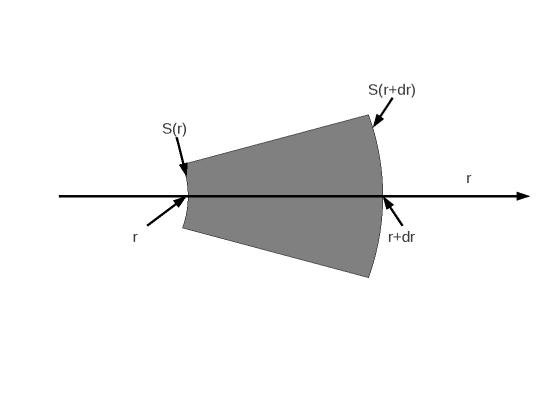
Figure 5 : Schéma descriptif du problème en coordonnées sphériques, avec symétrie sphérique
Finalement, après avoir remplacé
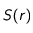
par son expression puis simplifié par
, on obtient :
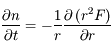
Ce qui conduit à l'équation suivante :
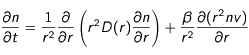 (15)
(15)
A présent, nous allons dédimensionner l'équation
(15) avant de lui appliquer l'algorithme de Crank-Nicholson. Tout d'abord, considérons deux constantes
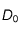
et
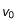
, grandeurs dimensionnées caractéristiques du coefficient de diffusion
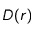
et de la vitesse de sédimentation des particules
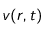
, telles que
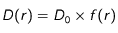
et
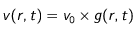
où
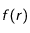
et
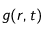
sont sans dimension.
Puis, appliquons les changements de variables suivants :
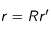
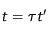
où
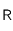
et
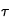
sont des grandeurs caractéristiques du problème (ici,
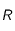
correspondrait au rayon de la source, et
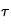
au temps caractéristique d'évolution de la densité). L'équation
(15) devient donc :
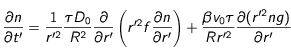
avec
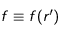
et
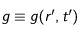
.
Enfin, choisissons
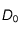
,
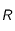
, et
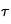
telles que
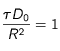
. Posons
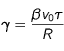
(notons que, comme
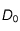
est en
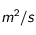
et que
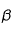
est sans dimension, l'homogénéïté pour les deux égalités est bien respectée).
L'équation adimensionnée est donc :
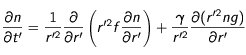 (16)
(16)
Par commodité, on notera pour la suite
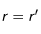
dans les équations
(
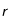
sans dimension).
Algorithme de Crank-Nicholson pour la sédimentation
On considère que le coefficient de diffusion et la vitesse moyenne de sédimentation des particules sont constants.
Ecriture de l'équation sous forme algorithmique
Pour ce cas, cela signifie que l'on prendra
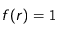
et
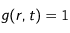
, de sorte que l'équation
(16) s'écrive :
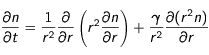 (17)
(17)
Pour appliquer Crank-Nicholson, nous fixons un pas spatial
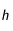
et un pas temporel
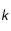
. Ensuite, il va s'agir d'établir l'expression discrétisée de l'équation précédente en
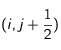
(indice spatial, indice temporel),
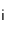
et
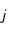
étant des entiers.
On a alors :
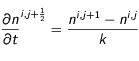 (18)
(18)
De la même façon, nous aurons pour une dérivée première spatiale :
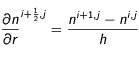 Note : Si jamais l'indice
Note : Si jamais l'indice 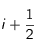 (respectivement
(respectivement 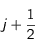 ) apparaît pour une variable, étant donné que l'on a discrétisé en nombres entiers de
) apparaît pour une variable, étant donné que l'on a discrétisé en nombres entiers de 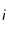 et de
et de 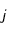 , alors on calculera la valeur en ce point comme étant la valeur moyenne du point suivant
, alors on calculera la valeur en ce point comme étant la valeur moyenne du point suivant 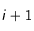 (respectivement
(respectivement 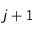 ) et du point précédent
) et du point précédent 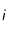 (respectivement
(respectivement 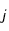 ).
Exemple :
).
Exemple :
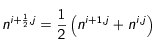 ou encore
ou encore
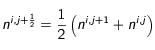

 de même pour toute dérivée partielle d'ordre
de même pour toute dérivée partielle d'ordre 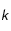 par rapport à une variable
par rapport à une variable 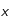 , on aura :
, on aura :
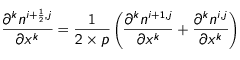 où
où 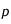 est le pas relatif à la variable
est le pas relatif à la variable 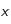 (dans notre cas,
(dans notre cas, 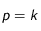 si
si 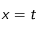 , ou
, ou 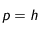 si
si 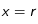
.
Notons que dans l'équation
(17) , le premier terme du membre de droite de l'égalité est en fait le laplacien en coordonnées sphériques. Pour des raisons de commodité, nous allons utiliser l'autre forme du laplacien sphérique d'une fonction
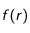
qui est :
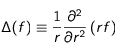
Dès lors, on obtient que :
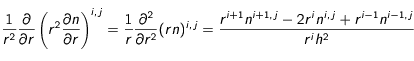

Il s'ensuit que le laplacien de
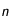
pris en
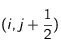
s'écrit :
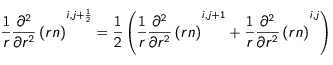
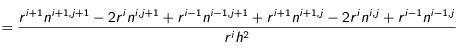 (19)
(19)


De même, on trouve que :
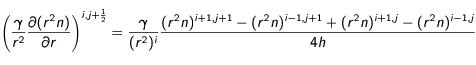 (20)
(20)
A présent, nous allons poser
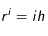
et
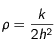
.
Note : 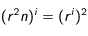 ainsi, on voit facilement que
ainsi, on voit facilement que 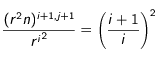
En prenant
(18),
(19) et
(20) que l'on injecte dans
(17), on obtient alors l'équation suivante :
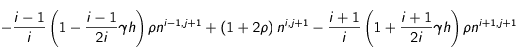
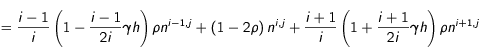 (21)
(21)
Détermination des conditions aux limites :
Pour résoudre complètement l'équation de départ
(17), il ne nous manque plus que les conditions aux limites.
-
Condition limite en
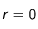 :
:
Pour obtenir une condition en 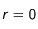 , nous allons procéder de la même façon que dans la cas sans source, c'est-à-dire en intégrant l'équation
(17) sur une sphère infinitésimale de centre 0 et de rayon
, nous allons procéder de la même façon que dans la cas sans source, c'est-à-dire en intégrant l'équation
(17) sur une sphère infinitésimale de centre 0 et de rayon 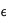 . Nous considèrerons qu'en
. Nous considèrerons qu'en 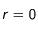 , le gradient de densité est nul pour n'importe quel temps
, le gradient de densité est nul pour n'importe quel temps 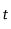 donc quelque soit
donc quelque soit 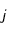 (
(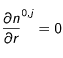 ).
).
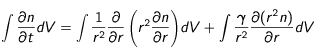
où 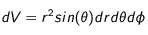 , ce qui donne, lorsque l'on considère un problème à symétrie sphérique (après simplification par
, ce qui donne, lorsque l'on considère un problème à symétrie sphérique (après simplification par 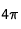 ):
):
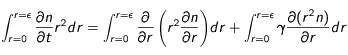 (22)
(22)
Notons que la seule différence avec le cas de diffusion seule (analogie avec l'équation de chaleur mais en remplaçant 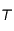 par
par 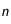 ) est la présence d'un second terme à intégrer dans le membre de droite de l'équation ci-dessus. Nous allons donc ne nous occuper que de l'intégration de ce terme et de son écriture via Crank-Nicholson, l'intégration des deux autres termes ayant déjà été faite dans la cas de l'équation de la chaleur avec diffusion seule.
) est la présence d'un second terme à intégrer dans le membre de droite de l'équation ci-dessus. Nous allons donc ne nous occuper que de l'intégration de ce terme et de son écriture via Crank-Nicholson, l'intégration des deux autres termes ayant déjà été faite dans la cas de l'équation de la chaleur avec diffusion seule.
On a :
![\int_{0}^{\epsilon} {\gamma \frac{\partial (r^2n)}{\partial r}}dr=\gamma \int_{0}^{\epsilon} {\partial (r^2n)}=\gamma {\left[r^2n\right]}_{0}^{\epsilon}=\gamma \epsilon ^2 n(\epsilon,t)](eq_tex_profilT_doc/equation247.png) (23)
(23)
En remplaçant (23) dans (22) et en utilisant le résultat pour la diffusion, on trouve alors :
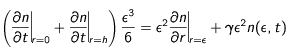
En reprenant la discrétisation précédente, et en choisissant 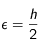 (milieu de la première maille, on obtient après une petite séance de gymnastique mathématique, la condition au centre :
(milieu de la première maille, on obtient après une petite séance de gymnastique mathématique, la condition au centre :
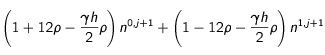
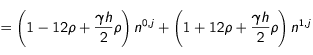 (24)
(24)
(où 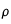 vaut toujours
vaut toujours 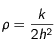 ).
).
-
Seconde condition aux limites :
Comme deuxième condition, nous prendrons la conservation de la masse des particules radioactives de la source, 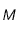 :
:
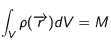
Comme nous considérons un cas isotrope, nous avons 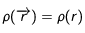 et donc en intégrant sur les deux angles
et donc en intégrant sur les deux angles  et
et  :
:
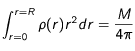 ou encore, avec le changement de variable
ou encore, avec le changement de variable 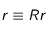 :
:
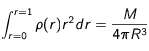
Ce qui, discrétisé de la même façon que précédemment et en utilisant la méthode des trapèzes peut se réécrire :
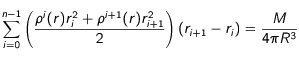
A partir de cette expression, on choisira de mettre la deuxième condition sous la forme suivante, (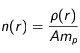 , où
, où 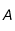 correspond au nombre de nucléons de l'élément radioactif et
correspond au nombre de nucléons de l'élément radioactif et 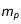 à la masse d'un proton ; rappelons que
à la masse d'un proton ; rappelons que 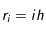 ) donnant une condition en
) donnant une condition en 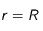 :
:
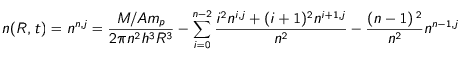 (23)
(23)
On remarque que dans la somme, les termes en 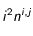 et en
et en 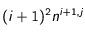 se ressemblent, reprenons-les et essayons d'arranger la somme différemment :
se ressemblent, reprenons-les et essayons d'arranger la somme différemment :
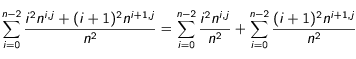
Prenons le membre en 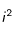 et appliquons-lui le changement de variable suivant :
et appliquons-lui le changement de variable suivant : 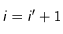 . Ce terme se réécrit donc :
. Ce terme se réécrit donc :
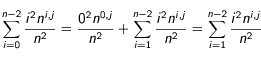
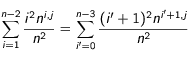
ce qui donne en utilisant le changement 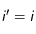 :
:
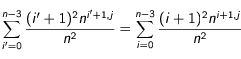
En remarquant que :
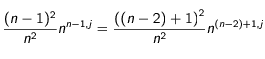
on obtient :
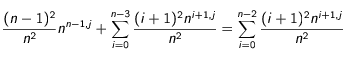
D'où finalement, on en déduit l'expression simplifiée de (23) :
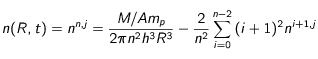
que l'on pourra réécrire (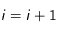 ) :
) :
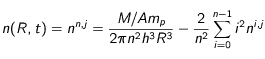
c'est-à-dire :
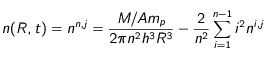 (25)
(25)
puisque 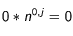 .
.
En utlisant (21), (24) et (25), on peut alors résoudre l'agorithme
numériquement.
Note : Un petit calcul rapide nous permet d'avoir une idée de la densité d'élément radioactif que l'on peut espérer trouver pour une masse donnée de cet élément. Partons d'un état initial uniforme, dans ce cas, dans ce cas, on a directement (en utilisant le fait que 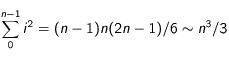 ,
, 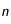 suffisament grand) :
suffisament grand) :
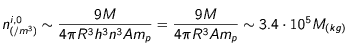
lorsque l'on considère de l'uranium (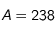 ) avec
) avec 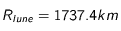 ,
, 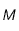 étant la masse totale d'uranium à l'intérieur de la Lune que
l'utilisateur pourra choisir.
étant la masse totale d'uranium à l'intérieur de la Lune que
l'utilisateur pourra choisir.
Prise en compte de l'élément radioactif dans l'équation de chaleur
Equation de la chaleur avec terme source
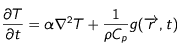
où
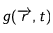
est le terme source. Rappelons que
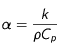
est la diffusivité thermique.
Le terme source correspond en fait à l'énergie que l'élément radioactif peut transmettre au milieu et pourra donc être caractérisé par la chaleur massique de cet élément. On peut donc exprimer ce terme source ainsi :
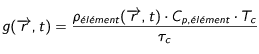
où
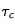
correspondrait au temps caractéristique nécessaire pour qu'un élément radioactif à la température
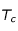
présent dans un volume
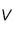
avec une densité
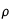
transfère une densité d'énergie
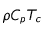
au milieu qui l'entoure. On sait que
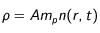
où
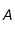
représente le nombre de nucléons de l'élément radioactif (en effet, puisque
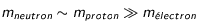
, on peut assimiler la masse atomique de l'élément à
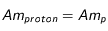
). Par ailleurs, compte-tenu du fait que le volume considéré est celui de la Lune et que l'on a fait l'hypothèse d'un problème à symétrie sphérique, on peut alors réécrire le terme source sous la forme suivante :
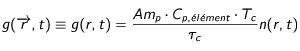
L'équation
(25) devient donc :
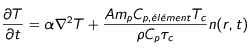
où l'on vérifie bien que le terme source nouvellement écrit a bien la dimension d'une température par unité de temps.
Si l'on reprend alors le même dédimensionnement que dans le cas de la diffusion thermique sans source, on obtient alors :
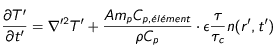 (26)
(26)
où
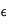
représente la "magnitude'' de
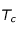
une fois dédimensionnée et est positif ;
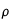
correspond à la masse volumique du milieu et donc ici à la masse volumique de la Lune (
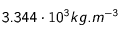
) ;
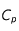
ainsi que
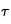
et
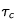
n'étant a priori pas connus, on choisira de prendre le paramètre libre
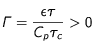
homogène à des
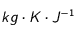
dont la valeur sera définie par l'utilisateur. En utilisant à présent les valeurs des différentes grandeurs connues (et que
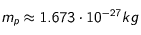
),
(26) donne :
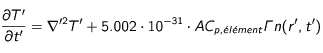 (27)
Note : Dans l'équation (27), on pourrait penser que le coefficient en
(27)
Note : Dans l'équation (27), on pourrait penser que le coefficient en 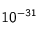 fera que le terme source ne changera absolument rien. Voici un petit calcul qui montre que cette intuition est fausse. Dans notre modélisation incluant un élément radioactif minoritaire, il
faut bien faire attention à la signification de minoritaire. Supposons que cet élément soit de l'uranium 238, minoritaire signifie que son
abondance Ab est faible par rapport à celle de l'élément prépondérant. Appelons
fera que le terme source ne changera absolument rien. Voici un petit calcul qui montre que cette intuition est fausse. Dans notre modélisation incluant un élément radioactif minoritaire, il
faut bien faire attention à la signification de minoritaire. Supposons que cet élément soit de l'uranium 238, minoritaire signifie que son
abondance Ab est faible par rapport à celle de l'élément prépondérant. Appelons 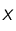 de masse
de masse 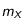 et de nombre de nucléons
et de nombre de nucléons 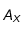 l'élément le plus abondant de la Lune, et supposons que l'abondance d'uranium 238 soit très faible :
l'élément le plus abondant de la Lune, et supposons que l'abondance d'uranium 238 soit très faible :
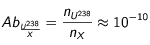 La masse totale d'élément
La masse totale d'élément 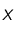 au sein de la Lune est donc :
au sein de la Lune est donc :
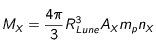
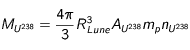
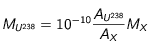 Si l'élément X est massivement majoritaire, on peut alors supposer que l'essentiel de la masse de la Lune vient de cet élément et que donc
Si l'élément X est massivement majoritaire, on peut alors supposer que l'essentiel de la masse de la Lune vient de cet élément et que donc 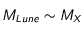 , dès lors, nous avons :
, dès lors, nous avons :
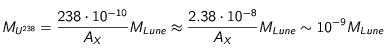 si l'on suppose que le nombre de nucléons de l'élément majoritaire n'est pas très grand devant 1. Avec
si l'on suppose que le nombre de nucléons de l'élément majoritaire n'est pas très grand devant 1. Avec 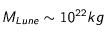 donc
donc 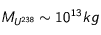 , on trouve finalement une densité d'élément radioactif :
, on trouve finalement une densité d'élément radioactif :
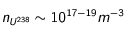 On obtient donc un terme source de l'ordre de :
On obtient donc un terme source de l'ordre de :
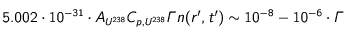 On peut voir que dans le programme, des valeurs pour le terme source (dans l'équation dédimensionnée) de l'ordre de
On peut voir que dans le programme, des valeurs pour le terme source (dans l'équation dédimensionnée) de l'ordre de 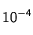 minimum ont un effet nettement visible sur la température, ce qui implique de choisir
minimum ont un effet nettement visible sur la température, ce qui implique de choisir 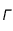 suffisamment grand (
suffisamment grand (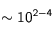 ) si l'on prend une abondance d'uranium aussi faible. On pourra donc prendre des valeurs faibles de
) si l'on prend une abondance d'uranium aussi faible. On pourra donc prendre des valeurs faibles de  pour des masses d'uranium plus grandes, et jouer avec les valeurs de ce paramètre pour une masse
donnée.
pour des masses d'uranium plus grandes, et jouer avec les valeurs de ce paramètre pour une masse
donnée.
Exemple d'utilisation
Corps plongé dans un environnement froid
Supposons une Lune de température homogène t0 à t=0 plongé dans un environnement plus froid. Le corps va donc se refroidir en dégageant de la chaleur de façon radiative au niveau de sa surface. En utilisant l'applette "Source manuelle" et une valeur de 10 pour le paramètre libre "q", tous les autres paramètres étant gardés à leurs valeurs par défaut, on accélère le processus de refroidissement de la surface et on obtient le résultat suivant au bout d'un temps assez court :
Corps plongé dans un environnement froid
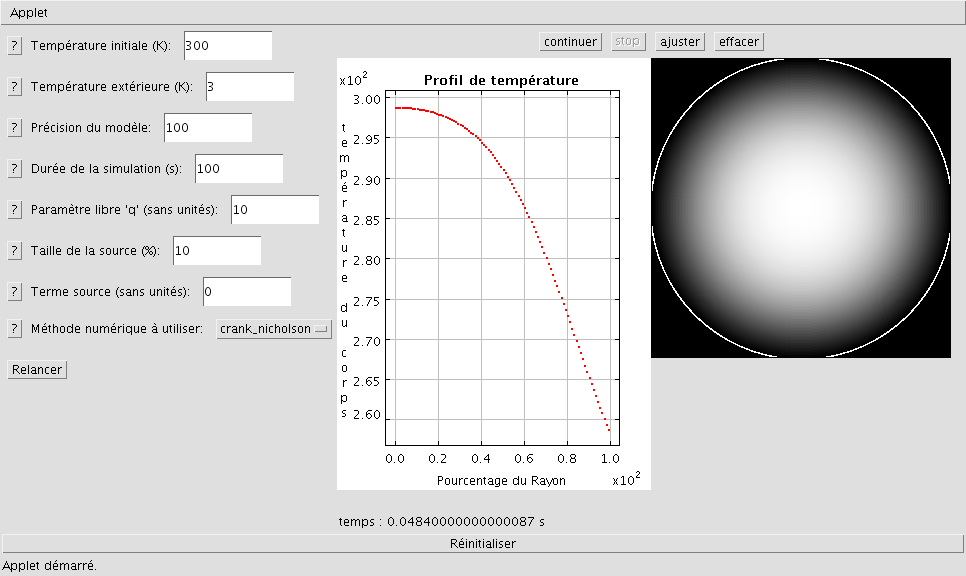
Affichage du refroidissement d'un corps. Les zones les plus chaudes sont en blanc, les plus froides en noir. On observe donc un refroidissement progressif en direction du centre du corps.
Il est également possible de tracer pour ce même corps l'évolution du flux de chaleur à la surface en parallèle avec le profil de température :
Affichage du flux et du profil de température
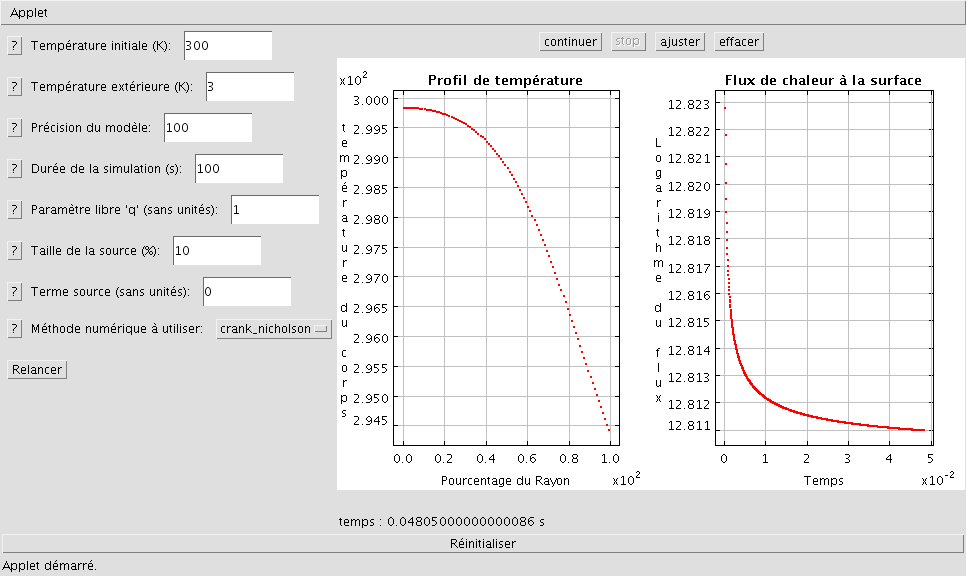
On observe une décroissance du flux à la surface liée au refroidissement de celle-ci.
Corps froid plongé dans un environnement chaud
En inversant le problème, on peut observer l'évolution du réchauffement du corps. Il suffit pour cela de mettre une température extérieure supérieure à la température interne, prenons par exemple Text=300K et To=3K. On observe l'évolution suivante :
Réchauffement d'un corps froid
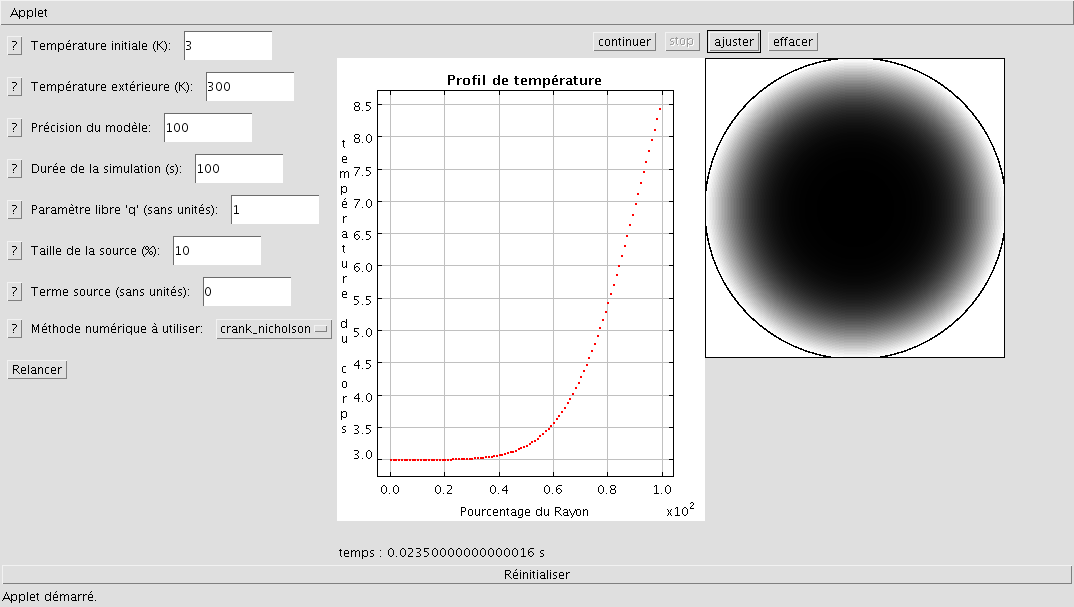
On observe une évolution similaire à celle du refroidissement, avec cette fois les températures les plus élevées à la surface (donc la couleur blanche) et les plus faibles au centre (couleur noire).
Corps contenant une source de chaleur au centre
En utilisant l'applette intitulée "Source Manuelle", on peut simuler le profil de température d'un corps contenant une source de chaleur au centre. Cette source est représentée par un flux de chaleur constant dont la valeur est comprise dans le champ "terme source" (qui n'a pas de réelle signification physique) et la taille est exprimée en pourcentage du rayon du corps. On peut par exemple imaginer une Lune contenant un noyau radioactif qui émet une quantité de chaleur constante. En prenant par exemple une source dont la taille représente 20% du rayon du corps, avec un terme source de 0.001, on obtient le résultat suivant:
Corps avec source au centre
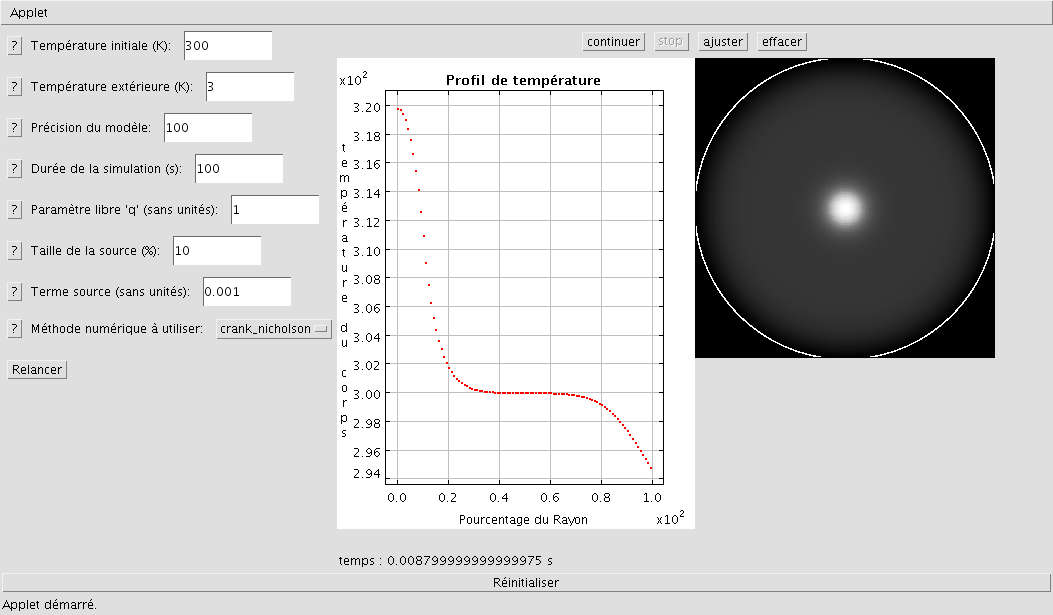
Affichage du profil de température et de l'image du corps avec source centrale. Les températures les plus chaudes sont en blanc, et les plus froides en noir. On observe bien la source au centre en blanc, le milieu du corps en gris foncé à température "moyenne", et le bord et l'extérieur en noir pour des températures plus froides.
Courbe théorique du problème de diffusion
Il est également possible via l'applette "Analytique-Numérique" d'effectuer une comparaison entre la solution analytique et la modèle numérique pour un problème de diffusion de la chaleur en sphérique. En gardant les paramètres initiaux de l'applette, on obtient au bout d'un temps d'execution assez court :
Comparaison entre modèle numérique et solution analytique
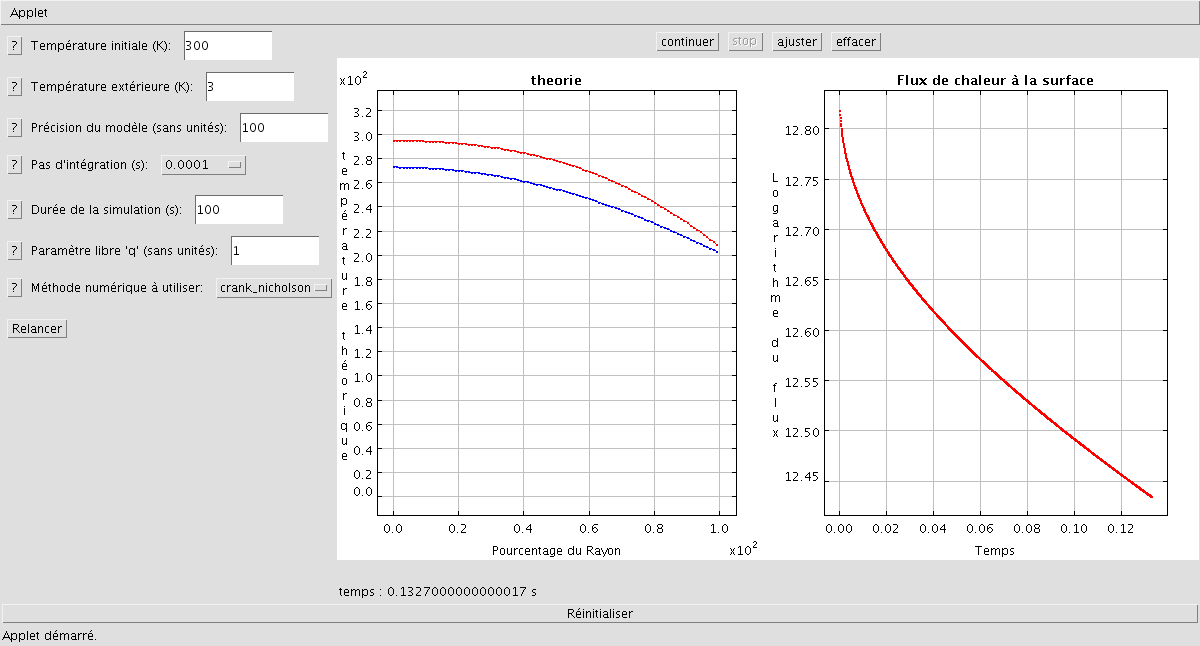
Affichage de l'écart entre théorie et modèle numérique, accompagné de la courbe de flux à la surface. On remarque un écart entre le modèle et la théorie. Ceci est lié aux approximations de la théorie qui ne permettent donc pas de coller au modèle numérique plus complet, cependant au bout d'un temps "infini", les deux courbes donnent les mêmes solutions.
Corps avec sédimentation de source radioactive
Un modèle plus réaliste de Lune suppose une sédimentation de la source au sein du corps sphérique. Pour cela, l'applette "Sédimentation" permet de modéliser le profil de température du corps en fonction de l'élément radioactif choisi, de sa masse en kilogramme et d'un paramètre de sédimentation. En imaginant une masse de
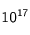
kg d'uranium 238 en "suspension" à l'intérieur de la Lune, avec un paramètre de sédimentation de 10, on observe l'évolution suivante :
Affichage du corps tenant compte de la sédimentation
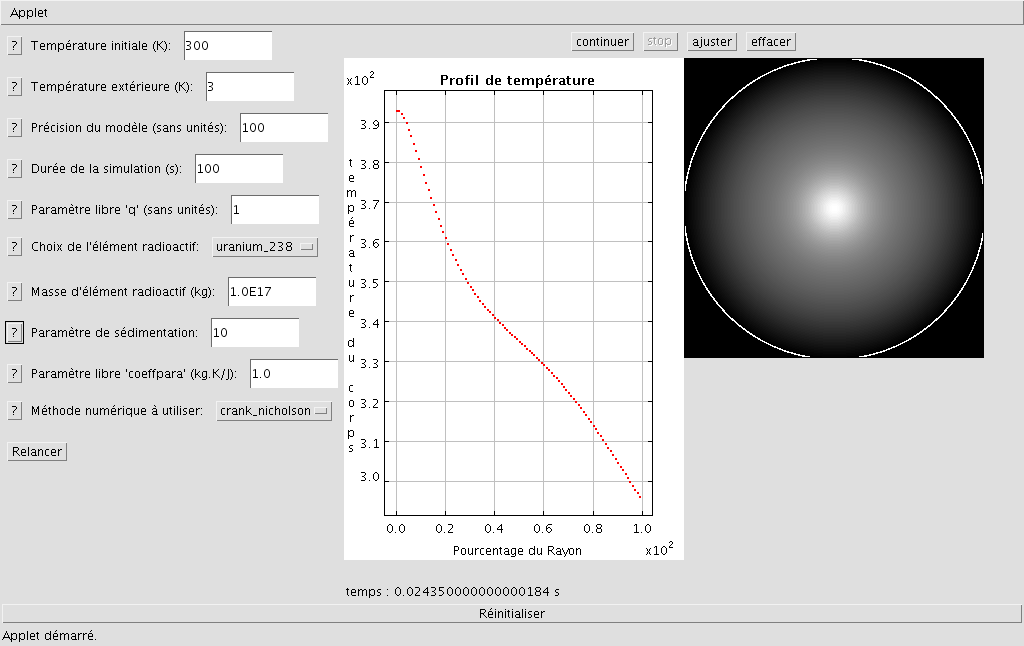
Affichage du profil de température tenant compte de la sédimentation de l'élément radioactif vers le centre du corps. On remarque une très nette augmentation de la température au centre du corps lié à l'apport de matière radioactive "chaude" au noyau.
On notera également la différence de profil avec le cas du corps avec source de chaleur au centre. Dans le cas de la sédimentation, la différence entre noyau, "manteau" et surface est moins prononcée. La source est plus diffuse puisqu'en cours de sédimentation et nous donne donc un profil de température moins brut. On suppose cependant qu'au bout d'un temps infini, les deux profils coïncident. Il est également possible pour le cas de la sédimentation de tracer le profil de densité et le flux de chaleur à la surface, ce qui nous donne pour les mêmes paramètres qu'auparavant:
Affichage du profil de densité et du flux
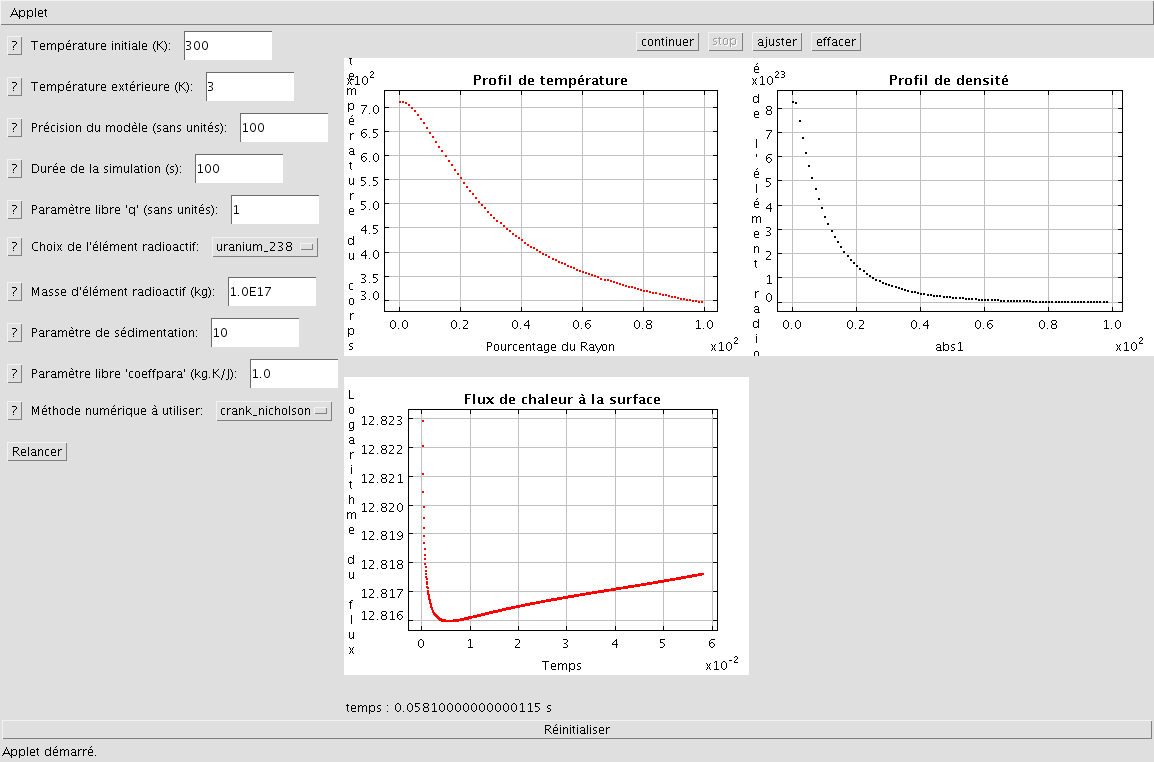
On note ici l'augmentation importante de la densité en r=0 ce qui traduit bien le phénomène de sédimentation de l'élément radioactif. On observe également une hausse du flux au bout d'un certain temps qui traduit l'augmentation globale de température du corps lié au terme source qui s'exprime ici sous forme de sédimentation.
Liste des paramètres d'entrée de l'applet
-
titre : Température initiale
label : to
unités : K
Température initiale du corps
-
titre : Température extérieure
label : text
unités : K
Température extérieure
-
titre : Précision du modèle
label : nbpoints
unités : sans unités
Précision du modèle
-
titre : Durée de la simulation
label : tf
unités : s
Temps de fin d'intégration
-
titre : Paramètre libre 'q'
label : q
unités : sans unités
Paramètre libre qui permet de régler la variation du flux de chaleur, au niveau de la surface lunaire, échangé avec le milieu extérieur.
-
titre : Choix de l'élément radioactif
label : element
Ce paramètre permet de choisir le type d'élément radioactif que l'on veut considéré comme source de chaleur, choix parmi trois possiblités d'éléments radioactifs trouvés en surface de la Lune :
-uranium 238, de période 4.46*10^9 ans
-thorium 232, de période 14.05*10^9 ans
-potassium 40, de période 1.3*10^9 ans
Valeurs possibles :
uranium_238 thorium_232 potassium_40
-
titre : Masse d'élément radioactif
label : masse
unités : kg
Masse de l'élément radioactif considérée, à l'intérieur de la Lune, qui sera utilisée pour établir sa densité initiale uniforme (ainsi que pour l'équation de conservation de la masse).
Lorsque vous changer la valeur de la masse, ne paniquez pas si vous ne voyez plus de points sur le graphe de la densité, c'est simplement que vous avez changé la masse suffisamment pour que l'échelle initiale du graphe ne soit plus adaptée aux valeurs de densités, vous n'avez alors qu'à appuyer sur 'ajuster' et la magie opèrera...
A noter qu'une masse minimale à considérer devrait être de l'ordre de 10^13 kg, ceci correspond à ce que l'on trouverait pour de l'uranium 238 d'abondance 10^-10 par rapport à un élément majoritaire non-radioactif constituant la Lune dont le nombre de nucléons serait de l'ordre de l'unité (dizaine de nucléons tout au plus); et dans ce cas, une valeur de coeffpara de l'ordre de 10^3 ou 4 serait suffisante pour observer les effets de cet élément radioactif sur la Lune. La valeur de 10^19 kg correspond à une abondance en élément radioactif de 10^-4.
Valeurs possibles :
1.0E13 1.0E14 1.0E15 1.0E16 1.0E17 1.0E18 1.0E19
-
titre : Paramètre de sédimentation
label : gamma
Paramètre de sédimentation.
La magnitude de ce paramètre reflète la magnitude du rapport entre diffusion et sédimentation.
Remarque : si ce terme est grand devant 1 en valeur absolue, cela signifie que les effets seront essetiellement dûs à la sédimentation.
Ce paramètre ne peut pas être négatif (sédimentation vers l'extérieur).
-
titre : Paramètre libre 'coeffpara'
label : coeffpara
unités : kg.K/J
Paramètre libre d'unité : kg.K.J^-1
Ce paramètre est en fait homogène à l'inverse d'une capacité calorifique massique à pression constante. Il est égal à un rapport de temps caractéristiques d'échange d'énergie (l'un caractéristique de l'élément radioactif, l'autre du milieu interne) multiplié par l'inverse de la capacité calorifique massique Cp du milieu interne de la Lune. Il incorpore également un coefficient représentant un rapport de températures (température effective normalisée d'échange thermique caractérisant l'élément radioactif).
Pour cela, parce ces grandeurs ne sont pas connues, on le laisse comme paramètre libre.
Remarque :
-c'est un paramètre positif;
-pour des valeurs de masse d'élément radioactif inférieures à 10^13 kg, les valeurs de ce paramètre nécessaires pour voir les effets de l'échange de chaleur venant de cet élément sont de l'ordre de 10^3 à 10^4 minimum (pour l'uranium ou le thorium); mais ceci dépend aussi de l'élément radioactif considéré, par exemple, pour le cas du potassium, on peut observer les effets de source de chaleur à partir de valeurs plus faibles que pour l'uranium.
-
titre : Méthode numérique à utiliser
label : methode
Permet de choisir la méthode numérique à utiliser pour resoudre l'équation de la chaleur.
'Crank_Nicholson' réfère à la méthode numérique du même nom.
'Rien' sert à ne pas résoudre les équations, et sert de valeur par défaut.
Valeurs possibles :
crank_nicholson rien
Liste des paramètres de sortie de l'applet
-
titre : température du corps
label : t
unités : K
-
titre : Densité de l'élément radioactif
label : n
unités : m^-3
-
titre : Pourcentage du Rayon
label : abs
unités : %
-
label : abs1
-
titre : Temps
label : temps
unités : secondes
-
titre : Logarithme du flux
label : flux
-
label : compteur
-
label : tim



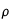 est le rapport entre la masse du corps et son volume. Son unité est le kg.m-3.
est le rapport entre la masse du corps et son volume. Son unité est le kg.m-3.
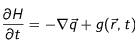
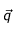 représente le flux de chaleur et
représente le flux de chaleur et 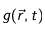 est un terme source.
est un terme source. 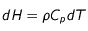 et
et 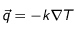
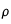 est la
est la 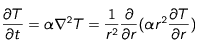 (1)
(1)
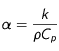 .
.
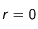 . Il faut donc définir une condition limite au centre. Ici, on impose
. Il faut donc définir une condition limite au centre. Ici, on impose 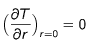 .
. 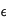 . On intègre l'équation
. On intègre l'équation 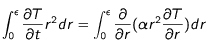 (2)
(2)
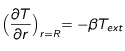 (3)
(3)
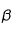 est le coefficient de convection à sa surface.
est le coefficient de convection à sa surface.
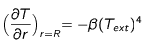 (a)
(a)
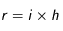 et
et 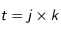 . Pour simplifier les calculs, on dédimensionne le problème de telle sorte que le rayon r varie entre 0 et 1 et
. Pour simplifier les calculs, on dédimensionne le problème de telle sorte que le rayon r varie entre 0 et 1 et 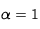 .
.

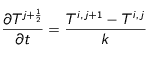 (4)
(4)
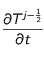 et avec les dérivées spatiales. La dérivée spatiale seconde au point
et avec les dérivées spatiales. La dérivée spatiale seconde au point 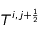 est la moyenne des dérivées spatiales secondes en j et en j+1.
est la moyenne des dérivées spatiales secondes en j et en j+1.
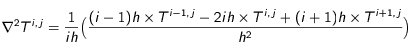 .
. 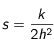 :
: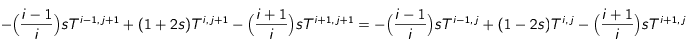 (5)
(5)
 , si
, si 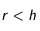 ,
, 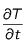 varie peu et on peut écrire :
varie peu et on peut écrire : 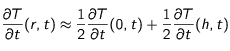 (6)
(6)
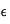 par
par 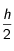 , on a :
, on a : ![\Bigl [\Bigl(\frac{\partial T}{\partial t}\Bigl)_{r=0} +\Bigl(\frac{\partial T}{\part! ial t}\Bigl)_{r=h}\Bigl]\frac{h}{12}=\frac{1}{h}(T_1-T_0)](eq_tex_profilT_doc/equation32.png) (7)
(7)
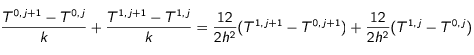 (8)
(8)
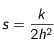 , on a finalement :
, on a finalement : 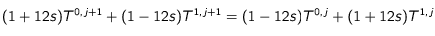 (9)
(9)
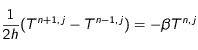
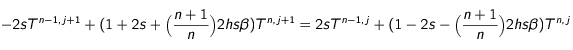 (10). En utilisant les équations
(10). En utilisant les équations 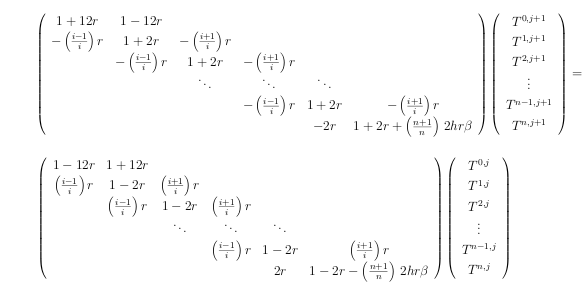
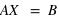
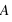 en un produit de deux matrices, l'une triangulaire inférieure
en un produit de deux matrices, l'une triangulaire inférieure 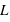 et l'autre en une matrice triangulaire supérieure
et l'autre en une matrice triangulaire supérieure 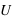 .
.
 On a donc:
On a donc:

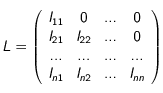 et
et 
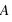 avec:
avec:
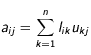
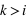
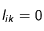 et si
et si 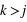
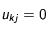 donc on se ramène à:
donc on se ramène à:
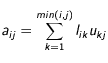
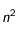 équations pour déterminer les
équations pour déterminer les 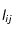 et
et 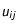 .
.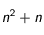 inconnues. Pour déterminer alors les coefficients, on pose tous les éléments diagonaux de
inconnues. Pour déterminer alors les coefficients, on pose tous les éléments diagonaux de 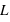 égaux à 1.
égaux à 1.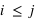 :
: 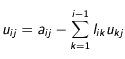
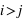 :
: 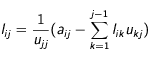
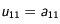 et de retrouver toutes les valeurs par
et de retrouver toutes les valeurs par 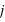 croissants pour un
croissants pour un 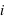 donné.
donné.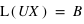
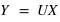 , on trouve alors:
, on trouve alors:
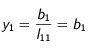
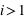 :
: 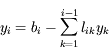
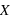 avec
avec 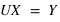 de la même façon:
de la même façon:
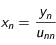
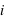 :
:
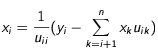
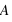 est tridiagonale donc on l'écrit:
est tridiagonale donc on l'écrit:
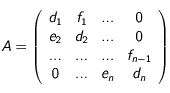
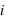 croissants:
croissants: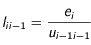
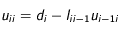
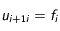 et avec
et avec 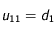
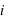 croissants:
croissants: 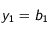
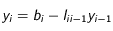
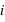 décroissants par la suite:
décroissants par la suite: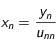
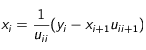
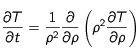 On fait donc l'hypothèse de la séparation des variables, d'où:
On fait donc l'hypothèse de la séparation des variables, d'où:
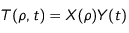 En insérant ce résultat dans l'équation de la chaleur, on obtient une équation de cette forme pour la fonction radiale:
En insérant ce résultat dans l'équation de la chaleur, on obtient une équation de cette forme pour la fonction radiale:
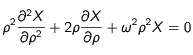 le oméga provenant d'une constante que l'on retrouve en développant les équations et qui est arbitraire.
En posant
le oméga provenant d'une constante que l'on retrouve en développant les équations et qui est arbitraire.
En posant
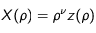 on obtient l'équation suivante:
on obtient l'équation suivante:
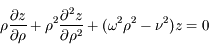 si on impose
si on impose 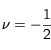 on retrouve cette forme pour les équations.
Les solutions
on retrouve cette forme pour les équations.
Les solutions 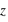 sont les fonctions de Bessel donc
sont les fonctions de Bessel donc 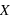 peut s'écrire:
peut s'écrire:
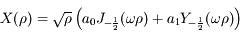 Les conditions aux limites de gradient de la température nul au centre et de variation de la température au bord proportionnelle (avec
Les conditions aux limites de gradient de la température nul au centre et de variation de la température au bord proportionnelle (avec 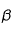 )à une température extérieure (voir cas précédent), impose comme condition pour le paramètre
)à une température extérieure (voir cas précédent), impose comme condition pour le paramètre 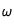 :
:
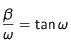 qui possède plusieurs solutions.
Dans le programme, ces valeurs sont déterminées par la méthode de Newton jusqu'à un certain ordre car la fonction tangente est périodique et donc l'équation possède plusieurs solutions. Par cette méthode on recherche les zéros de la fonction correspondante à la différence des deux membres.
On voit donc que la température est une somme de l'ensemble des solutions précédente avec la valeur de
qui possède plusieurs solutions.
Dans le programme, ces valeurs sont déterminées par la méthode de Newton jusqu'à un certain ordre car la fonction tangente est périodique et donc l'équation possède plusieurs solutions. Par cette méthode on recherche les zéros de la fonction correspondante à la différence des deux membres.
On voit donc que la température est une somme de l'ensemble des solutions précédente avec la valeur de 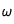 calculée par la méthode de Newton correspondante et en faisant le même travail pour la partie temporelle de la séparation des variables, on obtient finalement pour la température:
calculée par la méthode de Newton correspondante et en faisant le même travail pour la partie temporelle de la séparation des variables, on obtient finalement pour la température:
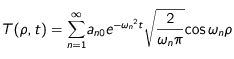 En imposant les conditions initiales pour la température égale à 1 pour tout
En imposant les conditions initiales pour la température égale à 1 pour tout 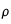 à t=0, on se retrouve avec un système linéaire à résoudre pour déterminer les coefficients
à t=0, on se retrouve avec un système linéaire à résoudre pour déterminer les coefficients 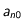 quand on tronque le développement à un certain ordre N. L'inversion de ce système par la méthode de la décomposition LU et de l'inversion qui en suit décrite plus haut permet de déterminer ces coefficients.
Une fois tous les paramètres obtenus, il suffit de calculer la valeur de la température en chaque point et à un instant t dans le programmme par la formule précédente de la température théorique obtenue et de l'afficher à l'écran.
Dans le cas théorique, le paramètre du flux
quand on tronque le développement à un certain ordre N. L'inversion de ce système par la méthode de la décomposition LU et de l'inversion qui en suit décrite plus haut permet de déterminer ces coefficients.
Une fois tous les paramètres obtenus, il suffit de calculer la valeur de la température en chaque point et à un instant t dans le programmme par la formule précédente de la température théorique obtenue et de l'afficher à l'écran.
Dans le cas théorique, le paramètre du flux 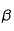 est limité à certaines valeurs car la sommation effectuée dans le programme est réalisée des valeurs les plus faibles supposée des coefficients aux plus grands et quand ce paramètre est trop grand les calculs sont faussés.
La courbe théorique sur le graphe est tracée en rouge et est proche du calcul numérique à certains moments et éloignée à d'autres, car notre hypothèse de séparation des variables n'est qu'une approximation résultante d'une constatation faite à partir du profil calculé par notre programme.
est limité à certaines valeurs car la sommation effectuée dans le programme est réalisée des valeurs les plus faibles supposée des coefficients aux plus grands et quand ce paramètre est trop grand les calculs sont faussés.
La courbe théorique sur le graphe est tracée en rouge et est proche du calcul numérique à certains moments et éloignée à d'autres, car notre hypothèse de séparation des variables n'est qu'une approximation résultante d'une constatation faite à partir du profil calculé par notre programme.
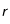 (coordonnées sphériques) par rapport au centre de l'astre.
(coordonnées sphériques) par rapport au centre de l'astre.
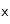 positifs (
positifs (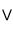 . Appliquons le modèle du "
. Appliquons le modèle du " 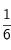 '' (c'est-à-dire, considérons que les particules se déplacent toutes selon les axes). Dans ce cas, le flux de particules à travers la section
'' (c'est-à-dire, considérons que les particules se déplacent toutes selon les axes). Dans ce cas, le flux de particules à travers la section
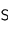 pendant
pendant 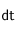 vaut :
vaut :
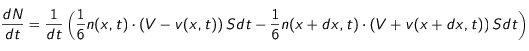
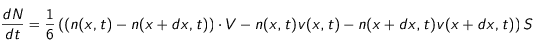
 est le nombre élémentaire de particules traversant
est le nombre élémentaire de particules traversant 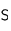 pendant l'intervalle de temps
pendant l'intervalle de temps 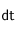 ,
, 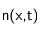 est la densité de particules en
est la densité de particules en 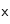 à l'instant
à l'instant 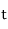 , et
, et 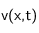 la vitesse des particules sédimentant.
la vitesse des particules sédimentant.
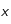 et
et 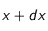 (autrement dit
(autrement dit 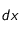 ) est de l'ordre du libre parcours moyen
) est de l'ordre du libre parcours moyen 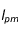 des particules, alors le flux de particules
des particules, alors le flux de particules 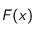 par unité de temps à travers la surface
par unité de temps à travers la surface 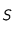 sera :
sera : 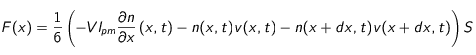
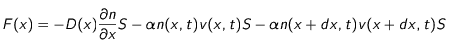
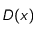 est le coefficient de diffusion des particules et peut dépendre de la position
est le coefficient de diffusion des particules et peut dépendre de la position 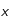 , et
, et 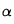 un coefficient que l'on peut assimiler au pourcentage de particules qui vont effectivement sédimenter dans la direction
un coefficient que l'on peut assimiler au pourcentage de particules qui vont effectivement sédimenter dans la direction 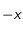 avec la vitesse
avec la vitesse 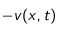 (en supposant, pour simplifier, que
(en supposant, pour simplifier, que 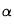 ne dépend ni de la position, ni du temps).
ne dépend ni de la position, ni du temps).
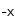 est le même en
est le même en 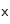 et
et 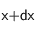 , alors l'expression du flux devient :
, alors l'expression du flux devient : 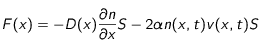
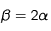 sans dimension) :
sans dimension) : 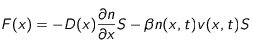 (11)
(11)
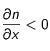 et donc
et donc 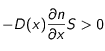 lorsque les densités élevées sont au centre)
lorsque les densités élevées sont au centre)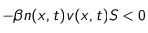 pour
pour 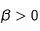 )
)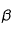 , à obtenir soit de la sédimentation si
, à obtenir soit de la sédimentation si 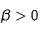 , soit un phénomène de pseudodiffusion si
, soit un phénomène de pseudodiffusion si 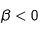 ).
).

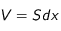
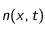 . Le nombre élémentaire de particules traversant une surface
. Le nombre élémentaire de particules traversant une surface 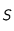 pendant un intervalle de temps
pendant un intervalle de temps 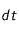 est :
est :

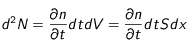 (12)
(12)
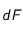 entre
entre 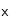 et
et 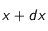 est :
est : ![dF=F(x+dx)-F(x)={\frac{\partial F}{\partial x}}dx={\frac{\partial}{\partial x}\left[-D(x){\frac{\partial n}{\partial x}}-{\beta}n(x,t)v(x,t)\right]}Sdx](eq_tex_profilT_doc/equation133.png)
![dF=-\left[{\frac{\partial}{\partial x}}\left(D(x){\frac{\partial n}{\partial x}}\right)+{\beta}\frac{\partial\left(nv\right)}{\partial x}\right]Sdx](eq_tex_profilT_doc/equation134.png) (13)
(13)
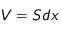 entre
entre 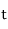 et
et 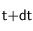 vaut :
vaut : 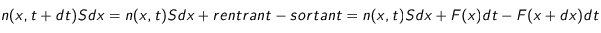
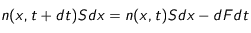 (14)
(14)
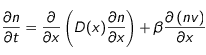
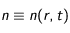 et
et 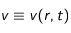 .
.

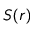 par unité de temps vaut :
par unité de temps vaut : 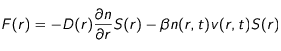
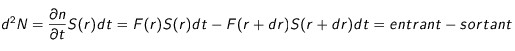
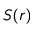 en sphérique vaut :
en sphérique vaut : 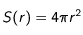 .
.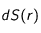 et non
et non 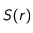 . Dans le cas général,
. Dans le cas général, 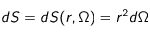 .
Cependant, en considérant un cas isotrope, aucune grandeur ne dépend de l'angle solide, et par conséquent, on peut intégrer sur tout l'angle
solide, ce qui revient à n'intégrer que
.
Cependant, en considérant un cas isotrope, aucune grandeur ne dépend de l'angle solide, et par conséquent, on peut intégrer sur tout l'angle
solide, ce qui revient à n'intégrer que 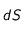 selon
selon 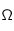 ce qui donne
ce qui donne 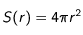 .
.
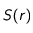 par son expression puis simplifié par
par son expression puis simplifié par  , on obtient :
, on obtient :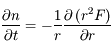
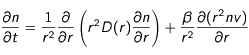 (15)
(15)
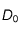 et
et 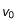 , grandeurs dimensionnées caractéristiques du coefficient de diffusion
, grandeurs dimensionnées caractéristiques du coefficient de diffusion 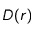 et de la vitesse de sédimentation des particules
et de la vitesse de sédimentation des particules 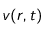 , telles que
, telles que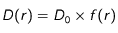
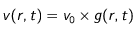
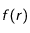 et
et 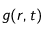 sont sans dimension.
sont sans dimension.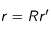
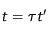
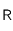 et
et 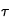 sont des grandeurs caractéristiques du problème (ici,
sont des grandeurs caractéristiques du problème (ici, 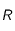 correspondrait au rayon de la source, et
correspondrait au rayon de la source, et 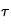 au temps caractéristique d'évolution de la densité). L'équation
au temps caractéristique d'évolution de la densité). L'équation 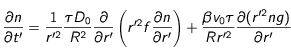
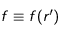 et
et 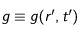 .
.
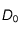 ,
, 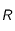 , et
, et 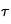 telles que
telles que 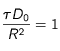 . Posons
. Posons 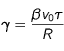 (notons que, comme
(notons que, comme 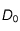 est en
est en 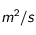 et que
et que 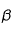 est sans dimension, l'homogénéïté pour les deux égalités est bien respectée).
L'équation adimensionnée est donc :
est sans dimension, l'homogénéïté pour les deux égalités est bien respectée).
L'équation adimensionnée est donc :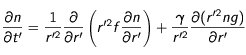 (16)
(16)
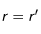 dans les équations
(
dans les équations
(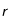 sans dimension).
sans dimension).
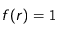 et
et 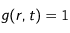 , de sorte que l'équation
, de sorte que l'équation 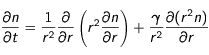 (17)
(17)
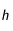 et un pas temporel
et un pas temporel 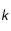 . Ensuite, il va s'agir d'établir l'expression discrétisée de l'équation précédente en
. Ensuite, il va s'agir d'établir l'expression discrétisée de l'équation précédente en 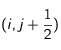 (indice spatial, indice temporel),
(indice spatial, indice temporel), 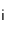 et
et 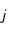 étant des entiers.
On a alors :
étant des entiers.
On a alors : 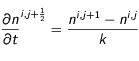 (18)
(18)
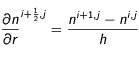
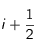 (respectivement
(respectivement 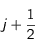 ) apparaît pour une variable, étant donné que l'on a discrétisé en nombres entiers de
) apparaît pour une variable, étant donné que l'on a discrétisé en nombres entiers de 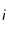 et de
et de 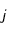 , alors on calculera la valeur en ce point comme étant la valeur moyenne du point suivant
, alors on calculera la valeur en ce point comme étant la valeur moyenne du point suivant 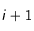 (respectivement
(respectivement 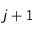 ) et du point précédent
) et du point précédent 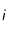 (respectivement
(respectivement 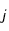 ).
).
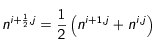
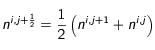

 de même pour toute dérivée partielle d'ordre
de même pour toute dérivée partielle d'ordre 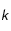 par rapport à une variable
par rapport à une variable 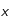 , on aura :
, on aura :
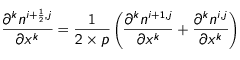
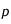 est le pas relatif à la variable
est le pas relatif à la variable 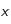 (dans notre cas,
(dans notre cas, 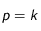 si
si 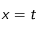 , ou
, ou 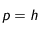 si
si 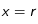 .
.
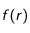 qui est :
qui est : 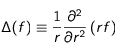
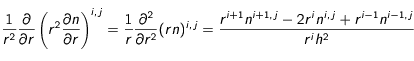
 Il s'ensuit que le laplacien de
Il s'ensuit que le laplacien de 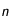 pris en
pris en 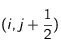 s'écrit :
s'écrit :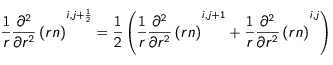
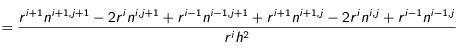 (19)
(19)

 De même, on trouve que :
De même, on trouve que :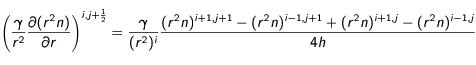 (20)
(20)
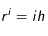 et
et 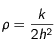 .
.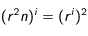 ainsi, on voit facilement que
ainsi, on voit facilement que 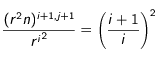
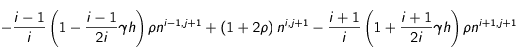
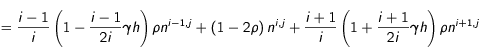 (21)
(21)
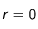 :
: 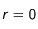 , nous allons procéder de la même façon que dans la cas sans source, c'est-à-dire en intégrant l'équation
, nous allons procéder de la même façon que dans la cas sans source, c'est-à-dire en intégrant l'équation
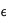 . Nous considèrerons qu'en
. Nous considèrerons qu'en 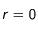 , le gradient de densité est nul pour n'importe quel temps
, le gradient de densité est nul pour n'importe quel temps 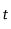 donc quelque soit
donc quelque soit 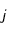 (
(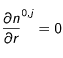 ).
).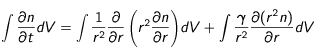
 , ce qui donne, lorsque l'on considère un problème à symétrie sphérique (après simplification par
, ce qui donne, lorsque l'on considère un problème à symétrie sphérique (après simplification par 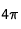 ):
):
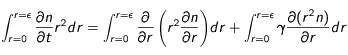 (22)
(22)
 par
par  ) est la présence d'un second terme à intégrer dans le membre de droite de l'équation ci-dessus. Nous allons donc ne nous occuper que de l'intégration de ce terme et de son écriture via Crank-Nicholson, l'intégration des deux autres termes ayant déjà été faite dans la cas de l'équation de la chaleur avec diffusion seule.
) est la présence d'un second terme à intégrer dans le membre de droite de l'équation ci-dessus. Nous allons donc ne nous occuper que de l'intégration de ce terme et de son écriture via Crank-Nicholson, l'intégration des deux autres termes ayant déjà été faite dans la cas de l'équation de la chaleur avec diffusion seule.![\int_{0}^{\epsilon} {\gamma \frac{\partial (r^2n)}{\partial r}}dr=\gamma \int_{0}^{\epsilon} {\partial (r^2n)}=\gamma {\left[r^2n\right]}_{0}^{\epsilon}=\gamma \epsilon ^2 n(\epsilon,t)](eq_tex_profilT_doc/equation247.png) (23)
(23)
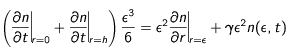
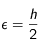 (milieu de la première maille, on obtient après une petite séance de gymnastique mathématique, la condition au centre :
(milieu de la première maille, on obtient après une petite séance de gymnastique mathématique, la condition au centre : 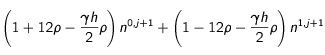
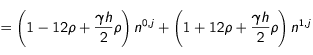 (24)
(24)
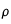 vaut toujours
vaut toujours 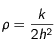 ).
).
 :
: 
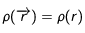 et donc en intégrant sur les deux angles
et donc en intégrant sur les deux angles  et
et  :
: 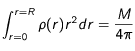 ou encore, avec le changement de variable
ou encore, avec le changement de variable 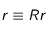 :
: 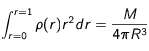
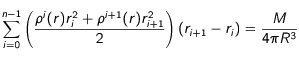
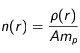 , où
, où 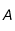 correspond au nombre de nucléons de l'élément radioactif et
correspond au nombre de nucléons de l'élément radioactif et 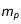 à la masse d'un proton ; rappelons que
à la masse d'un proton ; rappelons que 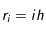 ) donnant une condition en
) donnant une condition en 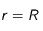 :
: 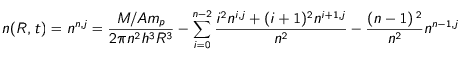 (23)
(23)
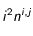 et en
et en 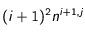 se ressemblent, reprenons-les et essayons d'arranger la somme différemment :
se ressemblent, reprenons-les et essayons d'arranger la somme différemment :
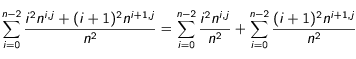
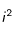 et appliquons-lui le changement de variable suivant :
et appliquons-lui le changement de variable suivant : 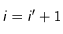 . Ce terme se réécrit donc :
. Ce terme se réécrit donc :
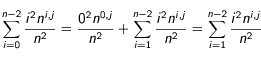
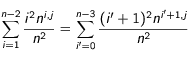
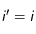 :
:
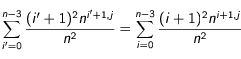
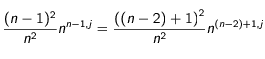
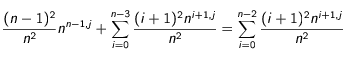
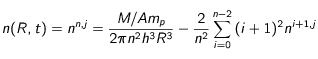
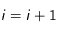 ) :
) : 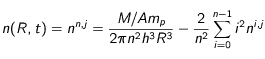
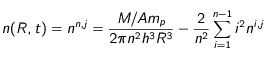 (25)
(25)
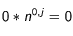 .
.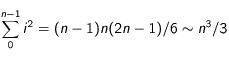 ,
, 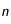 suffisament grand) :
suffisament grand) :
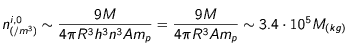
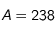 ) avec
) avec 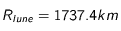 ,
,  étant la masse totale d'uranium à l'intérieur de la Lune que
l'utilisateur pourra choisir.
étant la masse totale d'uranium à l'intérieur de la Lune que
l'utilisateur pourra choisir.
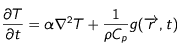
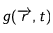 est le terme source. Rappelons que
est le terme source. Rappelons que 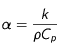 est la diffusivité thermique.
est la diffusivité thermique.
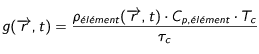
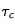 correspondrait au temps caractéristique nécessaire pour qu'un élément radioactif à la température
correspondrait au temps caractéristique nécessaire pour qu'un élément radioactif à la température 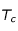 présent dans un volume
présent dans un volume 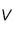 avec une densité
avec une densité 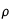 transfère une densité d'énergie
transfère une densité d'énergie 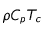 au milieu qui l'entoure. On sait que
au milieu qui l'entoure. On sait que 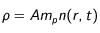 où
où 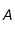 représente le nombre de nucléons de l'élément radioactif (en effet, puisque
représente le nombre de nucléons de l'élément radioactif (en effet, puisque 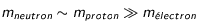 , on peut assimiler la masse atomique de l'élément à
, on peut assimiler la masse atomique de l'élément à 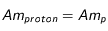 ). Par ailleurs, compte-tenu du fait que le volume considéré est celui de la Lune et que l'on a fait l'hypothèse d'un problème à symétrie sphérique, on peut alors réécrire le terme source sous la forme suivante :
). Par ailleurs, compte-tenu du fait que le volume considéré est celui de la Lune et que l'on a fait l'hypothèse d'un problème à symétrie sphérique, on peut alors réécrire le terme source sous la forme suivante :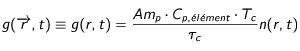
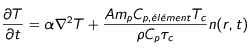
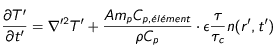 (26)
(26)
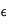 représente la "magnitude'' de
représente la "magnitude'' de 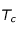 une fois dédimensionnée et est positif ;
une fois dédimensionnée et est positif ; 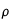 correspond à la masse volumique du milieu et donc ici à la masse volumique de la Lune (
correspond à la masse volumique du milieu et donc ici à la masse volumique de la Lune (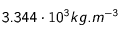 ) ;
) ; 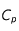 ainsi que
ainsi que 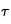 et
et 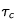 n'étant a priori pas connus, on choisira de prendre le paramètre libre
n'étant a priori pas connus, on choisira de prendre le paramètre libre 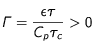 homogène à des
homogène à des 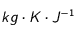 dont la valeur sera définie par l'utilisateur. En utilisant à présent les valeurs des différentes grandeurs connues (et que
dont la valeur sera définie par l'utilisateur. En utilisant à présent les valeurs des différentes grandeurs connues (et que 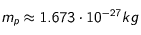 ),
), 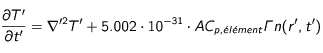 (27)
(27)
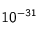 fera que le terme source ne changera absolument rien. Voici un petit calcul qui montre que cette intuition est fausse. Dans notre modélisation incluant un élément radioactif minoritaire, il
faut bien faire attention à la signification de minoritaire. Supposons que cet élément soit de l'uranium 238, minoritaire signifie que son
abondance Ab est faible par rapport à celle de l'élément prépondérant. Appelons
fera que le terme source ne changera absolument rien. Voici un petit calcul qui montre que cette intuition est fausse. Dans notre modélisation incluant un élément radioactif minoritaire, il
faut bien faire attention à la signification de minoritaire. Supposons que cet élément soit de l'uranium 238, minoritaire signifie que son
abondance Ab est faible par rapport à celle de l'élément prépondérant. Appelons  de masse
de masse 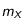 et de nombre de nucléons
et de nombre de nucléons 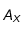 l'élément le plus abondant de la Lune, et supposons que l'abondance d'uranium 238 soit très faible :
l'élément le plus abondant de la Lune, et supposons que l'abondance d'uranium 238 soit très faible :
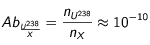
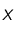 au sein de la Lune est donc :
au sein de la Lune est donc :
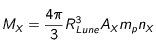
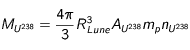
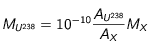
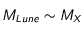 , dès lors, nous avons :
, dès lors, nous avons :
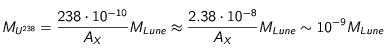
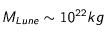 donc
donc 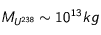 , on trouve finalement une densité d'élément radioactif :
, on trouve finalement une densité d'élément radioactif :
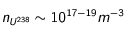
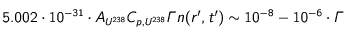
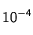 minimum ont un effet nettement visible sur la température, ce qui implique de choisir
minimum ont un effet nettement visible sur la température, ce qui implique de choisir 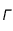 suffisamment grand (
suffisamment grand (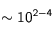 ) si l'on prend une abondance d'uranium aussi faible. On pourra donc prendre des valeurs faibles de
) si l'on prend une abondance d'uranium aussi faible. On pourra donc prendre des valeurs faibles de 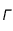 pour des masses d'uranium plus grandes, et jouer avec les valeurs de ce paramètre pour une masse
donnée.
pour des masses d'uranium plus grandes, et jouer avec les valeurs de ce paramètre pour une masse
donnée.





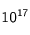 kg d'uranium 238 en "suspension" à l'intérieur de la Lune, avec un paramètre de sédimentation de 10, on observe l'évolution suivante :
kg d'uranium 238 en "suspension" à l'intérieur de la Lune, avec un paramètre de sédimentation de 10, on observe l'évolution suivante :

