Simulation: Influence de la turbulence atmosphérique sur les images
Auteur: François Lacombe (version originale), Alain Hui-Bon-Hoa (version JAVA)
Date de mise à jour: 4/7/2002
Introduction:
La traversée de l'atmosphère par la lumière des astres observés depuis le sol occasionne une forte dégradation des images obtenues.
En effet, l'atmosphère est composée de différentes masses d'air ayant chacune une température et une vitesse de déplacement propre. A l'interface entre ces masses d'air existent de forts gradients de température qui engendrent des écoulements de particules à caractère turbulent. Ces mouvements se traduisent par des fluctuations aléatoires de densité et donc d'indice de réfraction de l'air. Localement s'opèrent des avances ou retards de phase aléatoires dont l'effet global est une déformation du front d'onde. A cette déformation du front d'onde incident dans le plan de la pupille du télescope correspondra un changement des conditions d'interférences dans le plan focal et donc l'éclatement de l'image en tavelures ou speckles, lieux des seules interférences constructives.
L'appliquette est disponible en suivant ce lien.
Retour au menu des appliquettes.
Objectifs:
Le but de cette appliquette est d'expérimenter l'influence de
la turbulence atmosphérique sur l'image d'un objet ponctuel (une tache d'Airy, puisque la pupille a une taille finie).
Module: optique adaptative ; cours: formation des images
Détails sur la mise en oeuvre:
Modélisation numérique
Selon un modèle d'atmosphère dû à Kolmogorov, les fluctuations d'indices sont gouvernées par un transfert d'energie cinétique des structures turbulentes de grande taille vers celle de taille plus petite. D'apres ce modèle, et sous réserve que certaines hypothèses d'isotropie, de stationnarité, etc, soient respectées, la densité spectrale de la phase du front d'onde au niveau de la pupille du télescope suit alors statistiquement une loi de puissance en 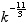 , où k est la fréquence spatiale.
, où k est la fréquence spatiale.
Mathématiquement, la phase du front d'onde sur une pupille circulaire peut être décomposée sur une base orthonormée de polynômes, dits de Zernike, caractérisés par un nombre radial n et un nombre azimutal m.
Une manière de construire un front d'onde turbulent est de superposer une série de polynômes de Zernike, où la variance temporelle de chaque coefficient, dépendra de l'ordre radial du polynôme par une loi de puissance :
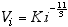
La valeur de K peut être obtenue par normalisation en utilisant la relation suivante, due à Noll :
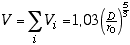
où V décrit la variance temporelle globale de l'erreur de phase dans la pupille.
V dépend ainsi d'un paramètre scalaire, r0, homogène à une longueur, qui représente par ailleurs l'étendue de cohérence du front d'onde dans la pupille. Le facteur sans dimension D/r0, rapport du diamètre du télescope à l'étendue de cohérence du front d'onde, caractérise la cohérence de la pupille et ainsi la force de la turbulence.
Remarque:
la faible dépendance chromatique de l'indice de réfraction de l'air permet de d'affirmer, en première approximation, que l'erreur de phase est directement proportionnelle à l'inverse de la longueur d'onde (et la variance V a son carré). On voit ainsi que r0 depend de la longueur d'onde selon une loi de puissance en (6/5).
Application
Pour simuler un front d'onde turbulent, comme dans cette appliquette, on choisit d'abord le nombre maximal Nz de polynômes de Zernike sur lesquels la décomposition (et la reconstruction) de la phase sera effectuée. Plus il est grand, plus la simulation est réaliste, mais plus le temps de calcul est important...
On choisit ensuite le facteur D/r0. Une valeur typique pour un télescope de 8m dans le proche IR est de 30. Elle monte à 80, voire plus, dans le visible.
On tire alors au hasard Nz valeurs normalement distribuées autour de 0 avec un écart-type de 1. On pondère ces Nz coefficients par une loi de puissance en 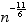 , normalisés de telle sorte que la somme de leurs carrés soit bien égale à
, normalisés de telle sorte que la somme de leurs carrés soit bien égale à 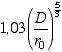 .
.
Attention :
- par convention, le Zernike de rang 1 est le piston, sans effet ici. Nos Nz polynômes sont en réalité les polynômes de rang 2 a Nz+1
- n est le numéro d'ordre radial d'un Zernike de rang i+1 (1 < i < Nz), et non le rang lui-même. Ce dernier correspond à un rangement linéaire par ordre radial croissant, puis par ordre azimutal croissant.
- en terme d'écart-type, la loi en -11/3 devient bien sûr -11/6.
L'ensemble est alors bien une fonction de phase qui satisfait (au nombre fini de polynômes près) a une statistique de Kolmogorov. Associée a une fonction d'amplitude unité, cette phase permet alors de construire la fonction pupille complexe instantanée dont le carré de la transformée de Fourier est l'image instantanée.
L'appliquette permet de fixer la quantité D/r0, bien sûr, mais aussi d'activer ou non certains polynômes pour en voir les effets sur l'image, sans modifier les autres.
Liste des paramètres de l'appliquette:
-
label: doverR
type: nombre
titre: D/r0
unités: sans unité
mode d'acquisition: champ
Rapport du diamètre D de la pupille à son étendue de cohérence r0 (paramètre de Fried)
-
label: nb_zernike
type: nombre
titre: Nombre de polynômes de Zernike cumulés
unités:
mode d'acquisition: champ
Nombre maximal de polynômes de Zernike pris en compte
-
label: z2
type: string
titre: Zernike ordre 2 (tip)
unités:
mode d'acquisition: case
A cocher pour activer le polynôme de Zernike d'ordre 2 ("tip")
-
label: z3
type: string
titre: Zernike ordre 3 (tilt)
unités:
mode d'acquisition: case
A cocher pour activer le polynôme de Zernike d'ordre 3 ("tilt")
-
label: z4
type: string
titre: Zernike ordre 4 (focus)
unités:
mode d'acquisition: case
A cocher pour activer le polynôme de Zernike d'ordre 4 ("défocalisation")
-
label: z5
type: string
titre: Zernike ordre 5 (Astigmatisme 0°)
unités:
mode d'acquisition: case
A cocher pour activer le polynôme de Zernike d'ordre 5 ("astigmatisme 0°")
-
label: z6
type: string
titre: Zernike ordre 6 (Astigmatisme 45°)
unités:
mode d'acquisition: case
A cocher pour activer le polynôme de Zernike d'ordre 6 ("astigmatisme 45°")
-
label: z7etPlus
type: string
titre: Zernike ordres 7 et + (Comas et suivants)
unités:
mode d'acquisition: case
A cocher pour activer le polynôme de Zernike d'ordre 7 et supérieurs ("comas" etc.)
Mode d'emploi de l'appliquette:
Au lancement de l'appliquette, une fenêtre apparaît comme ci-dessous.
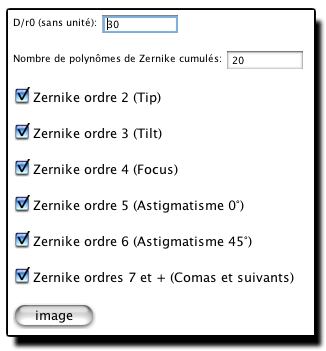
Une fois le calcul demandé, la fenêtre prend l'aspect illustré ci-dessous.
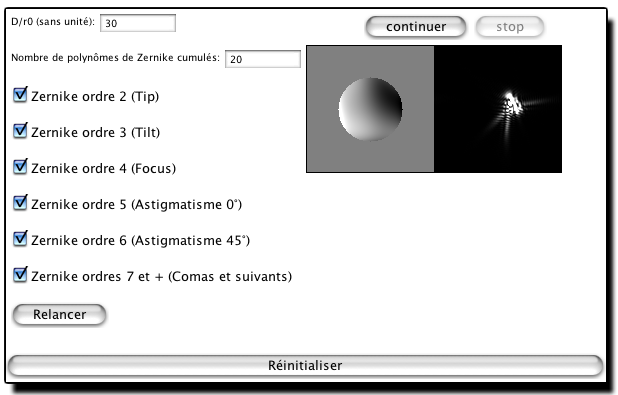
Le bouton "stop" permet de suspendre le calcul. Quand on clique dessus l'animation s'arrête, le bouton "stop" devient grisé et le bouton "continuer" peut être activé afin de poursuivre l'expérience.
Une action sur le bouton "Relancer" provoque le lancement d'un nouveau calcul, avec les nouvelles valeurs des paramètres s'il y a lieu.
Tout en bas, le bouton "Réinitialiser" ramène au premier écran.
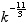 , où k est la fréquence spatiale.
, où k est la fréquence spatiale.
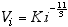
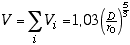
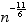 , normalisés de telle sorte que la somme de leurs carrés soit bien égale à
, normalisés de telle sorte que la somme de leurs carrés soit bien égale à 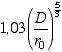 .
.

