Le problème à trois corps restreint
Auteur: Aurélie Guilbert
Auteur: Benoît Carry
Auteur: Nicolas Delsate
Date de création : 06/01/06
Introduction
Cette applet permet la simulation du problème à trois corps plan restreint. On s'intéresse alors au mouvement d'une particule test dans le champ de gravité créé par deux masses.
Rappels de cours
Le but de l'applet est de tracer la trajectoire d'une particule test dans le champ de gravité de deux masses, dont le mouvement relatif est supposé circulaire uniforme. On suppose également que la particule test ne perturbe pas les deux masses principales, et que son mouvement se fait dans le même plan que le mouvement de ces deux masses, sous la seule influence de la gravitation.
Les équations du mouvement de la particule test seront dérivées du formalisme hamiltonien, plus adapté aux problèmes de mécanique céleste.
Les deux corps principaux, de masses respectives
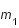
et
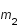
, sont en mouvement dans le plan
Oxy, séparés par une distance
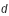
. On suppose que
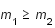
. Le mouvement de ces deux corps est circulaire uniforme, de vitesse angulaire
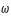
constante. La masse de la particule test est
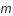
, et la particule est située en
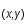
.
La formulation de ces équations dans ce formalisme conduit à l'introduction de divers paramètres :
-
Lagrangien
:
Il faut dans un premier temps établir l'équation du Lagrangien. L'énergie cinétique de la particule est :
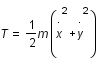 .
.
Son énergie potentielle est :
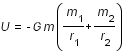
avec :
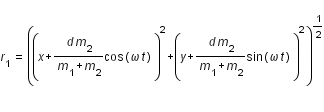
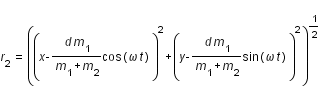 .
.
Le Lagrangien est alors :
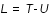 .
.
Les diverses expressions sont lourdes, et vont être simplifiées en choisissant des unités plus adaptées.
-
D
édimensionnement
:
Il est nécessaire pour dériver les équations du mouvement de réduire le nombre de paramètres et d'utiliser des variables plus adaptées. On va alors poser :
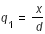 ,
, 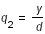 ,
, 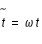 ,
, 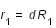 ,
, 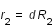 .
.
On va aussi introduire le paramètre de masse : 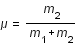 , compris entre 0 et 0.5. On arrive alors à une expression plus simple pour le Lagrangien, qui devient :
, compris entre 0 et 0.5. On arrive alors à une expression plus simple pour le Lagrangien, qui devient :
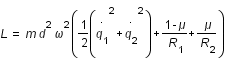 .
.
Les équations de Lagrange étant invariantes par multiplication par une constante, on peut considérer que le Lagrangien est :
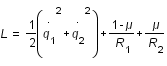 .
.
-
Hamiltonien
Les moments conjugués de (q
1
, q
2
) sont : 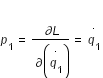 et
et 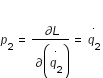 . L'hamiltonien s'écrit alors :
. L'hamiltonien s'écrit alors :
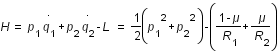 .
.
Il se trouve que cet hamiltonien dépend du temps par l'intermédiaire de R
1 et R
2. Pour éliminer cette dépendance explicite en temps, on se place dans le référentiel tournant, ce qui permet de s'affranchir du mouvement des deux corps principaux. Cette opération permet d'écrire un nouvel hamiltonien (les nouvelles coordonnées généralisées sont calculées dans le repère tournant) :
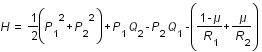
avec :
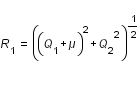
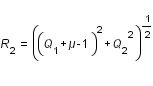 .
.
Pour plus d'informations sur les méthodes numériques, le calcul de la trajectoire ou le calcul des points de Lagrange.
Liste des paramètres de l'applet
-
type : nombre
titre : mu
Mu est le paramètre de masse défini précedemment.
-
type : nombre
titre : pas d'intégration
Le pas d'intégration permet de définir le temps demandé entre deux itérations du calcul de la trajectoire. Plus il est petit, plus la trajectoie sera bien échantillonnée. Mais attention, un pas trop petit engendre un temps de calcul plus long.
-
type : nombre
titre : Ralentissement
Le ralentissement est un nombre entier qui correspond au nombre de millisecondes qu'on demande entre l'affichage de deux points successifs. En effet, le calcul peut être très rapide et donc être affiché très rapidement aussi, sans que l'utilisateur ne puisse voir les détails du tracé.
-
type : nombre
titre : q1
q1 est la première coordonnée généralisée, relative à x dans le plan Oxy.
-
type : nombre
titre : q2
q2 est la première coordonnée généralisée, relative à y dans le plan Oxy.
-
type : nombre
titre : q1point
q1point est la dérivée par rapport au temps de la première coordonnée généralisée.
-
type : nombre
titre : q2point
q2point est la dérivée par rapport au temps de la première coordonnée généralisée.
-
type : nombre
titre : ajustement
La question est de savoir si l'utilisateur veut que les fenêtres graphiques soient ajustées automatiquement ou non. Si oui, cocher cette case, et ne pas oublier de la cocher à chaque initialisation.
-
type : nombre
titre : courbe de vitesse nulle
La question est de savoir si l'utilisateur veut voir ou non les courbes de vitesse nulle. Si oui, alors il faut cocher cette case, et demander le calcul des courbes de vitesses nulles, pas un autre. Sinon, ne pas la cocher, et demander un autre calcul.
Mode d'emploi de l'applet
Au lancement de l'applet, une fenêtre apparait comme ci-dessous :
lancement
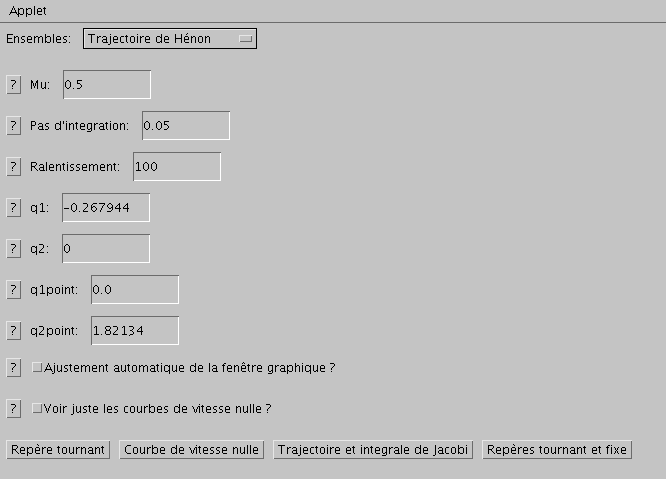
Fenêtre qui aparaît au lancement de l'applet.
Crédit :
Aurélie Guilbert, Benoit Carry, Nicolas Delsate.
L'utilisateur a alors le choix entre :
- Remplir les différents champs lui-même,
- Sélectionner une série de paramètres pré-enregistrés dans la liste. Ces paramètres correspondent à des trajectoires intéressantes pour leur forme...
Il convient ensuite de choisir si l'ajustement de la fenêtre graphique doit se faire automatiquement ou non. Si oui, cocher la case.
Remarque :
Il ne faut pas oublier de cocher la case à chaque réinitialisation.
L'utilisateur doit choisir s'il souhaite voir les courbes de vitesse nulle ou pas. Si oui, il convient de cocher la case correspondante, et de cliquer sur le bouton qui deande le calcul des courbes de vitesse nulle. Si non, ne pas cocher cette case, et choisir un autre calcul.
vitessenulle
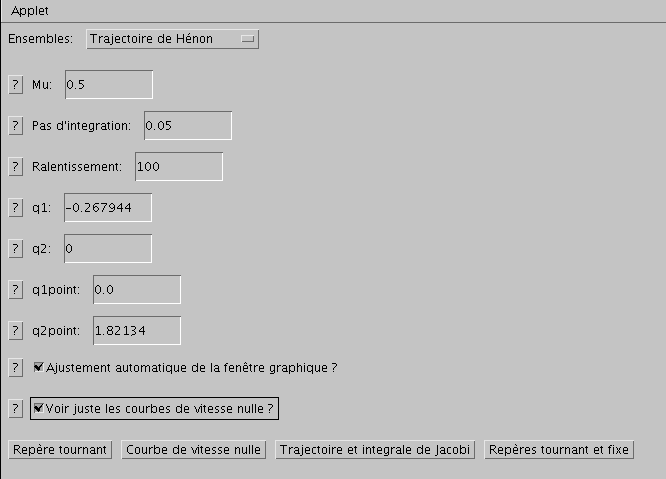
Pour voir les courbes de vitesse nulle, il faut cocher la case correspondante, et demander le calcul des courbes de vitesse nulle. il est préférable de cocher aussi la case qui demande l'ajustement automatique des fenêtres graphiques.
Crédit :
Aurélie Guilbert, Benoit Carry, Nicolas Delsate.
Divers types de calculs sont alors envisageables : trajectoire dans le repère tournant, dans le repère tournant et fixe, avec intégrale de Jacobi... Cliquer sur le bouton correspondant au calcul souhaité.
Une fois la calcul demandé, la fenêtre prend l'aspect suivant:
calculdemandé
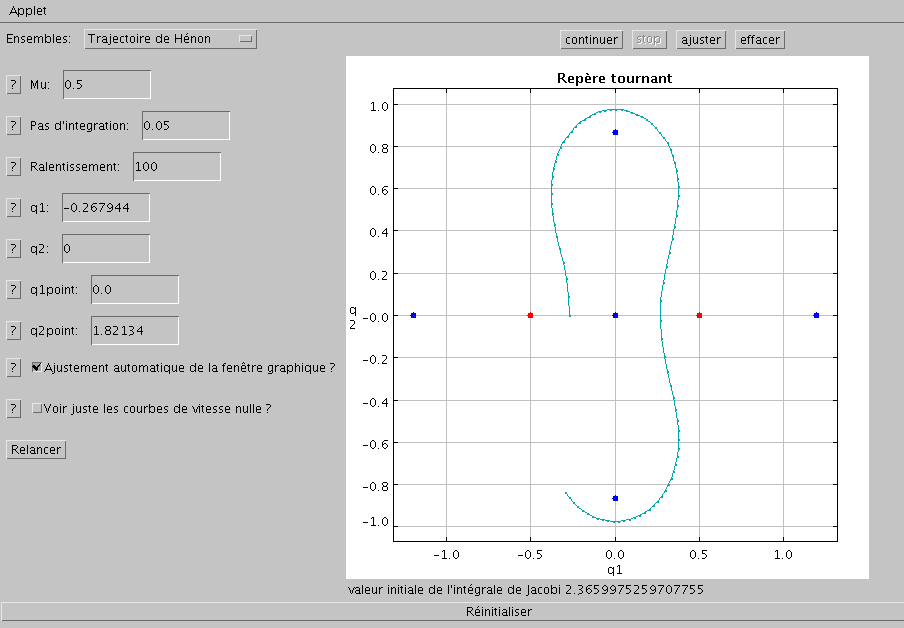
Fenêtre qui aparaît lorsque le calcul est lancé. Ici, la trajectoire de Hénon est tracée, et l'ajustement de la fenêtre graphique a été demandé.
Crédit :
Aurélie Guilbert, Benoit Carry, Nicolas Delsate.
Le bouton "stop" permet de stopper le calcul a tout moment.
Remarque :
Si la trajectoire montre que la particule est éjectée du système, il est préférable de stopper le calcul !
Le bouton "effacer" permet d'effacer tout ce qui a été affiché dans la fenêtre graphique.
Le bouton "ajuster" permet d'ajuster la fenêtre graphique à tout moment. Il est inutile lorsque l'ajustement automatique a été demandé.
Remarque :
Lorsque l'ajustement automatique n'est pas demandé, il est possible de zoomer sur une partie du graphique en la sélectionnant avec la souris.
Le bouton "relancer" permet de relancer le calcul. Il est alors préférable d'avoir effacé la fenêtre graphique. Cependant, il est aussi possible de superposer plusieurs trajectoires grâce à ce bouton, sous certaines conditions bien sûr : on peut ainsi superposer les courbes "fer à cheval".
Le barre "réinitialiser" permet de revenir à la fenêtre précédente afin de donner de nouvelles conditions initiales.
A tout moment, lorsque le calcul est stoppé, l'utilisateur peut changer les conditions inscrites dans les différents champs, et relancer le calul avec ces nouvelles conditions. Il est alors préférable d'avoir au préalable effacé l'écran.
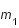 et
et 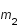 , sont en mouvement dans le plan Oxy, séparés par une distance
, sont en mouvement dans le plan Oxy, séparés par une distance 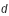 . On suppose que
. On suppose que 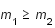 . Le mouvement de ces deux corps est circulaire uniforme, de vitesse angulaire
. Le mouvement de ces deux corps est circulaire uniforme, de vitesse angulaire 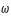 constante. La masse de la particule test est
constante. La masse de la particule test est 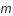 , et la particule est située en
, et la particule est située en 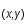 .
.
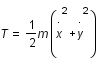 .
.
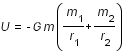
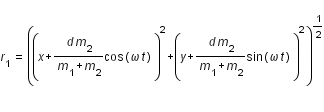
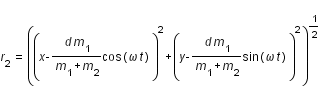 .
.
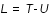 .
.
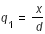 ,
, 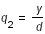 ,
, 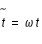 ,
, 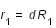 ,
, 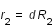 .
.
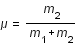 , compris entre 0 et 0.5. On arrive alors à une expression plus simple pour le Lagrangien, qui devient :
, compris entre 0 et 0.5. On arrive alors à une expression plus simple pour le Lagrangien, qui devient :
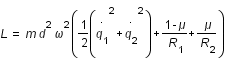 .
.
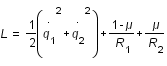 .
.
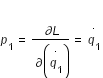 et
et 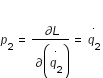 . L'hamiltonien s'écrit alors :
. L'hamiltonien s'écrit alors :
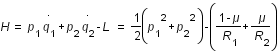 .
.
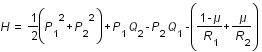
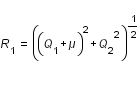
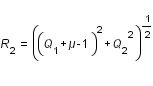 .
.


