|
Image du disque autour d'un trou noir
Auteur: COUETDIC Jocelyn
Auteur: DUMAS Gaëlle
Auteur: FERRAND Gilles
Date de création : 24/02/04
Date de mise à jour : 08/03/04
Introduction
Cette applet permet de tracer l'image d'un disque d'accrétion géométriquement fin et optiquement épais en rotation képlerienne autour d'un trou noir de Schwarzschid. On peut en fait tracer 3 images :
- l'image géométrique : iso-r
- la carte du redshift : iso-z
- la "photo" du flux (bolométrique) : iso-F
Toutes ces images sont animées : l'observateur tourne en boucle autour du trou noir (selon un axe passant pas son disque).
Rappels de cours
La physique du problème est présentée dans le cours
Images et spectre d'un disque fin autour d'un trou noir
Liste des paramètres de l'applet
-
label : rMax
type : nombre
titre : rayon maximal du disque
unités : rayon gravitationnel (Rg=M pour c=G=1)
Rentrer ici la valeur du rayon externe du disque (typiquement rMax = 100 Rg, au maximum rMax = 180 Rg de part la taille du cadre). Rq1 : le rayon minimal d'un disque d'accrétion est toujours rMin = 6 Rg. Rq2 : le temps de calcul augmente rapidement avec rMax.
-
label : iso
type : nombre
titre : choix du tracé
Cette liste déroulante permet de choisir parmi les 3 tracés : iso-rayons, iso-redshifts, iso-flux. Pour l'image géométrique l'intensité de rouge code la distance radiale r au trou noir : plus un point est brillant plus il est proche du trou noir. Pour l'image du redshift le code de couleur est le code usuel : noir si z = 0, rouge si z > 0, bleu si z < 0. Pour l'image du flux l'intensité de rouge code l'intensité du flux (intégré) de photons.
-
label : casePrimaire
type : nombre
titre : image primaire
L'image primaire du disque est tracée ssi cette case est cochée.
-
label : caseSecondaire
type : nombre
titre : image secondaire
L'image secondaire du disque (rayons provenant de "sous" le disque) est tracée ssi cette case est cochée. Si la case "image primaire" est aussi cochée, seule la partie de l'image secondaire non cachée par l'image primaire est visible. Décocher la case "image primaire" permet de visualiser toute l'image (théorique) secondaire.
-
label : discretisationTheta
type : nombre
titre : pas de discrétisation de theta
L'angle de visée theta (angle entre la ligne de visée observateur - trou noir et la normale au disque d'accrétion) est automatiquement incrémenté au cours de la simulation. Ce curseur permet de régler son pas de discrétisation. Plus le curseur est vers la gauche, plus le pas est petit, donc plus la transition d'une image à l'autre est douce, mais plus il faut de temps (de calcul) pour faire un tour complet. Plus le curseur est vers la droite, plus le pas est grand, donc plus la rotation est rapide, mais plus les images sont saccadées. La valeur courante de theta est affichée sous l'image.
Mode d'emploi de l'applet
-
Image géométrique
Le tracé des iso-r permet de voir les effets purement géométriques de déformation du disque.
De face (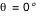 ou ou 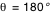 ) le disque circulaire apparait bien circulaire. L'inclinaison augmentant, il apparait comme une ellipse, ce qui est un simple effet de projection conforme à notre intuition. Mais lorsqu'on appoche de la tranche ( ) le disque circulaire apparait bien circulaire. L'inclinaison augmentant, il apparait comme une ellipse, ce qui est un simple effet de projection conforme à notre intuition. Mais lorsqu'on appoche de la tranche (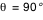 ou ou 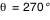 ) des effets purement relativistes apparaissent clairement. ) des effets purement relativistes apparaissent clairement.
- Tout d'abord l'image primaire se "tord" vers le haut, prenant une forme très caractéristique de chapeau mexicain : les photons partant du bord du disque le plus éloigné sont "ramenés" vers nous par la masse du trou noir, et ce bord "résiste" ainsi à disparaitre.
- D'autre part une image secondaire apparait du côté opposé, correspondant à la face normalement cachée du disque (mais dont les photons, qui partent en direction opposée à nous, sont là aussi "ramenés" vers nous par la masse du trou noir). Lorsqu'on observe le disque exactement par la tranche (
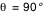 ou ou 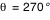 ), on ne voit que l'image secondaire qui forme un anneau d'Einstein. ), on ne voit que l'image secondaire qui forme un anneau d'Einstein.
On note qu'après un passage par la tranche (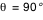 ou ou 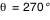 ) l'allure du disque se redéploie à l'identique mais est naturellement inversée. ) l'allure du disque se redéploie à l'identique mais est naturellement inversée.
Images géométriques du disque

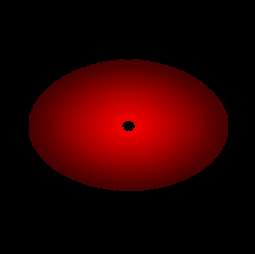






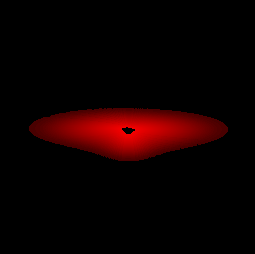
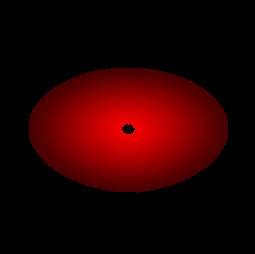
De gauche à droite et de haut en bas, theta = 0°, 50°, 80°, 87°, 88°, 90°, 93°, 94°, 102°, 127°
Crédit :
Jocelyn Couetdic, Gaelle Dumas, Gilles Ferrand
-
Carte du redshift
Le tracé des iso-z permet de mettre en évidence 2 effets de décalage spectral :
- de face (
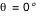 ou ou 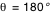 ) le disque est entièrement rouge, ce qui traduit un décalage positif : ) le disque est entièrement rouge, ce qui traduit un décalage positif : 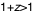 . Ceci est un effet de relativité générale du à la seule présence du trou noir : les photons émis vers nous doivent "lutter" pour s'échapper de son fort champ gravitationnel, d'où leur rougissement. . Ceci est un effet de relativité générale du à la seule présence du trou noir : les photons émis vers nous doivent "lutter" pour s'échapper de son fort champ gravitationnel, d'où leur rougissement.
- l'inclinaison augmentant, on voit apparaitre une dissymétrie gauche-droite qui traduit la rotation du disque : la partie bleue se rapproche de nous tandis que la partie rouge s'éloigne de nous. Lorsque
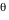 dépasse dépasse 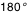 et et 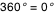 on note l'inversion gauche-droite des couleurs : on passe en effet alors de l' "autre côté" du disque. Dans tous les cas le côté rouge est plus intense que le côté bleu, ce qui est logique puisqu'on rajoute un effet équilibré sur un fond déjà rouge. on note l'inversion gauche-droite des couleurs : on passe en effet alors de l' "autre côté" du disque. Dans tous les cas le côté rouge est plus intense que le côté bleu, ce qui est logique puisqu'on rajoute un effet équilibré sur un fond déjà rouge.
Ces effets affectent l'image primaire comme l'image secondaire.
-
Photo du flux
Le tracé des iso-F donne une représentation réaliste de l'allure visuelle du disque.
Comme 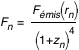 où où 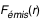 est une fonction décroissante de r, on observe le cumul des effets déjà observés pour r et pour z (de façon d'autant plus nette que l'on observe le disque en incidence rasante) : déformation des contours + dissymétrie gauche-droite. est une fonction décroissante de r, on observe le cumul des effets déjà observés pour r et pour z (de façon d'autant plus nette que l'on observe le disque en incidence rasante) : déformation des contours + dissymétrie gauche-droite.
Explications
Il s'agit de tracer l'image du disque sur la "plaque photo" d'un observateur situé à l'infini. Cette image est formée par les photons émis depuis la surface du disque. On profite du principe de retour inverse de la lumière pour la reconstituer en "lançant" un photon depuis chaque pixel de la plaque photo et en regardant à quel endroit du disque celui-ci tombe (s'il l'intercepte).
La trajectoire d'un photon (géodésique) ne dépend que du paramètre d'impact b (écart au centre de la plaque par rapport à la ligne de visée). Cela amène naturellement à décrire la plaque en coordonnées polaires (b, ). A b fixé, selon la valeur de ). A b fixé, selon la valeur de  seul change le point d'intersection de la géodésique avec le disque. D'où l'algorithme suivant : on discrétise le paramètre d'impact b de 0 à seul change le point d'intersection de la géodésique avec le disque. D'où l'algorithme suivant : on discrétise le paramètre d'impact b de 0 à 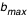 , où , où 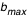 doit être choisi suffisamment grand pour avoir l'image complète du disque de rayon doit être choisi suffisamment grand pour avoir l'image complète du disque de rayon 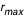 (de part l'effet de lentille gravitationnelle du trou noir, on a en effet (de part l'effet de lentille gravitationnelle du trou noir, on a en effet 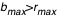 ; on peut prendre en première approximation ; on peut prendre en première approximation 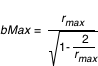 ). Pour chaque b : ). Pour chaque b :
- on discrétise
 sur 2 sur 2 de telle sorte que de telle sorte que 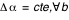 , ce qui amène à poser , ce qui amène à poser 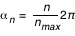 avec avec 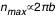
- on pré-calcule les valeurs des angles d'interception
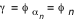 pour les différents pour les différents 
- on intègre la géodésique, c'est-à-dire qu'on incrémente
 en calculant le nouveau en calculant le nouveau 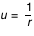 à chaque pas (par une méthode de Runge-Kutta, cf. la première applet de tracé des géodésiques). A chaque fois qu'on rencontre un à chaque pas (par une méthode de Runge-Kutta, cf. la première applet de tracé des géodésiques). A chaque fois qu'on rencontre un 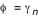 on relève la valeur du rayon d'impact on relève la valeur du rayon d'impact 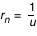 . Le pas adaptatif de l'intégrateur permet de détecter les . Le pas adaptatif de l'intégrateur permet de détecter les 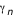 avec précision : le pas est constant au début ( avec précision : le pas est constant au début (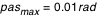 ), et dès que ), et dès que 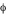 est plus proche que est plus proche que 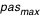 du prochain du prochain 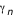 , on avance d'exactement , on avance d'exactement 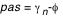 . Si . Si 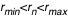 alors on a effectivement touché le disque. Sinon la valeur de alors on a effectivement touché le disque. Sinon la valeur de 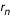 ne doit pas être relevée. Mais la géodésique a alors une seconde chance d'impact après un demi-tour du disque, à ne doit pas être relevée. Mais la géodésique a alors une seconde chance d'impact après un demi-tour du disque, à 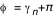 . Si alors . Si alors 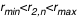 on obtient un point on obtient un point 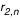 pour l'image secondaire.
L'intégration de la géodésique (avance de pour l'image secondaire.
L'intégration de la géodésique (avance de 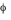 ) est arrêtée lorsqu'on sort du cadre du tracé. ) est arrêtée lorsqu'on sort du cadre du tracé.
- Si on veut tracer le redshift on calcule
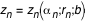 . .
- Si on veut tracer le flux (observé) on calcule
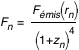
A la fin de cette étape on dispose d'un cercle entier (à  ) de valeurs de r (ou de z ou de F) qu'on projette sur une grille cartésienne (x,y) (coordonnées naturelles de l'image affichée par Simulab). On dispose en fait de 2 jeux de valeurs ) de valeurs de r (ou de z ou de F) qu'on projette sur une grille cartésienne (x,y) (coordonnées naturelles de l'image affichée par Simulab). On dispose en fait de 2 jeux de valeurs 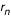 et et 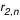 (ou (ou 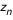 et et 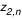 ou ou 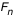 et et 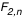 ), pour l'image primaire et l'image secondaire. On utilise l'un ou l'autre selon que la case "image primaire" ou "image secondaire" est cochée, et on réalise un OU exclusif si les 2 cases sont cochées (cad que l'image secondaire ne peut apparaitre là où il y a déjà une image primaire).
La répétition de ce procédé sur tous les b jusqu'à ), pour l'image primaire et l'image secondaire. On utilise l'un ou l'autre selon que la case "image primaire" ou "image secondaire" est cochée, et on réalise un OU exclusif si les 2 cases sont cochées (cad que l'image secondaire ne peut apparaitre là où il y a déjà une image primaire).
La répétition de ce procédé sur tous les b jusqu'à  permet de reconstituer toute l'image sur la plaque photo. permet de reconstituer toute l'image sur la plaque photo.
Tout ce calcul est effectué pour un angle de visée 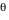 donné (angle entre la ligne de visée et la normale au disque d'accrétion). Dès qu'une image complète a été calculée, le calcul est repris (automatiquement, par Simulab) pour une nouvelle valeur de donné (angle entre la ligne de visée et la normale au disque d'accrétion). Dès qu'une image complète a été calculée, le calcul est repris (automatiquement, par Simulab) pour une nouvelle valeur de 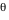 . Cet angle est discrétisé sur 360° de façon non linéaire, de sorte que plus d'images soient calculées aux abords des incidences rasantes . Cet angle est discrétisé sur 360° de façon non linéaire, de sorte que plus d'images soient calculées aux abords des incidences rasantes 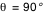 et et 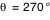 où les effets relativistes sont les plus notables. Ainsi pour où les effets relativistes sont les plus notables. Ainsi pour 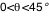 , , 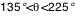 et et 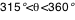 on avance avec un pas on avance avec un pas 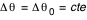 (fixé par le curseur entre 5° et 45°), et pour (fixé par le curseur entre 5° et 45°), et pour 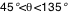 et et 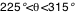 on a on a 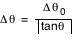 . .
|
 ). A b fixé, selon la valeur de
). A b fixé, selon la valeur de  seul change le point d'intersection de la géodésique avec le disque. D'où l'algorithme suivant : on discrétise le paramètre d'impact b de 0 à
seul change le point d'intersection de la géodésique avec le disque. D'où l'algorithme suivant : on discrétise le paramètre d'impact b de 0 à 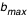 , où
, où 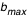 doit être choisi suffisamment grand pour avoir l'image complète du disque de rayon
doit être choisi suffisamment grand pour avoir l'image complète du disque de rayon 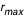 (de part l'effet de lentille gravitationnelle du trou noir, on a en effet
(de part l'effet de lentille gravitationnelle du trou noir, on a en effet 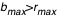 ; on peut prendre en première approximation
; on peut prendre en première approximation 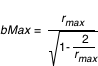 ). Pour chaque b :
). Pour chaque b :
 ) de valeurs de r (ou de z ou de F) qu'on projette sur une grille cartésienne (x,y) (coordonnées naturelles de l'image affichée par Simulab). On dispose en fait de 2 jeux de valeurs
) de valeurs de r (ou de z ou de F) qu'on projette sur une grille cartésienne (x,y) (coordonnées naturelles de l'image affichée par Simulab). On dispose en fait de 2 jeux de valeurs 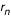 et
et 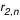 (ou
(ou 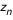 et
et 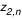 ou
ou 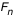 et
et 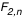 ), pour l'image primaire et l'image secondaire. On utilise l'un ou l'autre selon que la case "image primaire" ou "image secondaire" est cochée, et on réalise un OU exclusif si les 2 cases sont cochées (cad que l'image secondaire ne peut apparaitre là où il y a déjà une image primaire).
La répétition de ce procédé sur tous les b jusqu'à
), pour l'image primaire et l'image secondaire. On utilise l'un ou l'autre selon que la case "image primaire" ou "image secondaire" est cochée, et on réalise un OU exclusif si les 2 cases sont cochées (cad que l'image secondaire ne peut apparaitre là où il y a déjà une image primaire).
La répétition de ce procédé sur tous les b jusqu'à  permet de reconstituer toute l'image sur la plaque photo.
permet de reconstituer toute l'image sur la plaque photo.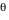 donné (angle entre la ligne de visée et la normale au disque d'accrétion). Dès qu'une image complète a été calculée, le calcul est repris (automatiquement, par Simulab) pour une nouvelle valeur de
donné (angle entre la ligne de visée et la normale au disque d'accrétion). Dès qu'une image complète a été calculée, le calcul est repris (automatiquement, par Simulab) pour une nouvelle valeur de 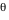 . Cet angle est discrétisé sur 360° de façon non linéaire, de sorte que plus d'images soient calculées aux abords des incidences rasantes
. Cet angle est discrétisé sur 360° de façon non linéaire, de sorte que plus d'images soient calculées aux abords des incidences rasantes 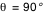 et
et 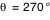 où les effets relativistes sont les plus notables. Ainsi pour
où les effets relativistes sont les plus notables. Ainsi pour 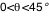 ,
, 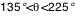 et
et 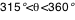 on avance avec un pas
on avance avec un pas 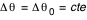 (fixé par le curseur entre 5° et 45°), et pour
(fixé par le curseur entre 5° et 45°), et pour 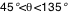 et
et 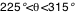 on a
on a 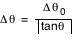 .
.
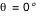 ou
ou 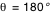 ) le disque circulaire apparait bien circulaire. L'inclinaison augmentant, il apparait comme une ellipse, ce qui est un simple effet de projection conforme à notre intuition. Mais lorsqu'on appoche de la tranche (
) le disque circulaire apparait bien circulaire. L'inclinaison augmentant, il apparait comme une ellipse, ce qui est un simple effet de projection conforme à notre intuition. Mais lorsqu'on appoche de la tranche (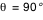 ou
ou 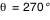 ) des effets purement relativistes apparaissent clairement.
) des effets purement relativistes apparaissent clairement.
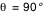 ou
ou 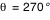 ), on ne voit que l'image secondaire qui forme un anneau d'Einstein.
), on ne voit que l'image secondaire qui forme un anneau d'Einstein.









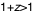 . Ceci est un effet de relativité générale du à la seule présence du trou noir : les photons émis vers nous doivent "lutter" pour s'échapper de son fort champ gravitationnel, d'où leur rougissement.
. Ceci est un effet de relativité générale du à la seule présence du trou noir : les photons émis vers nous doivent "lutter" pour s'échapper de son fort champ gravitationnel, d'où leur rougissement.
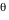 dépasse
dépasse 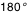 et
et 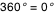 on note l'inversion gauche-droite des couleurs : on passe en effet alors de l' "autre côté" du disque. Dans tous les cas le côté rouge est plus intense que le côté bleu, ce qui est logique puisqu'on rajoute un effet équilibré sur un fond déjà rouge.
on note l'inversion gauche-droite des couleurs : on passe en effet alors de l' "autre côté" du disque. Dans tous les cas le côté rouge est plus intense que le côté bleu, ce qui est logique puisqu'on rajoute un effet équilibré sur un fond déjà rouge. 
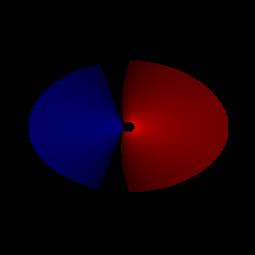


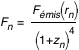 où
où 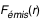 est une fonction décroissante de r, on observe le cumul des effets déjà observés pour r et pour z (de façon d'autant plus nette que l'on observe le disque en incidence rasante) : déformation des contours + dissymétrie gauche-droite.
est une fonction décroissante de r, on observe le cumul des effets déjà observés pour r et pour z (de façon d'autant plus nette que l'on observe le disque en incidence rasante) : déformation des contours + dissymétrie gauche-droite.
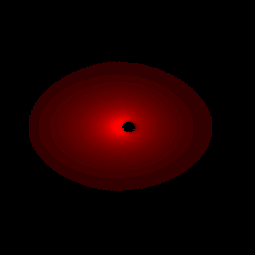




 de telle sorte que
de telle sorte que 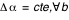 , ce qui amène à poser
, ce qui amène à poser 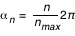 avec
avec 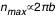
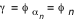 pour les différents
pour les différents  en calculant le nouveau
en calculant le nouveau 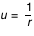 à chaque pas (par une méthode de Runge-Kutta, cf. la première applet de tracé des géodésiques). A chaque fois qu'on rencontre un
à chaque pas (par une méthode de Runge-Kutta, cf. la première applet de tracé des géodésiques). A chaque fois qu'on rencontre un 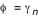 on relève la valeur du rayon d'impact
on relève la valeur du rayon d'impact 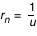 . Le pas adaptatif de l'intégrateur permet de détecter les
. Le pas adaptatif de l'intégrateur permet de détecter les 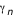 avec précision : le pas est constant au début (
avec précision : le pas est constant au début (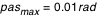 ), et dès que
), et dès que 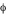 est plus proche que
est plus proche que 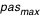 du prochain
du prochain 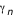 , on avance d'exactement
, on avance d'exactement 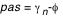 . Si
. Si 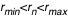 alors on a effectivement touché le disque. Sinon la valeur de
alors on a effectivement touché le disque. Sinon la valeur de 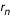 ne doit pas être relevée. Mais la géodésique a alors une seconde chance d'impact après un demi-tour du disque, à
ne doit pas être relevée. Mais la géodésique a alors une seconde chance d'impact après un demi-tour du disque, à 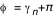 . Si alors
. Si alors 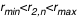 on obtient un point
on obtient un point 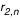 pour l'image secondaire.
L'intégration de la géodésique (avance de
pour l'image secondaire.
L'intégration de la géodésique (avance de 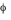 ) est arrêtée lorsqu'on sort du cadre du tracé.
) est arrêtée lorsqu'on sort du cadre du tracé. 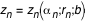 .
.