Spectre de rayonnement de Corps Noir
Auteur: Marc Huertas
Auteur: Leroi Vaitua
Date de création : 18 Janvier 2005
Date de mise à jour : 18/01/2004
Introduction
Cette applet permet de visualiser le spectre d'émission d'un corps noir suivant sa température. Le corps noir modélise un objet idéal qui absorberait toute l'énergie électromagnétique qu'il reçoit, sans en réfléchir ou en transmettre. Plusieurs choix sont offerts :
- Corps Noir Fréquence : on visualise le corps noir en fréquence
- Corps Noir Lambda : on visualise le corps noir en longueur d'onde
Liste des paramètres de l'applet
-
label : temperature
type : nombre
titre : temperature du corps noir
unités : K
Ce paramètre indique la température du corps noir que vous considérez. Par exemple le soleil est un corps noirs à 5600K
-
label : log
type : string
titre : echelle logarithmique
Cocher la case si vous désirez que les valeurs soient en échelle logarithmique. Attention, il est conseillé d'éffacer les graphiques précédent avant de paser en échelle logarithmique compte tenu des changements d'échelles assez importants...
Mode d'emploi de l'applet
L'applet permet de visualiser la courbe d'émission d'un corps noir à la température fixée au départ par l'utilisateur. Plusieurs modes d'affichage sont disponibles (Courbe en fréquence, longueur d'onde, données normales ou logarithmiques).
De plus, en ce qui concerne l'affichage en longueur d'onde, une image de fond représentant le spectre de la lumière visible permet de voir comment se situe l'émission du corps noir par rapport à celui-ci.
On peut voir sur la figure ci-dessous un exemple de corps noir ayant une température de 5500 K :
Remarque :
On précise que les unites de l'axe des ordonnées représentent l'amplitude de l'émssion du corps noir. Cependant, cet axe ne donne qu'une idée qualitative du spectre et non quantitative. On a donc l'aspect générale de la courbe mais il ne faut pas trop tenir compte des valeurs...
Explications
Afin de modéliser le corps noir, on s'est servi de la loi de planck. Cette loi s'exprime est la suivante :
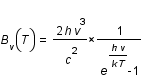
Remarque :
Les formules sont ici exprimées en fréquence, le lecteur pourra à titre d'exercice tenter d'exprimer des relations en longueur d'onde... On rappelera qu'il faut partir de la relation 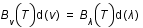 et non pas exprimer directement la fréquence en fonction de la longueur d'onde dans et non pas exprimer directement la fréquence en fonction de la longueur d'onde dans 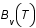 . On obtient ainsi la relation suivante : . On obtient ainsi la relation suivante :
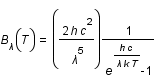
|