Spectre d'un disque d'accretion autour d'un trou noir
Auteur: Marc Huertas
Auteur: Vaitua Leroi
Date de création : 01/01/2005
Introduction
Cette applet permet de visualiser la carte du Redshift d'un disque d'accretion géométriquement fin et optiquement épais en rotation képlérienne autour d'un trou noir de Schwarzschild ainsi que le spectre associé en suposant l'émission monochromatique. La visualisation peut se réaliser de deux manières :
- Dynamique : on trace le spectre du disque suivant différents angles de vues successifs
- Statique : on choisit un angle de vue et l'applet calcul et affiche le spectre résultant
Un point important est à signaler : celui du temps de calcul... En effet, les équations à intégrer étant passablement compliquées, ne vous inquietez pas si vous avez un certain temps d'attente avant de voir s'afficher les résultats.
Rappels de cours
Il existe d'autres appliquettes qui permettent de visualiser différentes caractéristiques du trou noir (son image géométrique iso-r, la carte du redshift iso-z (seule), la "photo" du flux(bolométrique) iso-F). Une introduction aux différents phénomènes physique mis en jeu est présentée dans les cours.
Liste des paramètres de l'applet
-
label : rMax
type : nombre
titre : rayon externe du disque
unités : ua
C'est le rayon maximal du disque d'accrétion
-
label : casePrimaire
type : string
titre : image primaire
Cocher cette case pour sélectionner l'image primaire du disque.
-
label : caseSecondaire
type : string
titre : image secondaire
Cocher cette case pour sélectionner l'image secondaire du disque.
-
label : pasfrequence
type : nombre
titre : pas en fréquence
unités : s
Ce paramètre règle le pas d'échantillonage en temps. Plus le pas est petit, plus vous aurez de points mais le temps de calcul s'en trouvera rallongé...
-
label : SN
type : nombre
titre : Rapport Signal sur Bruit
Ce paramètre augmente le rapport signal sur bruit en augmentant l'échantillonage spatial. Cependant, faites attention car plus l'échantillonage est important, plus le temps de calcul est important...
-
label : discretisationTheta
type : nombre
titre : Pas de discrétisation de l'angle de visée (valable en dynamique uniquement)
Ce curseur permet de définir le pas de l'angle de vue du disque.
-
label : theta
type : nombre
titre : angle de visee (valable uniquement en statique)
Ce paramètre permet de fixer dans le mode statique l'angle sous lequel est vu le disque.
-
label : norm
type : string
titre : normalisation
Cocher cette case permet de normaliser tous les spectres obtenus.
Mode d'emploi de l'applet
L'applet permet de visualiser la carte du redshift ainsi que le spectre résultant. L'applet permet de visualiser (dans le mode dynamique uniquement) l'évolution du spectres avec l'angle de visée.
Une description détaillée existe et permet l'analyse de la carte du redshift. Vous pouvez la trouver parmi les autres appliquettes du campus numérique.
Le spectre du disque présente différents aspect :
- Au départ, pour
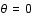 , le spectre présente un seul pic étalé en fréquence. Ceci est du au redshift qui varie quand on s'éloigne du centre , le spectre présente un seul pic étalé en fréquence. Ceci est du au redshift qui varie quand on s'éloigne du centre
- Lorsque l'inclinaison augmente, ce pic se dédouble de part et d'autre du pic initial. Ceci met en valeur la rotation du disque avec une partie se rapprochant de l'observateur et l'autre s'éloignant.
Afin d'illustrer l'applet, voici une série de simulation, réalisée pour différents 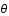 , avec un rayon de 100, avec un rapport signal sur bruit par defaut.
Exemple d'utilisation
Afin d'illustrer nos propos, voici une application commentée de l'applet. Tout d'abord il faut choisir les différent paramètre. Ceux-ci peuvent être choisi directement. Une fois ces paramêtres réglés, l'applet peut être lancée.
Les différents paramêtres disponibles
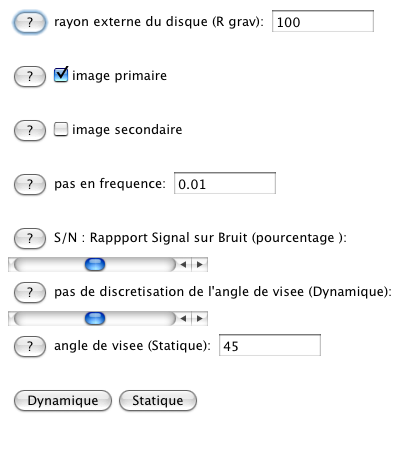 Crédit :
Crédit :
Huertas Marc et Leroi Vaitua
Une fois l'applet lancée et exécutée on voit les graphiques s'afficher les uns après les autres. La figure ci-dessous montre l'affichage des résultats après un temps de fonctionnement.
Spectres
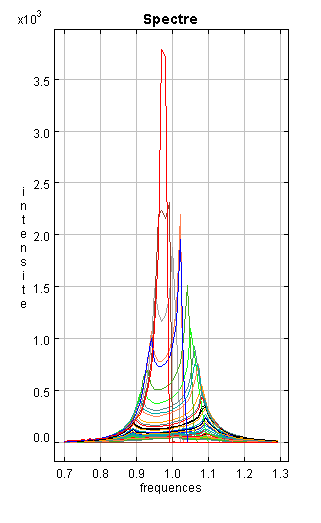
L'évolution des spectres suivant l'angle de visée.
|
Crédit :
Marc huertas et Vaitua Leroi
Remarque :
Le problème de qualité des spectres
On constate une dégradation de la qualité du spectre avec l'angle de visée. Cet effet est uniquement dû à l'échantillonage de l'image du disque. En effet, le nombre de point d'échantillonage fixe le rapport signal sur bruit. Plus on aura de points, plus la qualité du spectre sera bonne. Cependant, l'échantillonage reste constant tout au long du déroulement du programme et le disque s'amincit (jusqu'à être vu par la tranche ! ). Le nombre de points varie ce qui explique cette dégradation. On peut améliorer la qualité des spectres en augmentant les différents paramètres d'échantillonage. Cependant la rapidité d'exécution s'en trouve affectée d'autant...
Explications
Il s'agit de tracer le spectre integré de la surface du disque en rotation autour du trou noir. On a donc besoin de connaître l'intensité reçue au niveau de l'observateur à chaque fréquence, ce qui revient en définitive à modéliser un spectrographe.
Ainsi, il est necessaire de faire une première hypothèse concernant le
mode d'emission du disque. Pour cela, on a décidé en une première
approximation, de supposer que chaque point du disque emet une raie
infiniment fine à la fréquence de référence 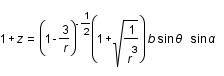 et que l'amplitude
de celle ci est modulée par un facteur d'atténuation radial 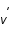
, où r est la distance au trou noir.
Ce modèle, bien que simpliste permet de retrouver les allures typiques de ce type de spectres d'émission.
Par conséquent, d'après l'article de J.P Luminet, l'intensité reçue est de la forme:
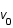
On observe que l'expression est gouvernée fondamentalement par un facteur de redshift 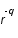 provenant des divers effets Doppler liés au mouvement du disque. En effet, on a, d'une part la contribution cinématique due à la rotation de celui-ci et d'autre part l'effet relativiste de la gravité du trou noir.
Ainsi, ce facteur peut être déterminé à l'aide de l'expression suivante, tirée à nouveau de l'article de J.P Luminet.
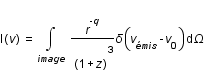
On constate, en analysant l'équation ci dessus, que le redshift dépend essentiellement de la distance r au centre du disque, du paramètre d'impact b ainsi que des angles d'inclinaison et de repérage dans le récepteur. Ainsi, pour connaître le redshift associé à un point (b, alpha) du spectrographe, il suffit de connaître la distance radiale r du point d'où provient le rayon lumnineux.
En utilisant le principe de retour inverse de la lumière, ceci revient à integrer une géodésique dans l'espace metrique de Schwarzschild associé à la présence du trou noir.
Ainsi, la réalisation du spectrographe peut se décomposer en 2 étapes:
- Integration géodésique. Pour cela on parcours l'image 2D du disque en coordonnées polaires (b,
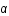 ), on intègre la géodésique associée et on en déduit la distance d'impact r, qui est stockée dans un vecteur. ), on intègre la géodésique associée et on en déduit la distance d'impact r, qui est stockée dans un vecteur.
- Construction du spectre. À l'aide de l'expression de Luminet, on calcule le redshift associé à chaque point et donc la fréquence reçue
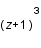 en chacun de ces points du spectrographe. en chacun de ces points du spectrographe.
Remarque :
En ce qui concerne la résolution et la bande passante du spectrographe
Comme tout spectrographe, le modèle possède une résolution et une bande passante propres qui ont été reglés de façon quasi empirique.
En effet, la résolution est déterminée exclusivement par le pas d'echantillonnage en fréquence lors de la construction du spectre: un échantillonnage trop grossier intègre trop de flux dans un même rang spectral et noie donc les détails du spectre, et au contraire, un échantillonnage trop fin nécessite d'un temps de calcul élevé et est moins robuste au bruit car le flux reçu par intervalle frequentiel est trop petit.
La bande passante doit etre fixée de façon à pouvoir visualiser le spectre dans sa totalité. On pourrait être tenté de penser que les décalages maximaux et minimaux proviennent des régions extrèmes du disque. Ceci n'est pas cependant toujours vrai, et la détermination de ces valeurs limites n'est pas du tout évidente.
Afin de compléter notre explication concernant la programmation numérique de l'applet, on pourra regarder la figure ci-dessous qui résume l'utilisation des variables.
|