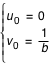Métrique et géodésique
On se place dans le cadre de la métrique de Schwarzschild:
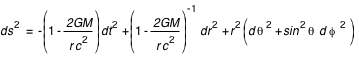
M est la masse du trou noir. Pour simplifier les équations, on prendra G=1 et c=1. Dans ces unités, l'horizon du trou noir est défini par le rayon de Schwarzschild
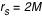
. On prendra désormais M=1.
De plus, les géodésiques des photons sont toutes dans un même plan, on se restreint donc à l'étude dans un plan, par exemple celui tel que
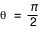
. Pour des photons
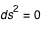
, on a donc l'équation suivante pour les géodésiques autour du trou noir:
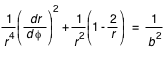
, où b est le paramètre d'impact à l'infini.
On va à présent adimensionner les grandeurs. On prend comme échelle de longueur le rayon gravitationnel,
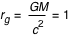
(comme G=1, c=1 et M=1). Donc on choisit la variable
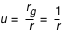
, sans dimension. L'équation devient alors:
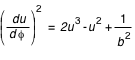
, équation non linéaire à résoudre pour avoir les géodésiques u(

) des photons.
Etude du second membre
Récrivons l'équation des géodésiques:
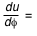
±
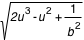
. Au début de la trajectoire, l'angle

augmente, donc u augmente et on utilise la première solution avec un signe + (la dérivée de u par rapport à

est positive). Mais, après le périastre,

diminue et on change de solution: la deuxième équation, avec le signe -. Il y a donc 2 problèmes:
- y a-t'il un périastre?
- s'il existe, il faut le trouver et changer de solution.
Ainsi, pour des paramètre d'impacts trop faibles, on ne passe jamais par un périastre et le photon tombe sous l'horizon du trou noir. Au contraire, quand b est assez grand, la trajectoire du photon est déviée par le trou noir, et il continue à l'infini. Donc il existe une valeur du paramètre d'impact qui traduit ce changement de comportement: le paramètre critique
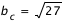
. Pour
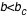
, le photon tombe dans le trou noir et pour
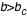
, il est dévié sans être capturé.
Il y a donc une discontinuité dans la résolution de l'équation des géodésiques. Pour s'affranchir de ce problème, on dérive l'équation des géodésiques par rapport à

:
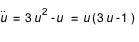
, avec
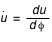
.
Donc, on doit résoudre le système d'équation:
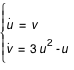
avec les conditions initiales suivantes :
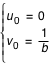

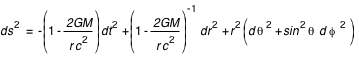
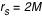 . On prendra désormais M=1.
De plus, les géodésiques des photons sont toutes dans un même plan, on se restreint donc à l'étude dans un plan, par exemple celui tel que
. On prendra désormais M=1.
De plus, les géodésiques des photons sont toutes dans un même plan, on se restreint donc à l'étude dans un plan, par exemple celui tel que 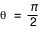 . Pour des photons
. Pour des photons 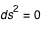 , on a donc l'équation suivante pour les géodésiques autour du trou noir:
, on a donc l'équation suivante pour les géodésiques autour du trou noir:
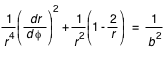 , où b est le paramètre d'impact à l'infini.
, où b est le paramètre d'impact à l'infini.
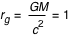 (comme G=1, c=1 et M=1). Donc on choisit la variable
(comme G=1, c=1 et M=1). Donc on choisit la variable 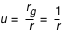 , sans dimension. L'équation devient alors:
, sans dimension. L'équation devient alors: 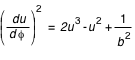 , équation non linéaire à résoudre pour avoir les géodésiques u(
, équation non linéaire à résoudre pour avoir les géodésiques u( ) des photons.
) des photons.
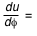 ±
±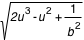 . Au début de la trajectoire, l'angle
. Au début de la trajectoire, l'angle  augmente, donc u augmente et on utilise la première solution avec un signe + (la dérivée de u par rapport à
augmente, donc u augmente et on utilise la première solution avec un signe + (la dérivée de u par rapport à  est positive). Mais, après le périastre,
est positive). Mais, après le périastre,  diminue et on change de solution: la deuxième équation, avec le signe -. Il y a donc 2 problèmes:
diminue et on change de solution: la deuxième équation, avec le signe -. Il y a donc 2 problèmes: 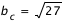 . Pour
. Pour 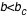 , le photon tombe dans le trou noir et pour
, le photon tombe dans le trou noir et pour 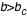 , il est dévié sans être capturé.
Il y a donc une discontinuité dans la résolution de l'équation des géodésiques. Pour s'affranchir de ce problème, on dérive l'équation des géodésiques par rapport à
, il est dévié sans être capturé.
Il y a donc une discontinuité dans la résolution de l'équation des géodésiques. Pour s'affranchir de ce problème, on dérive l'équation des géodésiques par rapport à  :
:
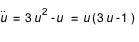 , avec
, avec 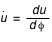 .
.
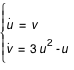 avec les conditions initiales suivantes :
avec les conditions initiales suivantes :