Détermination du disque.
Tout le calcul des géodésiques qui vient d'être effectué permet de déterminer l'image du disque d'accrétion vu par l'observateur situé à l'infini.
L'angle

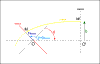
est défini comme l'angle entre la ligne de visée (OO') et la normale au plan du disque.
Sur la figure précédente, on voit que le point M du disque donne une image primaire sur le détecteur en M'. Il existe aussi une image secondaire de M, comme on peut le voir sur la figure suivante:
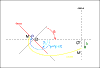
Ainsi, on voit que l'image primaire est donnée par un angle d'intersection
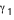
et que l'image secondaire est donnée par l'angle
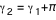
.
Il nous reste alors à déterminer l'angle d'intersection du disque et de la géodésique,
. Sur la figure suivante, on peut voir la géométrie de l'ensemble de la configuration:
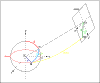
Pour déterminer l'angle
, on se place dans le triangle sphérique MYY'. Et on trouve:
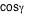
= ±
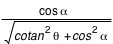
. Le signe dépend de

: si
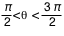
, alors on prend le signe -, sinon, c'est le signe +.
Connaissant
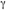
, on déduit la position r(
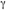
,b) sur le disque en intégrant l'équation des géodésiques, et on trace ainsi l'image géométrique du disque. Il faut noter qu'il n'y a réellement impact des photons sur le disque que si r est compris entre
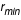
et
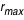
.
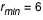
, en dessous il n'existe pas d'orbite stable autour du trou noir.
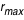
est le rayon externe du disque.

 est défini comme l'angle entre la ligne de visée (OO') et la normale au plan du disque.
Sur la figure précédente, on voit que le point M du disque donne une image primaire sur le détecteur en M'. Il existe aussi une image secondaire de M, comme on peut le voir sur la figure suivante:
est défini comme l'angle entre la ligne de visée (OO') et la normale au plan du disque.
Sur la figure précédente, on voit que le point M du disque donne une image primaire sur le détecteur en M'. Il existe aussi une image secondaire de M, comme on peut le voir sur la figure suivante:
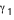 et que l'image secondaire est donnée par l'angle
et que l'image secondaire est donnée par l'angle 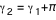 .
.
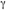 . Sur la figure suivante, on peut voir la géométrie de l'ensemble de la configuration:
. Sur la figure suivante, on peut voir la géométrie de l'ensemble de la configuration:
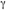 , on se place dans le triangle sphérique MYY'. Et on trouve:
, on se place dans le triangle sphérique MYY'. Et on trouve:
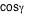 = ±
= ± 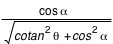 . Le signe dépend de
. Le signe dépend de  : si
: si 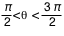 , alors on prend le signe -, sinon, c'est le signe +.
Connaissant
, alors on prend le signe -, sinon, c'est le signe +.
Connaissant 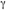 , on déduit la position r(
, on déduit la position r(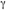 ,b) sur le disque en intégrant l'équation des géodésiques, et on trace ainsi l'image géométrique du disque. Il faut noter qu'il n'y a réellement impact des photons sur le disque que si r est compris entre
,b) sur le disque en intégrant l'équation des géodésiques, et on trace ainsi l'image géométrique du disque. Il faut noter qu'il n'y a réellement impact des photons sur le disque que si r est compris entre 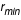 et
et 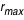 .
. 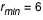 , en dessous il n'existe pas d'orbite stable autour du trou noir.
, en dessous il n'existe pas d'orbite stable autour du trou noir. 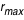 est le rayon externe du disque.
est le rayon externe du disque.