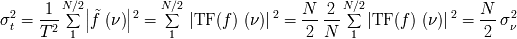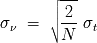, y teniendo en cuenta las propiedades de la TF, tenemos:
, y teniendo en cuenta las propiedades de la TF, tenemos:
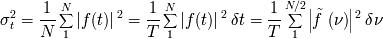
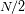 frecuencias reales entre las frecuencias nulas y
frecuencias reales entre las frecuencias nulas y
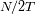 .
Con el cambio de notación:
.
Con el cambio de notación:
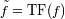 , y teniendo en cuenta que
, y teniendo en cuenta que
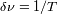 :
: