 Ejercicio 'Compresión gravitacional'
Ejercicio 'Compresión gravitacional'
Nivel ***
Tiempo necesario :
30 min
El objetivo del ejercicio es de estimar la constante de proporcionalidad de la
compresión gravitacional. Vamos a suponer un modelo de distribución de masa volúmica simple
pero que tiene en cuenta las altas densidades en el interior del planeta :
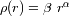
.
Vamos a utilizar exponentes negativos. Estos exponentes conducen a una singularidad en el
centro pero en nuestro caso no tiene consecuencias.
1)
Determinar la relación entre la masa total
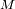
y el radio exterior
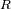
. Deducir la expresión del coeficiente
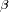
en función de estas magnitudes.
ayuda
solución
2)
Deducir la masa
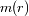
y el campo gravitacional en un punto de radio

. ¿Qué condición en el exponente

garantiza que el campo no diverge?
ayuda
ayuda
solución
3)
El equilibrio hidrostático da el gradiente de presión :
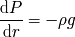
Deducir la presión central.
ayuda
solución
4)
Discutir de la forma del resultado anterior. ¿ Qué pasaría para una distribución no uniforme
?
ayuda
ayuda
solución
 Ejercicio '....'
Ejercicio '....'
Nivel **
Tiempo necesario :
30 min

El objetivo del ejercicio es de modelizar la altura límite de una montaña sobre un planeta de
masa
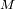
y radio
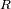
, para deducir la transición entre un objeto esférico y un objeto que se parezca más a un cacahuete,
como los núcleos cometarios.
Se supone la montaña de forma cilíndrica, de sección
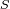
y altura

, en el campo gravitacional del planeta.
1)
¿ Cuál es la expresión del campo gravitacional

. Determinar la energía suplementaria para añadir a la cumbre una masa
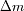
, en función de

y

.
ayuda
solución
2)
Deducir el valor límite de la altura

, para el cual la capa añadida en la cumbre conduce a derretir una capa equivalente a la base de la
montaña. Expresar en función del calor latente de fusión de las rocas
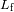
. Hacer la aplicación numérica para la Tierra, con
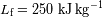
.
ayuda
solución
3)
Las más altas montañas en la Tierra alcanzan 8.8 km en la Tierra (el Everest) y 27 en Marte (el monte
Olimpo). Con la ayuda de los datos del calcotrón, verificar si la estimación precedente es
correcta.
solución
4)
Suponiendo válido el resultado anterior y denotando

la masa volúmica uniforme del planeta, deducir el radio mínimo de un planeta esférico con montañas de
altura igual al radio del planeta. Hacer la aplicación numérica con la masa volúmica de la corteza
terrestre de
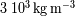
.
ayuda
solución

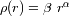 .
.
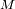 y el radio exterior
y el radio exterior
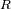 . Deducir la expresión del coeficiente
. Deducir la expresión del coeficiente
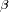 en función de estas magnitudes.
ayuda
solución
en función de estas magnitudes.
ayuda
solución
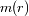 y el campo gravitacional en un punto de radio
y el campo gravitacional en un punto de radio
 . ¿Qué condición en el exponente
. ¿Qué condición en el exponente
 garantiza que el campo no diverge?
ayuda
ayuda
solución
garantiza que el campo no diverge?
ayuda
ayuda
solución
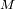 y radio
y radio
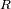 , para deducir la transición entre un objeto esférico y un objeto que se parezca más a un cacahuete,
como los núcleos cometarios.
, para deducir la transición entre un objeto esférico y un objeto que se parezca más a un cacahuete,
como los núcleos cometarios.
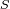 y altura
y altura
 , en el campo gravitacional del planeta.
, en el campo gravitacional del planeta.
 . Determinar la energía suplementaria para añadir a la cumbre una masa
. Determinar la energía suplementaria para añadir a la cumbre una masa
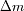 , en función de
, en función de
 y
y
 .
ayuda
solución
.
ayuda
solución
 , para el cual la capa añadida en la cumbre conduce a derretir una capa equivalente a la base de la
montaña. Expresar en función del calor latente de fusión de las rocas
, para el cual la capa añadida en la cumbre conduce a derretir una capa equivalente a la base de la
montaña. Expresar en función del calor latente de fusión de las rocas
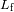 . Hacer la aplicación numérica para la Tierra, con
. Hacer la aplicación numérica para la Tierra, con
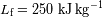 .
ayuda
solución
.
ayuda
solución