Magnitud absoluta
La magnitud absoluta
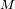
es la magnitud convencional que tendría la estrella si su distancia fuese llevada a 10pc.
Para ello se relaciona el brillo aparente de la estrella y su distancia

a la Tierra. Se obtiene de esa manera la
luminosidad
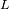
de la estrella que mide la potencia total radiada :
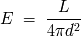
El flujo de una estrella varía con la inversa del cuadrado de la distancia, por lo tanto en un sistema
de magnitud dado, la relación entre las magnitudes absolutas y aparentes se escribe
:
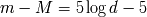 Magnitudes aparentes y absolutas
Magnitudes aparentes y absolutas
| Objeto |

|
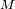
|
 (pc)
(pc) |
| Sol |
-26.7 |
4.9 |
|
| Sirio |
-1.45 |
1.4 |
2.7 |
| Vega |
0.00 |
0.5 |
8.1 |
| Antares |
1.00 |
-4.8 |
130 |
| Mimosa |
1.26 |
-4.7 |
150 |
| Adhara |
1.50 |
-5.0 |
200 |
El módulo de la distancia
La cantidad

se llama el
modulo de distancia. El modulo une la distancia a una diferencia de magnitud.
Indica la distancia en escala logarítmica.
Modulo de distancia
| Objeto |
módulo de distancia |
distancia al Sol (pc) |
| référence |
0 |
10 |
| Cúmulo de las Hyades |
3.3 |
48 |
| Las nubes de Magallanes |
18.5 |
50 000 |
| La galaxia de Andrómeda |
24.1 |
890 000 |
El módulo de distancia es nulo, por definición, para una distancia de 10 pc ; vale 5 para una distancia
de 100 pc, 10 para una distancia de 1000 pc.
Corrección de la absorción
Para pasar de la magnitud aparente a la magnitud absoluta, se tiene que corregir, además de
la distancia, los efectos debidos a la absorción interestelar. Esta absorción es provocada por
diversos elementos (polvo, gas) presentes en la línea de mira. La magnitud absoluta se expresa
en función de la magnitud aparente por :
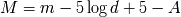
El término de absorción
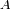
tiene que ser positivo; no tenerlo en cuenta conduce a sobreestimar la magnitud absoluta, o
sea a subestimar la luminosidad del objeto.
Magnitud bolométrica
Al contrario de la magnitud monocromática, la magnitud bolométrica mide la energía radiada
en todo el espectro electromagnético. Medir tal magnitud no es fácil. Se obtiene en general por
extrapolación de la magnitud absoluta medida en varias bandas espectrales.

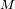 es la magnitud convencional que tendría la estrella si su distancia fuese llevada a 10pc.
es la magnitud convencional que tendría la estrella si su distancia fuese llevada a 10pc.
 a la Tierra. Se obtiene de esa manera la luminosidad
a la Tierra. Se obtiene de esa manera la luminosidad
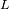 de la estrella que mide la potencia total radiada :
de la estrella que mide la potencia total radiada :
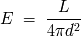
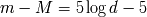

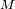
 (pc)
(pc) se llama el modulo de distancia. El modulo une la distancia a una diferencia de magnitud.
Indica la distancia en escala logarítmica.
se llama el modulo de distancia. El modulo une la distancia a una diferencia de magnitud.
Indica la distancia en escala logarítmica.
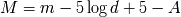
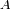 tiene que ser positivo; no tenerlo en cuenta conduce a sobreestimar la magnitud absoluta, o
sea a subestimar la luminosidad del objeto.
tiene que ser positivo; no tenerlo en cuenta conduce a sobreestimar la magnitud absoluta, o
sea a subestimar la luminosidad del objeto.