 Ejercicio 'Luminosidad y brillo'
Ejercicio 'Luminosidad y brillo'
Nivel *
Tiempo necesario :
10 min
La luminosidad corresponde a la potencia total emitida por la estrella. Cuando se considera
esta potencia por unidad de superficie, se le llama potencia de superficie. Se define el
brillo
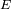
de una estrella como la potencia recibida por unidad de superficie en el límite superior de la atmósfera
terrestre.
1)
La luminosidad real de una estrella de tipo solar es
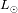
. Deducir el brillo
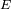
de la estrella vista a una distancia

de la Tierra.
ayuda
solución
2)
Calcular la potencia de superficie recibida en la Tierra de una estrella de tipo solar situada a la misma
distancia de la Tierra que Próxima Centauri, de
paralaje anual

=0.76". Utilizar
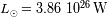
.
solución
3)
Calcular la potencia de superficie
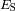
del sol recibida en la Tierra.
ayuda
solución
 Ejercicio 'Magnitud aparente'
Ejercicio 'Magnitud aparente'
Nivel *
Tiempo necesario :
15 min
2)
Dos estrellas tienen brillos aparentes de
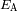
et
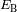
. Expresar la diferencia de magnitud entre los dos objetos.
ayuda
solución
3)
Comparar los flujos de los objetos siguientes : Sol -26.7, J'piter -2.55, estrellas al límite de la detección
del ojo +6, magnitud límite accesible desde el suelo +27.
solución
 Ejercicio 'Capacidades de detección en función del tamaño del receptor'
Ejercicio 'Capacidades de detección en función del tamaño del receptor'
Nivel *
Tiempo necesario :
25 min
En visión nocturna, el diámetro de la pupila mide alrededor de 6 mm, y la magnitud
límite visible del ojo es de
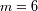
.
Recuérdese que la expresión de

, la magnitud aparente de un objeto es :
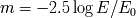
con
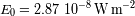
para el dominio visible.
1)
Expresar
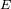
, el flujo radiado (potencia por unidad de superficie) que atraviesa la pupila, en función
de
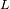
y
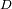
, es decir, la potencia total recibida y el diámetro de la pupila respectivamente.
ayuda
solución
2)
Calcular
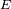
y
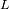
para una estrella de magnitud 6.
solución
3)
Mostrar que con un colector de diámetro
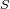
el ojo es capaz de observar magnitudes de hasta :
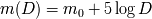
con
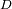
en metros. Identificar
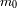 solución
solución
5)
¿Cómo se procede para observar objetos con magnitud superior?
solución
 Ejercicio 'Contar la estrellas'
Ejercicio 'Contar la estrellas'
Nivel *
Tiempo necesario :
20 min
El objetivo del ejercicio es contar las estrellas en función de la magnitud. Para ello,
se suponen dos hipótesis :
- Todas las estrellas tienen la misma magnitud absoluta,
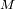
.
- La repartición de las estrellas en torno al Sol es uniforme,

.
1)
Determinar la magnitud aparente de una estrella a una distancia
 ayuda
solución
ayuda
solución
2)
Contar el numero de estrellas
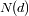
en una esfera de radio

alrededor del Sol.
ayuda
ayuda
solución
3)
Utilizando las dos relaciones anteriormente establecidas, demostrar que el número de estrellas visibles
hasta la magnitud

sigue :
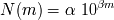
Identificar el coeficiente
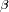
del exponente.
ayuda
ayuda
solución
4)
Estimar

, sabiendo que se cuentan aproximadamente 6000 estrellas a ojo descubierto, es decir, estrellas
con

inferior a 6.
solución
¿Este resultado está de acuerdo con el
número de estrellas
más brillantes que la magnitud 0?
solución

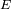 de una estrella como la potencia recibida por unidad de superficie en el límite superior de la atmósfera
terrestre.
de una estrella como la potencia recibida por unidad de superficie en el límite superior de la atmósfera
terrestre.
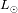 . Deducir el brillo
. Deducir el brillo
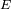 de la estrella vista a una distancia
de la estrella vista a una distancia
 de la Tierra.
ayuda
solución
de la Tierra.
ayuda
solución
 =0.76". Utilizar
=0.76". Utilizar
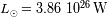 .
.
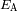 et
et
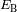 . Expresar la diferencia de magnitud entre los dos objetos.
ayuda
solución
. Expresar la diferencia de magnitud entre los dos objetos.
ayuda
solución
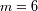 .
.
 , la magnitud aparente de un objeto es :
, la magnitud aparente de un objeto es :
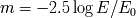
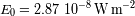 para el dominio visible.
para el dominio visible.
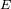 , el flujo radiado (potencia por unidad de superficie) que atraviesa la pupila, en función
de
, el flujo radiado (potencia por unidad de superficie) que atraviesa la pupila, en función
de
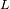 y
y
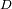 , es decir, la potencia total recibida y el diámetro de la pupila respectivamente.
ayuda
solución
, es decir, la potencia total recibida y el diámetro de la pupila respectivamente.
ayuda
solución
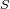 el ojo es capaz de observar magnitudes de hasta :
el ojo es capaz de observar magnitudes de hasta :
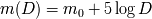
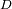 en metros. Identificar
en metros. Identificar
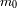 solución
solución
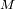 .
.
 .
.
 sigue :
sigue :
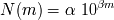
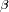 del exponente.
ayuda
ayuda
solución
del exponente.
ayuda
ayuda
solución
 , sabiendo que se cuentan aproximadamente 6000 estrellas a ojo descubierto, es decir, estrellas
con
, sabiendo que se cuentan aproximadamente 6000 estrellas a ojo descubierto, es decir, estrellas
con
 inferior a 6.
solución
inferior a 6.
solución