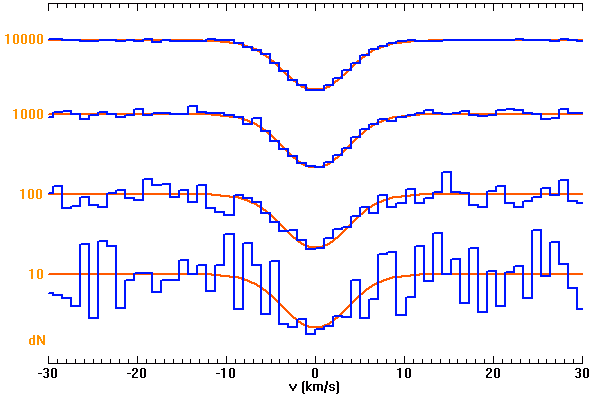
Simulation de la détection d'une raie, en fonction du nombre de photoélectrons dN détectés par intervalle spectral, en supposant la détection limitée par le seul bruit de photons. L'échelle spectrale est donnée en vitesse.
Crédit :
ASM
Bruit de photons et photodétection
Une bonne détection, par exemple l'identification d'une raie spectrale, nécessite l'enregistrement d'un nombre suffisant de photoélectrons, afin que la statistique d'arrivée des photons, de type poissonnien, n'empêche pas la détection.
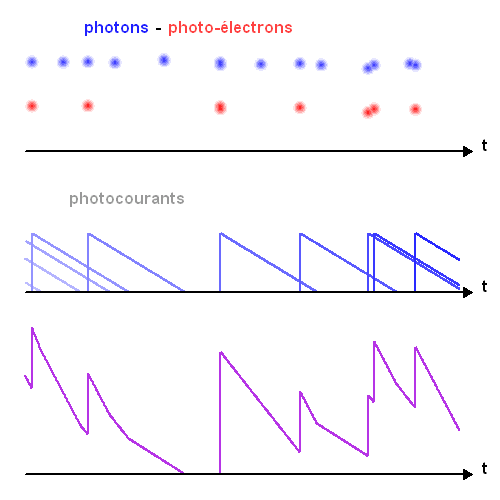
Distribution en fonction du temps de
l'arrivée de photons, des photoélectrons créés et du photocourant résultant. Les photons (points bleus) n'arrivent pas à intervalles de temps réguliers. Seuls un certain nombre d'entre eux donnent naissance à des photoélectrons (points rouges). Le photocourant total (bleu) résulte de la somme des contributions individuelles (couleur variable).
Crédit :
ASM
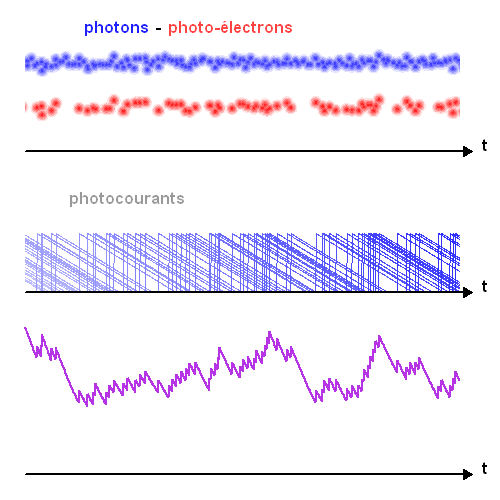
Distribution en fonction du temps de
l'arrivée de photons, des photoélectrons créés et du photocourant résultant. Les photons (points bleus) n'arrivent pas à intervalles de temps réguliers. Seuls un certain nombre d'entre eux donnent naissance à des photoélectrons (points rouges). Le photocourant total (bleu) résulte de la somme des contributions individuelles (couleur variable).
Crédit :
ASM
Photons et photoélectrons
Le bruit de photons est en fait un bruit... de photoélectrons.
L'arrivée dispersée des photons, conjuguée à la conversion aléatoire d'un photon en photoélectron, construisent la statistique de création de photoélectrons, qui dépend bien sûr du nombre de photons.
 Prérequis
Prérequis
Statistique de Poisson : le bruit de photons obéit à la statistique de Poisson.
 Objectifs
Objectifs
Evaluer le bruit et le rapport signal à bruit du bruit de photons.
Statistique de Poisson
La statistique d'arrivée des photons est poissonnienne, vu que les photons sont par définition des quanta d'énergie.
Lorsque l'on attend 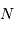 photons par intervalle de temps, la valeur moyenne observée est ...
photons par intervalle de temps, la valeur moyenne observée est ... 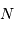 et sa fluctuation autour de cette valeur moyenne vaut
et sa fluctuation autour de cette valeur moyenne vaut 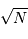 .
.
Il s'ensuit un rapport signal à bruit déterminé par le flux de photons égal à :
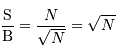
Ce rapport signal à bruit croît avec la racine carrée du nombre de photons collectés.
Photoélectrons
Les photons que l'on observe sont le plus souvent traduits par le détecteurs en photoélectrons, qui suivent la même statistique que les photons, à un facteur de rendement près inférieur à l'unité.
Avec 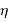 le rendement, le nombre de photoélectrons détectés vaut en fonction du nombre de photons incidents sur le détecteur :
le rendement, le nombre de photoélectrons détectés vaut en fonction du nombre de photons incidents sur le détecteur :
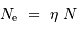
Le bruit de photoélectrons et le rapport signal à bruit résultant valent en pratique 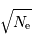 .
.
 Le projet COROT
Le projet COROT
Difficulté : ☆
Temps : 20 min
Question 1)
En supposant que le rendement de la chaîne de détection vaut l'unité, combien de photons doivent être enregistrés pour que le bruit de photons permette une détection à 1 ppm
Avec 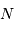 photons, le rapport signal à bruit du bruit de photons vaut
photons, le rapport signal à bruit du bruit de photons vaut 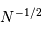 .
.
Question 2)
Le rendement de la chaîne de détection est de 25% seulement. Par quel facteur doit on corriger le nombre de photons à collecter.
Avec 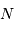 photons, on obtient seulement
photons, on obtient seulement 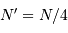 photoélectrons.
photoélectrons.
Question 3)
Le nombre de photons requis est collecté en 5 jours. En déduire le nombre de photons accumulés en une pose élémentaire de 1 minute, et la performance atteinte sur une pose élémentaire.
1 jour = 86400 s = 1440 min
 Au photon près
Au photon près
Difficulté : ☆
Temps : 20 min
La figure ci-jointe représente la courbe de lumière de l'étoile HD 49933, l'une des cibles principales du satellite CoRoT. Le signal stellaire est composé de multiples signaux (activité, oscillations...) et bien sûr du bruit de photons. On admet que celui-ci domine à haute fréquence.
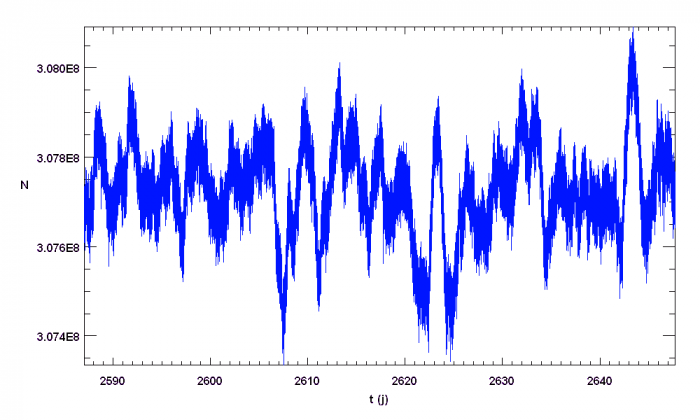
Courbe de lumière de l'étoile HD 49933. Nombre de photo-électrons collectés par seconde en fonction du temps.
Crédit :
ASM/CNES
Question 1)
Estimer l'amplitude totale du bruit du signal stellaire.
[1 points]
Repérer un intervalle de temps où le signal n'évolue pas à basse fréquence, et mesurer l'amplitude crête à crête.
Question 2)
Estimer l'écart-type du bruit
[1 points]
Revoir les propriétés du bruit poissonnien.
Question 3)
Montrer que le bruit mesuré est du même ordre de grandeur que le bruit de photons.
[1 points]



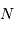 photons par intervalle de temps, la valeur moyenne observée est ...
photons par intervalle de temps, la valeur moyenne observée est ... 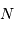 et sa fluctuation autour de cette valeur moyenne vaut
et sa fluctuation autour de cette valeur moyenne vaut 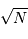 .
.
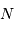 photons, est
photons, est 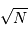 .
.
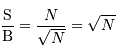
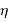 le rendement, le nombre de photoélectrons détectés vaut en fonction du nombre de photons incidents sur le détecteur :
le rendement, le nombre de photoélectrons détectés vaut en fonction du nombre de photons incidents sur le détecteur :
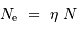
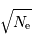 .
.
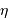 le rendement du détecteur. Le rapport signal à bruit varie comme
le rendement du détecteur. Le rapport signal à bruit varie comme 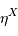 avec
avec 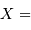 :
:
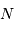 photons, le rapport signal à bruit du bruit de photons vaut
photons, le rapport signal à bruit du bruit de photons vaut 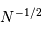 .
.
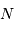 photons, on obtient seulement
photons, on obtient seulement 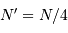 photoélectrons.
photoélectrons.

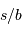 et la performance requise sont tous deux exprimés dans le même système d'unité relative. Le nombre
et la performance requise sont tous deux exprimés dans le même système d'unité relative. Le nombre 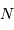 de photons doit donc vérifier :
de photons doit donc vérifier :
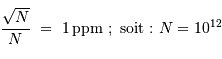
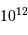 photons pour atteindre la sensibilité requise.
photons pour atteindre la sensibilité requise.
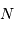 photons, on obtient seulement
photons, on obtient seulement 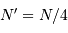 photoélectrons. L'égalité précédente doit donc être vérifiée par
photoélectrons. L'égalité précédente doit donc être vérifiée par 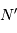 et non par
et non par 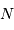 . Il faut donc collecter
. Il faut donc collecter 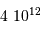 photons.
photons.
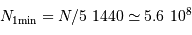
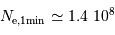 photo-électrons), la performance devient
photo-électrons), la performance devient 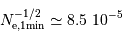 .
.