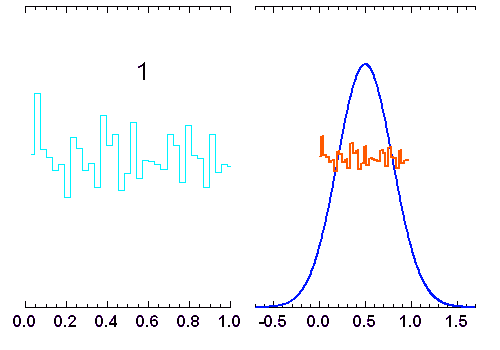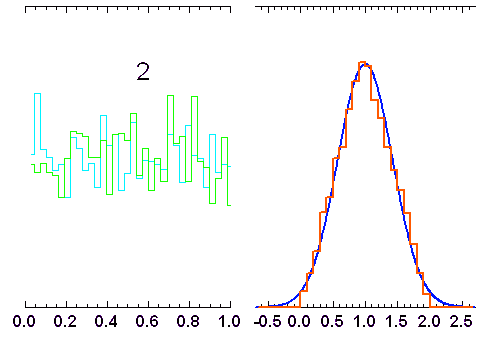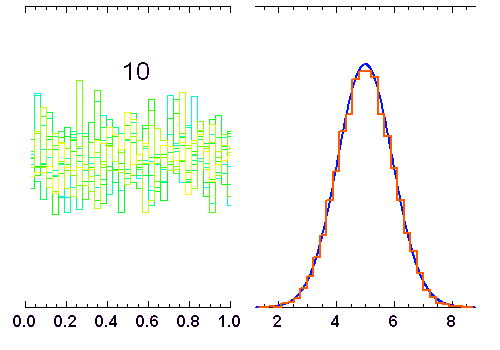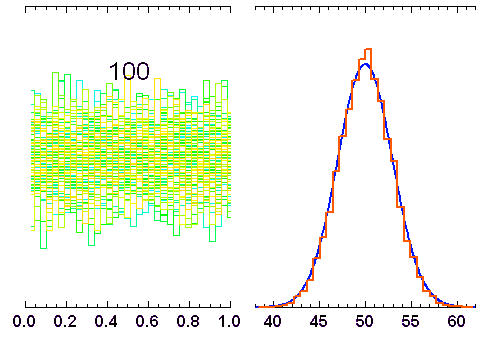

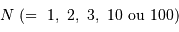 variables indépendantes, obéissant à une loi de distribution uniforme (entre 0 et 1). Lorsque
variables indépendantes, obéissant à une loi de distribution uniforme (entre 0 et 1). Lorsque 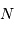 augmente, la distribution tend vers une loi gaussienne de moyenne
augmente, la distribution tend vers une loi gaussienne de moyenne 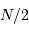 et écart type
et écart type 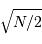 (courbe rouge). Pour
(courbe rouge). Pour 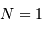 , la distribution reste bien sûr uniforme,
pour
, la distribution reste bien sûr uniforme,
pour 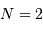 elle garde une allure triangulaire.
elle garde une allure triangulaire.