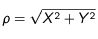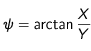Un peu d'astrométrie solaire
Auteur: Carine Briand
- Introduction
- Coordonnées rectangulaires (ou cartésiennes héliocentriques)
- Coordonnées héliographiques
- Définition
- Définir l'origine des longitudes
- Exercice
- Orientation des axes
- Angles de variation d'orientation
- Exercice
- La Longitude absolue
- Exercice
- Exercice
- Résumé
- Système héliocentrique-radial
- Rotation de Carrington
- Changement de coordonnées
- Introduction
- Héliographiques - cartésiennes
- Cartésiennes - Radiales
- Exercice
Introduction
 Introduction
Introduction
La position du Soleil est définie par l'ascension droite et la déclinaison de son centre, comme pour toute étoile (voir chapitre Mécanique Céleste, Temps et Calendriers). Cependant, le Soleil nous offre des détails beaucoup plus précis qu'aucune autre étoile : des détails de l'ordre de 70 km sont maintenant accessibles depuis des télescopes terrestres. Il est donc nécessaire de définir des systèmes de coordonnées qui permettent de repérer sans équivoque ces structures.
Définir un système de coordonnées pour le Soleil n'est cependant pas aussi simple que cela peut paraître. La vitesse de rotation du Soleil varie avec la latitude, et aucun point fixe (et de durée de vie suffisante) ne peut servir de repère puisque le Soleil est gazeux. D'autre part, le Soleil est une sphère : la troisième dimension de notre étoile doit être prise en compte. Enfin, les systèmes de référence sont liés à un observateur. Il faudra adapter les repères pour des observations faites par des satellites dont la distance au Soleil serait plus réduite par rapport à un observateur situé sur Terre. SoHO par exemple est un satellite situé au point de Lagrange - environ 1,5 million de kilomètres de la Terre dans la direction du Soleil - qui voit le Soleil 1% plus gros qu'un observateur sur Terre. Par la suite, nous considèrerons cependant uniquement le point de vue d'un observateur au sol.
Coordonnées rectangulaires (ou cartésiennes héliocentriques)
Définition
La première idée est de repérer une structure par ses coordonnées rectangulaires (X,Y,Z) sur disque projeté sur le plan du ciel (voir figure).
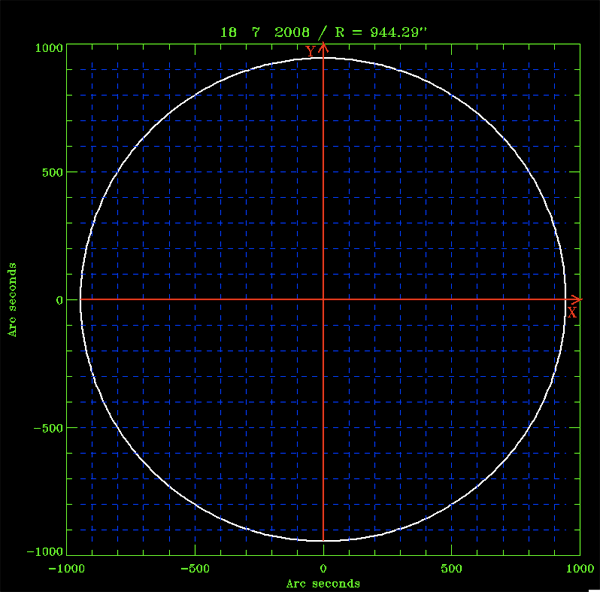
Illustration du système cartésien - héliocentrique. La date et le rayon solaire pour ce jour sont indiqués en haut du graphique
Crédit :
C. Briand - Observatoire de Paris
- L'axe X est parallèle à l'équateur solaire et positif vers le bord (le limbe) ouest.
- L'axe Y est parallèle à la direction Nord-Sud solaire et positif vers le Nord solaire.
- L'axe Z est parallèle à la direction Observateur-Soleil et positif vers l'observateur.
Les positions sur les axes X et Y sont comptées en secondes d'arc (sur le ciel) depuis le centre du disque solaire. Les positions sur l'axe Z sont exprimées en kilomètres depuis le centre du Soleil ou en unité de rayon solaire.
Le centre du disque apparent a pour coordonnées (0,0). Ce repère est fixe par rapport au disque apparent du Soleil (il ne tourne pas avec la rotation solaire).
Cependant, ce repérage (X,Y,Z), s'il est commode à un instant donné, présente plusieurs limitations :
- 1. les coordonnées d'une structure changent en permanence ;
- 2. les coordonnées dépendent du point d'observation.
Un autre système de coordonnées est alors préféré : les coordonnées héliographiques.
Coordonnées héliographiques
Définition
Ce système est très semblable au système terrestre de latitude et longitude. Il est défini par rapport au disque apparent du Soleil en lumière blanche (la photosphère).
La latitude héliographique Θ est comptée depuis l'équateur solaire entre -90° au Sud et +90° au pôle Nord solaire.
La longitude héliographique Φ est un peu plus compliquée à compter car il n'existe pas naturellement de référence fixe (comme par exemple le méridien terrestre passant par Greenwich sur Terre).
L'intérêt de ce système de coordonnées est qu'une structure présente sur le disque solaire conservera les mêmes coordonnées pendant des durées relativement longues. Les variations observées seront dues à l'évolution propre de la structure (changement de forme ou mouvement propre sur le disque solaire) et non pas à la seule rotation solaire. Comme les mouvements propres sont généralement plus lents que la rotation solaire, on pourra repérer un groupe sur une plus longue période qu'avec les coordonnées cartésiennes qui changent en permanence.
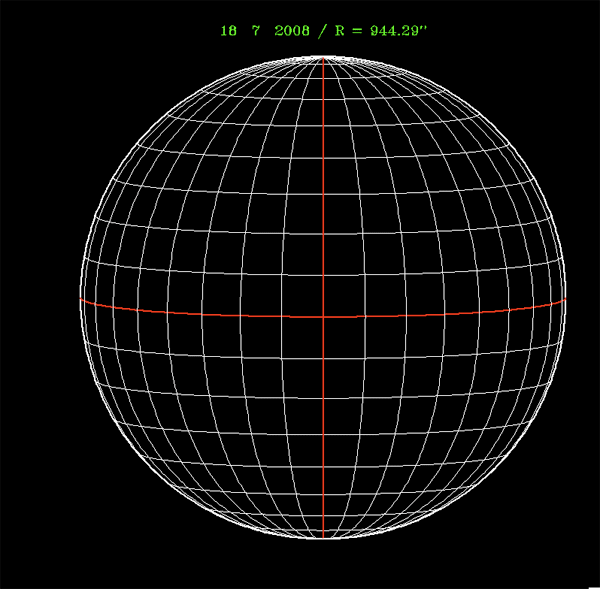
Grille du Soleil en coordonnées héliographiques. Les lignes parallèles à l'équateur (ligne rouge est-ouest) repèrent la latitude. Les lignes passant par les pôles nord-sud sont les méridiens. Le méridien en rouge est le méridien central. Les points sont représentés tous les 10° (aussi bien en longitude qu'en latitude).
Crédit :
C. Briand - Observatoire de Paris
Définir l'origine des longitudes
Une première solution est de définir les longitudes par rapport au méridien central. Le méridien central est la ligne passant par les pôles solaires nord et sud et le centre apparent du disque solaire à un instant donné. Les longitudes sont alors comptées positivement vers le bord solaire Ouest (-90° au bord solaire Est et +90° au bord solaire Ouest).
Attention : on utilise des mesures d'angle, mais 1° de latitude/longitude sur le Soleil ne correspond pas à 1° sur le ciel. Le Soleil tournant sur lui-même, la longitude d'une structure varie à chaque instant (environ 13,2°/jour, déterminé à partir d'une rotation synodique moyenne de 27,2753 j).
Exercice
 Les lignes de longitude héliographique
Les lignes de longitude héliographique
Question 1)
La grille du Soleil en coordonnées héliographiques montre que les lignes de longitude se resserrent près du bord est et ouest. Savez-vous expliquer pourquoi ?
Orientation des axes
Nous ne sommes pas tout à fait au bout de nos peines. En effet, l'orientation des axes propres du Soleil (axe de rotation, équateur) ne sont pas confondus avec les axes X,Y du système héliocentrique cartésien à cause de :
- L'inclinaison de l'axe de rotation de la Terre par rapport au plan de l'écliptique (23,4°);
- L'inclinaison de l'axe de rotation du Soleil par rapport au plan de l'écliptique (7,25°) ;
Par conséquent :
- 1. le centre du disque solaire projeté sur le fond du ciel n'est pas confondu avec l'origine des coordonnées héliographiques,
- 2. l'axe de rotation du Soleil est incliné par rapport au nord céleste,
- 3. le rayon apparent du Soleil varie au cours de l'année.
La figure illustre les inclinaisons apparentes du Soleil au cours de l'année.
Angles de variation d'orientation
Pour tenir compte de ces variations d'orientation, deux nouveaux angles sont nécessaires :
- L'angle
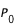 entre le Pôle Nord Céleste et le Pôle Nord Solaire. Il est compté positivement quand le pôle nord solaire est dirigé vers l'est et varie de ±26.3° au cours de l'année;
entre le Pôle Nord Céleste et le Pôle Nord Solaire. Il est compté positivement quand le pôle nord solaire est dirigé vers l'est et varie de ±26.3° au cours de l'année; - L'angle
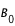 est la latitude héliocentrique du centre apparent du disque solaire. Cet angle est positif quand l'équateur solaire est dirigé vers le Sud céleste. Il varie de ±7.23° au cours de l'année.
est la latitude héliocentrique du centre apparent du disque solaire. Cet angle est positif quand l'équateur solaire est dirigé vers le Sud céleste. Il varie de ±7.23° au cours de l'année.
Le Soleil nous laisse donc voir alternativement ses pôles nord et sud : le pôle sud quand 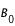 est négatif, le pôle nord quand
est négatif, le pôle nord quand 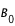 est positif. Pour bien voir l'évolution de tous ces paramètres au cours de l'année, nous vous recommandons d'utiliser cet applet.
est positif. Pour bien voir l'évolution de tous ces paramètres au cours de l'année, nous vous recommandons d'utiliser cet applet.
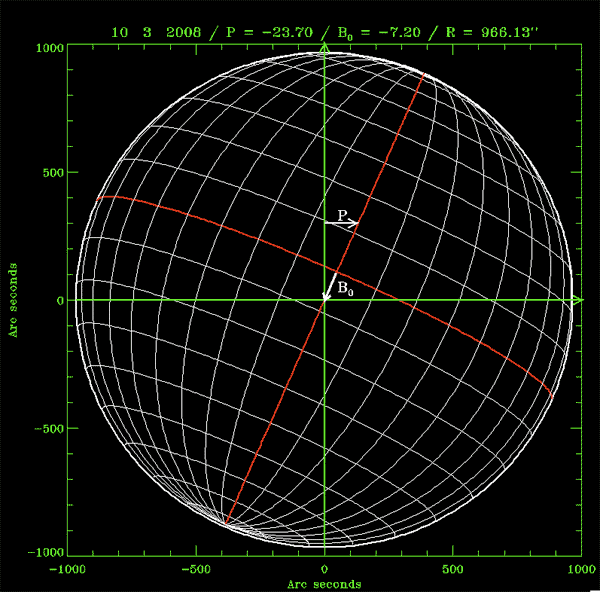
Illustration des angles P et B0. Dans le cas présenté : P = -23,7° et B = -7.2° . Les deux lignes en rouge représentent l'équateur et le méridien central solaire, les lignes en vert représentent les axes X,Y - voir schémas précédents pour plus de détails.
Crédit :
C. Briand - Observatoire de Paris
Exercice
 Détermination des angles P et B0
Détermination des angles P et B0
Question 1)
La figure montre la carte du Soleil du 5/01/2008 et 11/10/2008. Les axes du système cartésien sont dessinés en vert, tandis que les axes du système héliographique sont en rouge. L'Ouest est à droite, le Nord vers le haut.
Donnez une valeur approximative des angles P, B0 pour les deux dates.
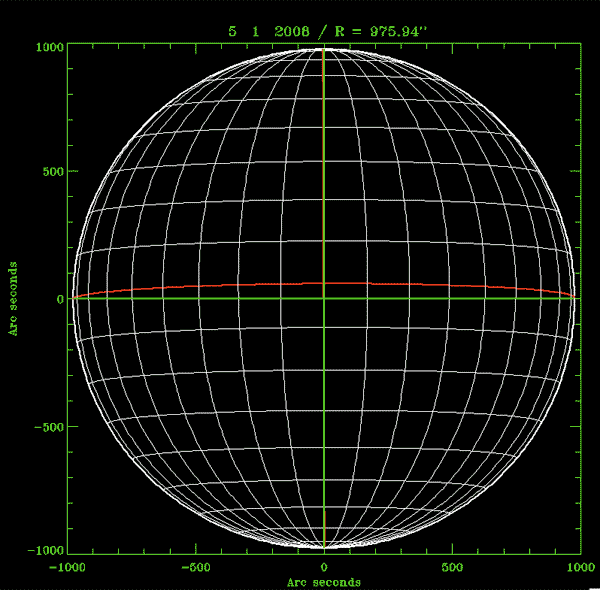
Crédit :
C. Briand - Observatoire de Paris
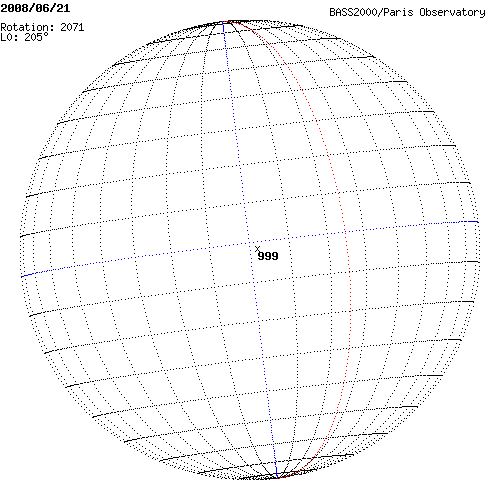
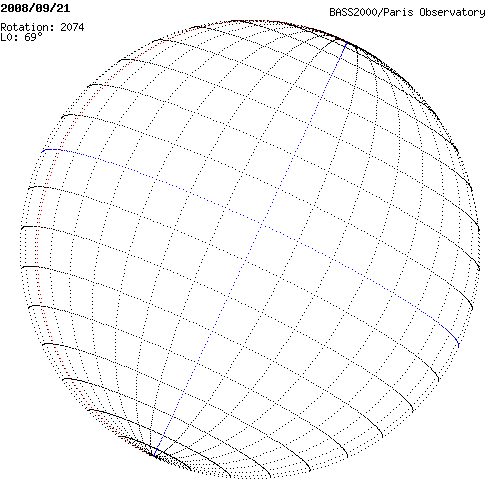
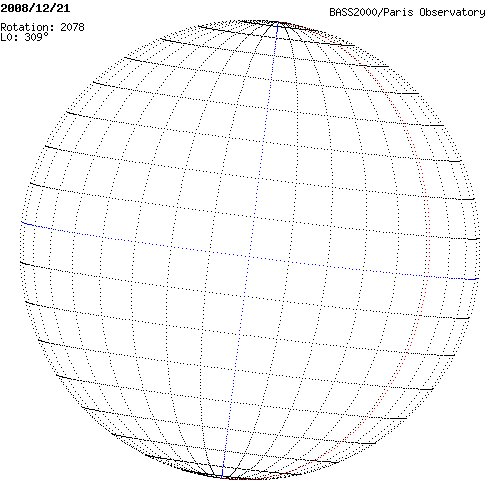
La Longitude absolue
Pour donner une valeur absolue de longitude, on introduit la longitude (absolue) du méridien central L0 à partir d'un méridien de référence.
 Définition
Définition
Le méridien de référence (ϕ= 0°) est défini comme le méridien qui passait par le nœud ascendant de l'équateur solaire à Greenwich à 12h le 1er Janvier 1854.
Ce méridien de référence tourne avec le Soleil. Sa vitesse de rotation se détermine par rapport à une période de rotation sidérale constante de 25,38 jours. La longitude du méridien central décroît ainsi de 360° à 0° à mesure que le méridien de référence se déplace vers l'ouest (rotation solaire).
La longitude du méridien central L0 est donnée par :
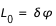
Avec  l'écart en longitude entre le méridien central et le méridien de référence, compté positivement vers le bord ouest du Soleil. (Une autre façon de calculer la longitude du méridien central :
l'écart en longitude entre le méridien central et le méridien de référence, compté positivement vers le bord ouest du Soleil. (Une autre façon de calculer la longitude du méridien central :  pour les structures à l'ouest du méridien de référence et 360° +
pour les structures à l'ouest du méridien de référence et 360° +  pour les méridiens à l'est avec dans ce cas
pour les méridiens à l'est avec dans ce cas 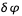 négatif). La figure donne quelques exemples de valeurs de
négatif). La figure donne quelques exemples de valeurs de 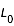 pour différentes dates.
pour différentes dates.
La longitude absolue 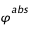 d'une structure sur le disque, connaissant sa longitude relative
d'une structure sur le disque, connaissant sa longitude relative 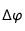 (par rapport au méridien central) et la longitude du méridien central
(par rapport au méridien central) et la longitude du méridien central 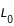 est donnée par :
est donnée par :
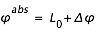
La rotation du Soleil et le déplacement orbital de la Terre sont dans le même sens (dans le sens inverse des aiguilles d'une montre quand on regarde depuis le pôle nord du plan orbital terrestre). Ceci est précieux pour orienter les cartes pendant des observations. Il suffit de couper l'entraînement du moteur d'une monture équatoriale et de laisser défiler le Soleil. La dérive de l'image indiquera la direction est-ouest (sens de rotation de la Terre) et également la direction est-ouest du Soleil.
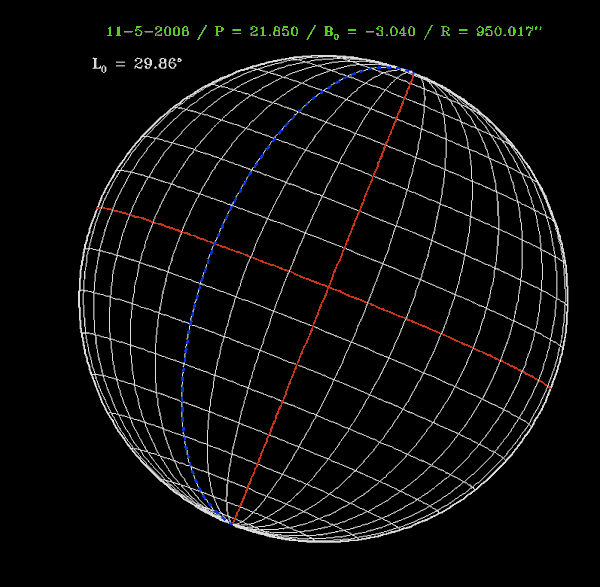
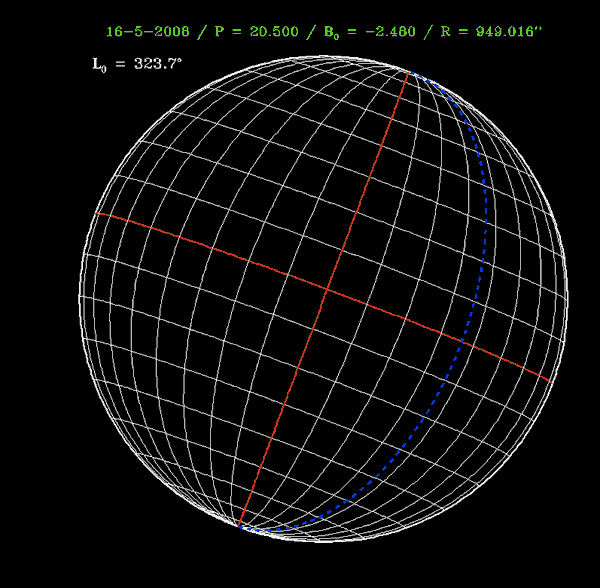
Carte du Soleil en coordonnées héliographiques à deux dates (11 et 16 mai 2008). Le méridien bleu indique la position du méridien de référence (Φ = 0°). La valeur de la longitude du méridien central L0 (dessiné en rouge) est fournie sur chaque carte.
Crédit :
C. Briand - Observatoire de Paris
Exercice
 Longitude du méridien central
Longitude du méridien central
Question 1)
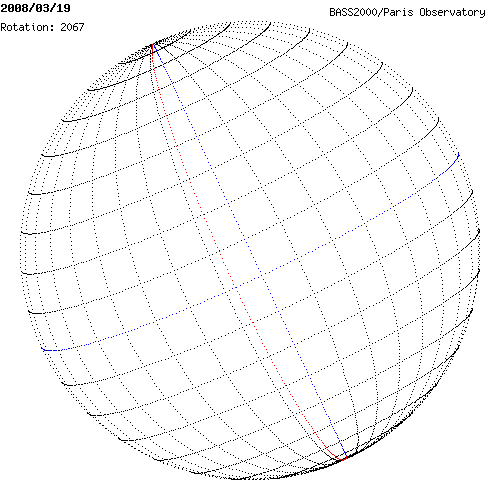
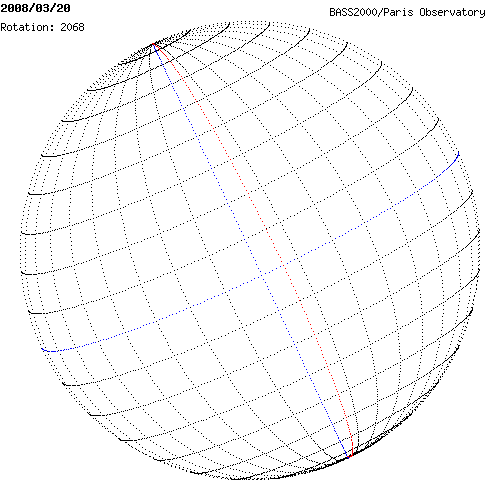
Crédit :
BASS 2000
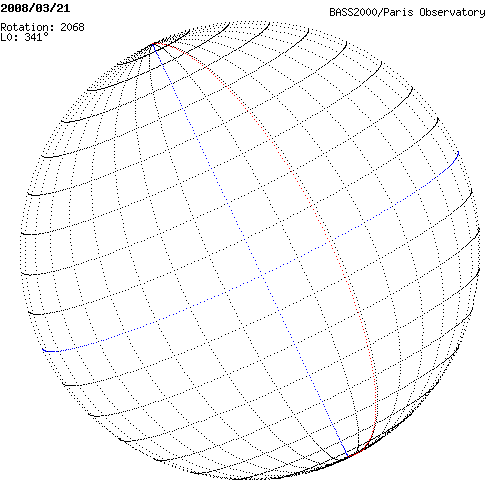
Les deux cartes présentent l'orientation du Soleil les 19 et 20 Mars 2008. Le méridien en bleu est le méridien central, le méridien en rouge est le méridien de référence (Φ = 0°). Les méridiens sont indiqués tous les 10°. L'Ouest est situé vers la droite. Pouvez-vous donner un ordre de grandeur de la longitude du méridien central ?
Exercice
 Coordonnées des taches
Coordonnées des taches
Question 1)
La carte donne la position de toutes les taches ou groupes de taches visibles sur le Soleil le 31/08/2001. Chaque groupe est identifié par un numéro qu'il conservera pendant toute sa vie. Ce numéro NOAA est donné par le National Oceanic and Atmospheric Administration (NOAA).
- 1. Donnez les coordonnées héliographiques (relatives au méridien central) de chaque groupe.
- 2. La longitude du méridien central L0 était de 255°. Déduire les coordonnées absolues de chaque groupe de taches.
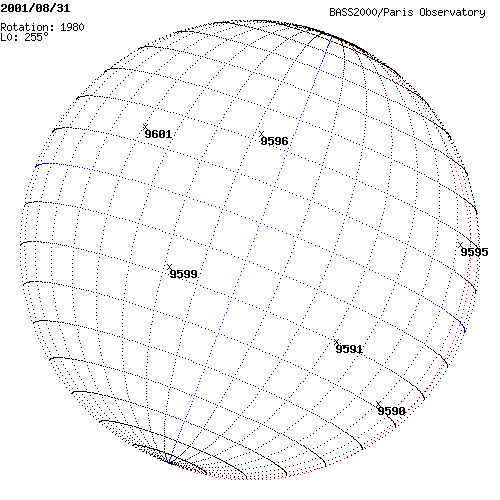
Carte avec la position des taches ou groupes de taches visibles sur le Soleil le 31/08/2001.
Crédit :
BASS 2000 - Observatoire de Paris
Résumé
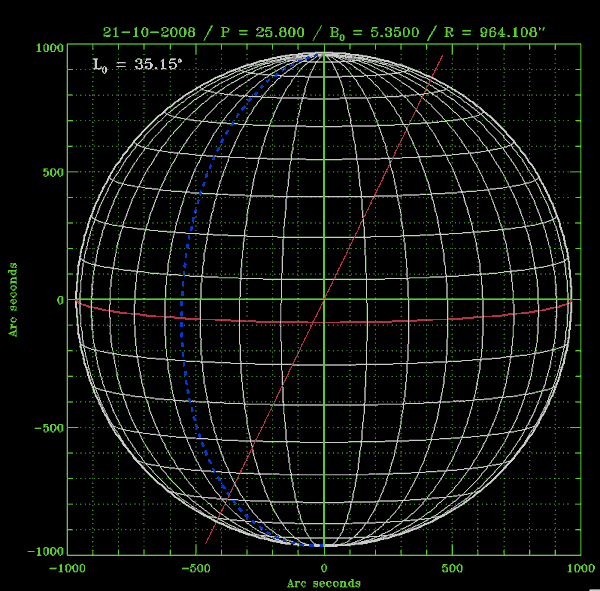
La figure montre l'ensemble des paramètres définis précédemment sur un seul et même graphique :
- pointillés verts : coordonnées X,Y (avec les axes de référence en traits pleins verts)
- ligne rose : direction Nord Céleste
- en rouge l'équateur solaire (le méridien central est confondu avec l'axe Y dans cette représentation)
- Le méridien pointillé bleu : la position du méridien de référence.
Crédit :
C. Briand - Observatoire de Paris
Système héliocentrique-radial
Introduction
 Introduction
Introduction
Nous avons vu que le système héliographique permettait de situer toutes les structures qui apparaissent sur le disque solaire et de les suivre pendant leur transit sur le disque solaire. Mais clairement, il ne peut pas nous aider pour des structures sur le bord sur disque (telles que les protubérances) : latitudes et longitudes ne peuvent pas excéder la taille du disque solaire.
Quand un point d'observation se situe très près du bord solaire, même si les coordonnées héliographiques sont toujours définies, elles sont rarement commodes (car pas assez précises). On utilise alors un troisième système de coordonnées : héliocentrique-radial.
Définition
Le système héliocentrique-radial est défini par :
- ρ : la distance au centre du disque solaire (en unité de seconde d'arc sur le ciel)
- ψ : l'angle entre le pôle nord solaire et le point d'observation. Il est compté positivement vers l'Est solaire
Il n'y a aucune contrainte sur les valeurs des deux paramètres.
Tout comme les coordonnées cartésiennes, les coordonnées d'un point sur le disque changent en permanence. C'est pour cette raison que ce système est préférentiellement utilisé pour les structures hors du Soleil.
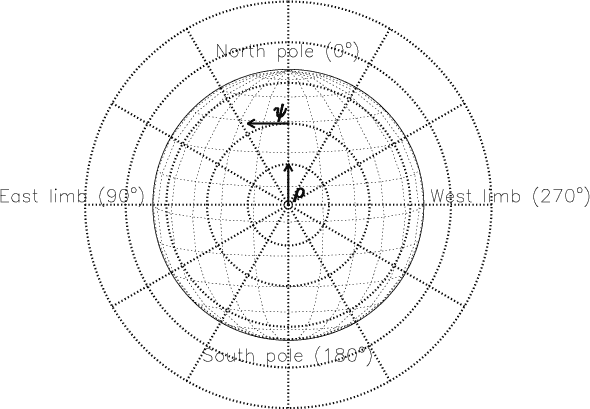
Illustration du système héliographique-radial. "East limb" est le limbe solaire Est.
Crédit :
Thompson, Astronomy & Astrophysics Journal, 2006
Rotation de Carrington
Définition
Le numéro de rotation Carrington indique le nombre de rotations du Soleil, vu depuis la Terre, depuis le 9 Novembre 1853. Cette date ne correspond à rien de particulier du point de vue astronomique. C'est juste le jour où Carrington a commencé ses observations systématiques du Soleil à Greenwich.
Le numéro de rotation Carrington est un nombre entier non nul. Les jours correspondant à une même rotation ont ainsi le même numéro de rotation. Puisque c'est un point de vue de l'observateur terrestre, c'est la rotation synodique du méridien central qui indique la vitesse moyenne de rotation du Soleil (27,2753 jours).
Exercice
 Numéro de rotation
Numéro de rotation
Question 1)
Quel est le numéro de la rotation Carrington du Soleil au 9/11/2008 ? au 12/03/2009 ?
Si besoin est, vous pouvez calculer le jour Julien à partir du site suivant.
Changement de coordonnées
Introduction
 Introduction
Introduction
Nous allons traiter les deux cas les plus usuels de changement de coordonnées. Les formules suivantes ne sont pas à connaître par cœur, mais sont à savoir utiliser.
Héliographiques - cartésiennes
Soient (X,Y) les coordonnées d'un point en coordonnées cartésiennes - héliocentriques (en secondes d'arc sur le ciel), 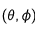 la latitude et longitude (relative),
la latitude et longitude (relative), 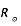 le rayon du Soleil (en secondes d'arc sur le ciel), et P et B les angles d'orientation des axes propres. Nous avons les relations suivantes :
le rayon du Soleil (en secondes d'arc sur le ciel), et P et B les angles d'orientation des axes propres. Nous avons les relations suivantes :
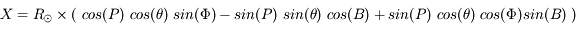
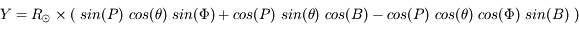
Cartésiennes - Radiales
Le passage des coordonnées cartésiennes (X,Y) aux coordonnées radiales(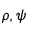 ) se fait par les formules :
) se fait par les formules :
Exercice
 Coordonnées cartésiennes et radiales
Coordonnées cartésiennes et radiales
Question 1)
La figure montre une observation réelle du Soleil. La grille de coordonnées héliographiques a été superposée à cette image de la haute photosphère. Déterminez les coordonnées héliographiques (relatives et absolues) de toutes les taches. En déduire les coordonnées cartésiennes et radiales.

Crédit :
Observatoire de Paris
Réponses aux exercices
pages_astrometrie-solaire/so-exo-carrington.html
Exercice
'Numéro de rotation'
 Introduction
Introduction

 entre le Pôle Nord Céleste et le Pôle Nord Solaire. Il est compté positivement quand le pôle nord solaire est dirigé vers l'est et varie de
entre le Pôle Nord Céleste et le Pôle Nord Solaire. Il est compté positivement quand le pôle nord solaire est dirigé vers l'est et varie de 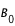 est la latitude héliocentrique du centre apparent du disque solaire. Cet angle est positif quand l'équateur solaire est dirigé vers le Sud céleste. Il varie de
est la latitude héliocentrique du centre apparent du disque solaire. Cet angle est positif quand l'équateur solaire est dirigé vers le Sud céleste. Il varie de 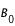 est négatif, le pôle nord quand
est négatif, le pôle nord quand 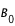 est positif. Pour bien voir l'évolution de tous ces paramètres au cours de l'année, nous vous recommandons d'utiliser
est positif. Pour bien voir l'évolution de tous ces paramètres au cours de l'année, nous vous recommandons d'utiliser 


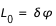
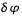 l'écart en longitude entre le méridien central et le méridien de référence, compté positivement vers le bord ouest du Soleil. (Une autre façon de calculer la longitude du méridien central :
l'écart en longitude entre le méridien central et le méridien de référence, compté positivement vers le bord ouest du Soleil. (Une autre façon de calculer la longitude du méridien central : 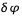 pour les structures à l'ouest du méridien de référence et 360° +
pour les structures à l'ouest du méridien de référence et 360° + 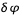 pour les méridiens à l'est avec dans ce cas
pour les méridiens à l'est avec dans ce cas 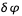 négatif). La
négatif). La 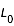 pour différentes dates.
pour différentes dates.
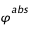 d'une structure sur le disque, connaissant sa longitude relative
d'une structure sur le disque, connaissant sa longitude relative 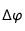 (par rapport au méridien central) et la longitude du méridien central
(par rapport au méridien central) et la longitude du méridien central 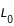 est donnée par :
est donnée par :
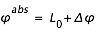







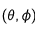 la latitude et longitude (relative),
la latitude et longitude (relative), 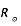 le rayon du Soleil (en secondes d'arc sur le ciel), et P et B les angles d'orientation des axes propres. Nous avons les relations suivantes :
le rayon du Soleil (en secondes d'arc sur le ciel), et P et B les angles d'orientation des axes propres. Nous avons les relations suivantes :
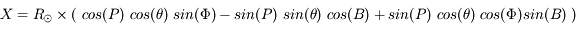
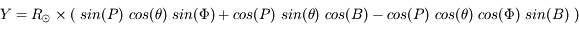
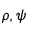 ) se fait par les formules :
) se fait par les formules :