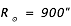Changement de coordonnées : Page pour l'impression

Introduction

Nous allons traiter les deux cas les plus usuels de changement de coordonnées. Les formules suivantes ne sont pas à connaître par cœur, mais sont à savoir utiliser.

Héliographiques - cartésiennes

Soient (X,Y) les coordonnées d'un point en coordonnées cartésiennes - héliocentriques (en secondes d'arc sur le ciel), 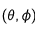$(\theta,\phi)$ la latitude et longitude (relative), 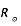R_soleil le rayon du Soleil (en secondes d'arc sur le ciel), et P et B les angles d'orientation des axes propres. Nous avons les relations suivantes :

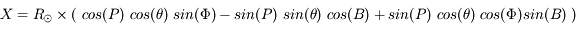
$X = R_\odot\times(~cos(P)~cos(\theta)~sin(\Phi) - sin(P)~sin(\theta)~cos(B) + sin(P)~cos(\theta)~cos(\Phi)sin(B)~)$

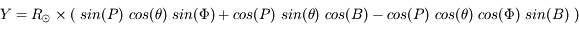
$Y = R_\odot\times(~sin(P)~cos(\theta)~sin(\Phi) + cos(P)~sin(\theta)~cos(B) - cos(P)~cos(\theta)~cos(\Phi)~sin(B)~)$

Cartésiennes - Radiales

Le passage des coordonnées cartésiennes (X,Y) aux coordonnées radiales(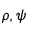 $\rho,\psi$ ) se fait par les formules :

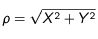
$\rho = \sqrt{X^2+Y^2}$
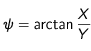
$\psi = \arctan{X \over Y}$

Exercice

Coordonnées cartésiennes et radiales

Question 1)

La figure montre une observation réelle du Soleil. La grille de coordonnées héliographiques a été superposée à cette image de la haute photosphère. Déterminez les coordonnées héliographiques (relatives et absolues) de toutes les taches. En déduire les coordonnées cartésiennes et radiales.

R_soleil=900"

Crédit : Observatoire de Paris